17.1. Для работы с очередью, т.е. последовательностью элементов, в которую элементы всегда добавляются коней:, а удаляются из начала («первым пришел—первым ушел»), нужны обычно следующие – операции:
ОЧИСТОЧ(Q) —создать пустую очередь Q (очистить очередь);
ПУСТОЧ(Q)- проверить является ли очередь Q пустой;
ВОЧЕРЕДЬ(Q,х)- добавитьв конец очереди Q элемент;
ИЗОЧЕРЕДИ(Q,х)- удалитьиз очереди Q первый элемент, присвоив его параметру х.
Требуется для каждого из указанных ниже представлений очереди описать на Паскале соответствующий тип очередь, считая, что все элементы очереди имеют некоторый тип ТЭО, и реализовать в виде процедур или функций перечисленные операции над очередью (если операция по тем или иным причинам не может быть выполнена, следует передать управление некоторой процедуре ОШИБKA(k), считая ее уже описанной, где к —номер ошибки: 1—переполнение очереди, 2—исчерпание очереди).
Представление очереди (n —целая константа>1):
а)* для каждой очереди отводится свой массив из п компонент типа ТЭО, в котором элементы очереди занимают группу соседних компонент, индексы первой и последней из которых запоминаются (рис. 16, а); при этой, когда очередь достигает правого края массива, все ее элементы сдвигаются к левому краю;
б) аналогичное представление, но массив как бы склеивается в кольцо, поэтому если очередь достигает правого края массива, то новые элементы записываются в начало массива (рис. 16,б);
в) для каждой Очереди создается свой однонаправленный список из элементов типа ТЭ0 при этом запоминаются ссылки на первое и последнее звенья списка (рис. 16, в).
17.2. Используя очередь (считать уже описанными тип очередь при подходящем типе ТЭО, функцию ПУСТОЧ и процедуры ОЧИСТОЧ, ВОЧЕРЕДЬ и ИЗОЧЕРЕДИ—cм. 17.1 ), решить следующую задачу (решение описать в виде процедуры).
a)*typeFR=file of real;
За один просмотр файла f типа FR и без использования дополнительных файлов напечатать элементы файла f в следующем порядке: сначала—все числа, меньшие а, затем—все числа из отрезка [a,b], и наконец—все остальные числа, сохраняя исходный взаимный порядок в каждой из этих трех групп чисел (а и b —заданные числа, а<b).
б) Содержимое текстового файла f, разделенное на строки, переписать в текстовый файл g перенося при этом в конец каждой строки все входящие в нее цифры (с сохранением исходного взаимного порядка как среди цифр, так и среди остальных литер строки);
в) type имя = (Анна,...,Яков);
дети= array [имя,имя] of boolean;
потомки=file of имя;
Считая заданными имя И и массив Д типа дети (Д[х,у]=иие, если человек по имени y является ребенком человека по имени х), записать в файл П типа потомки имена всех потомков человека с именем И в следующем порядке: сначала—имена всех его детей, затем—всех его внуков, затем всех правнуков и т. д.
17.3. Для работы со стеком, т. е. последовательностью элементов, в которой элементы всегда добавляются в конец и удаляются из конца («последним пришел —первым ушел») нужны обычно следующие операции:
ОЧИСТЕK(S)— создать пустой стек S (очистить стек);
ПУCTEK(S)— проверить, является ли стек S пустым;
BCTEK(S,x)— добавить в конец стека S элемент х:
ИЗСТЕКA(S,x)— удалить из очереди S последний элемент, присвоив его параметру х.
Требуется для каждого из указанных ниже представлений стека описать на Паскале соответствующий тип стек, считая, что все элементы стека имеют некоторый тип ТЭС, и реализовать в виде процедур или функций перечисленные операции над стеком (если операция по тем или иным причинам невыполнима, следует передать управление некоторой процедуре ошибка(k), считая ее уже описанной, где k —номер ошибки: 1—переполнение стека 2— исчерпание стека).
Представление стека (п — целая константа>1)
а) для каждого стека отводится свой массив из п компонент типа ТЭС, в начале которого располагаются элементы стека, при этом запоминается индекс компоненты массива, занятой последним элементом стека (рис. 17, а);
б) для каждого стека создается свой однонаправленный список, в котором элементы стека располагаются в обратном порядке (рис. 17,б).
17.4. Используя стек (считать уже описанными тип стек при TЭC=char, функцию ПУСТЕК и процедуры ОЧИСТЕК, ВСТЕК и ИЗСТЕКА— см. 17.3), решить следующую задачу (решение описать в виде процедуры или функции).
а) Напечатать содержимое текстового файла t, выписывая литеры каждой его строки в обратном порядке.
б) Проверить, является ли содержимое текстового файла t правильной записью формулы следующего вида:
<формула>::=<терм> | <терм>+<формула>|
<терм>—<формула>
<терм>::=<имя>|(формула)|[<формула>]|
{<формула>}
<имя>::=x|y|z
в)* В текстовом файле f записана без ошибок формула следующего вида:
<формула>::=<цифра> \ М<формула>,<формула>)
m(<формула>,< формула >)
<цифра>::= 0|1|2|3|4||5|6|7|8|9
где М обозначает функцию max, a m—mln.
Вычислить (как целое число) значение данной формулы (например, М(5,m(6,8)) →6).
г) В текстовом файле LOG записано без ошибок логическое выражение (ЛВ) в следующей форме:
<ЛВ>::=true|falsе|(┐ЛВ>)|(<ЛВ>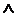 
< ЛВ >)|(<ЛВ> 
< ЛВ >)
где знак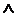и ┐, и обозначают соответственно отрицание, конъюнкцию и дизъюнкцию.
Вычислить (как boolean) значение этого выражения.
17.5. Используя очередь и или стек (считать уже описанными их типы и операции над ними—см. 17.1 и 17.3), решить следующую задачу (решение описать в виде процедуры).
В текстовом файле t записан текст, сбалансированный по круглым скобкам:
<текст>::= <пусто>| <элемент> <текст>
<элемент>::=<буква> | <текст>
Требуется для каждой пары соответствующих открывающей и закрывающей скобок напечатать номера их позиций в тексте, упорядочив пары номеров в порядке возрастания номеров позиций:
а) закрывающих скобок;
б) открывающих скобок.
Например, для текста А+(45—F(X)*(B—С)) надо напечатать:
а)8 10; 12 16; 3 17;
б)3 17; 8 10; 12 16.
17.6. Под «выражением» будем понимать конструкцию следующего вида:
<выражение>::=<терм>|
<терм><знак+—><вьгражение>
<знак+—>::= +|—
<терм>::=<множитель> |<множитель>*<терм>
<множитель>::=<чнсло> | <переменная> | (<выражевие>) |
<множитель> ↑ <число>
<число>::=<цифра>
<переменная>::=<буква>
где знак ↑ обозначает операцию возведения в степень.
Постфиксной формой еаписи выражения а∆b называется запись, в которой знак операции размещен за операндами! аb∆. Примеры:
a-b →ab-
a*b+c →ab*c+ т.е. (ab*)c+)
a*(b+c) →abc+* т.е. (a(bc+)*)
a+b↑c↑d*e →abc↑d↑e*+
а) Описать функцию value(postfix), которая вычисляет как целое число значение выражения (без переменных), записанного в постфиксной форме в текстовом файле postfix.
Использовать следующий алгоритм вычисления. Выражение просматривается слева направо. Если встречается операнд (число), то его значение (как целое) заносится в стек, а если встречается знак операции, то из.стека извлекаются два последних элемента (это операнды данной операции), над ними выполняется операция и ее результат записывается в стек. В конце концов в стеке останется только одно число—значение всего выражения.
б) Описать процедуру translate(infix,postfix), которая переводит выражение, записанное в обычной (инфиксной) форме в текстовом файле infix, в постфиксную форму и в таком виде записывает его в текстовый файл postfix.
Использовать следующий алгоритм перевода. В стек записывается открывающая скобка, и выражение просматривается слева направо. Если встречается операнд (число или переменная), то он сразу переносится в файл postfix. Если встречается открывающая скобка, то она. заносится в стек, а если встречается закрывающая скобка, то из стека извлекаются находящиеся там знаки операций до ближайшей открывающей скобки, которая также удаляется из стека, и все эти знаки (в порядке их извлечения) записываются в файл postfix. Когда же встречается знак операции, то из конца стека извлекаются (до ближайшей скобки, которая сохраняется в стеке) знаки операций, старшинство которых больше или равно старшинству дайной операции, и они записываются в файл postfix, после чего рассматриваемый знак заносится в стек. В завключение выполняются такие же действия, как если бы встретилась закрывающая скобка.
в) Описать (нерекурсивную) процедуру lnjixprint(postfix), которая печатает в обычной (инфиксной) форме выражение, записанное в постфиксной форме в текстовом файле postfix. (Лишние скобки желательно не печатать.)
В упражнениях 17.7—17.14 использовать двоичные деревья (рис. 18) при следующем их описаним
type ТЭД=...; {тип элементов дерева} дерево=^веришна;
вершина =record элем:ТЭД;
лев,прав:дерево
end;
В этих упражнениях Т, Т1 и Т2 обозначают деревья, а Е — величину типа ТЭД.
17.7. Используя очередь или стек (считать уже описанными их типы и операции над ними—см. 17.1и 17.3), описать процедуру или функцию, которая:
а) присваивает параметру Е элемент из самого левого листа непустого дерева Т (лист—вершина, из которой не выходит ни одной ветви);
б)* определяет число вхождений элемента Е в дерево Т;
в) вычисляет среднее арифметическое всех элементов непустого дерева Т (ТЭД=rеа1)
г) заменяет в дереве Т все отрицательные элементы на их абсолютные величины (ТЭД=rеа1);
д) меняет местами максимальный и минимальный элементы непустого дерева 7, все элементы которого различны (ТЭД=rеа1);
с) печатает элементы из всех листьев дерева Т (ТЭД=reаl)
ж)* печатает все элементы дерева Т по уровням! сначала—из корня дерева, затем (слева направо)—из вершин, дочерних по отношению к корню, затем (также слева направо)—из вершин, дочерних по отношению к этим вершинам, и т. д. (ТЭД=integer);
з) находит в непустом дереве Т длину (число ветвей) пути от корня до ближайшей вершины с элементом Е; если Е не входит в Т, за ответ принять —1;
и) подсчитывает число вершин на n -ом уровне непустого дерева Т (корень считать вершиной 0-го уровня).
17.8. Описать рекурсивную функцию или процедуру, которая:
а) определяет, входит ли элемент Е в дерево Т
б)* определяет число вхождений элемента Е в дерево T;
в) вычисляет сумму элементов непустого дерева Т (ТЭД=rеа1);
г) находит величину наибольшего элемента непустого дерева Т (ТЭД=rеа1);
д) печатает элементы из всех листьев дерева Т (ТЭД= char);
е)* определяет максимальную глубину непустого дерева T, т. е. число ветвей в самом длинном из путей от корня дерева до листьев;
ж) подсчитывает число вершин на n-ом уровне непустого дерева Т (корень считать вершиной 0-го уровня).
17.9. Рекурсивно и нерекурсивно описать логическую функцию equal(T1T2), проверяющую на равенство деревья Т1 и Т2.
17.10 *. Описать процедуру сору(Т,Т1) которая строит T1—копию дерева Т.
17.11. Описать процедуру create(T,n), где n—положительное целое число, которая строит Т —дерево, показанное на рис. 19.
17.12. Описать логическую функцию same(T)t определяющего, есть ли в дереве Т хотя бы два одинаковых элемента.
17.13. Формулу вида:
<формула>::=<терминал> |
(<формула><знак><формула>)
<знак>::=+|—|*
<тернинал>::=0|1 |2|3|4 |5 | 6|7|8 |9
можно представить в виде двоичного дерева («дерева-формулы») с ТЭД=char согласно следующим правилам:формула из одного терминала (цифры) представляется; деревом из одной вершины с этим терминалом, а формула вида:
(f1 s f2)—деревом, в котором корень—это знак s, а левое и правое поддеревья — это соответствующие представления формул, f1 и f2. (На рис. 20 показано дерево-формула, соответствующее формуле (5*(3+8)).)
Описать рекурсивную функцию или процедуру, которая:
a) вычисляет (как целое число) значение дерева-формулы Т;
б) по формуле из текстового файла f строит соответствующее дерево-формулу Т;
b) печатает дерево-формулу Т в виде соответствующей формулы;
г) проверяет, является ли двоичное дерево Т деревом- формулой..
17.14. Пусть в дереве-формуле (см. упр. 17.13)в качестве терминалов используются не только цифры, но и буквы, играющие, роль переменных. Описать процедуру, которая:
а)* упрощает дерево-формулу T, заменяя в нем все поддеревья, соответствующие формулам (f+0), (0+f),(f—0),
(f*1) и (1*f), на поддеревья, соответствующие формуле f, а поддеревья, соответствующие формулам (f*0) и (0*f),—. на вершину с 0;
б) преобразует дерево-формулу Т, заменяя в нем все поддеревья, соответствующие формулам (f1± f2)*f3) и (f1*(f2±f3), на поддеревья, cоответствующие формулам:
((f1* f3) ± (f2* f3)) ((f1* f2) ± (f1* f3))
в) выполняет в дереве-формуле Т преобразования, обратные преобразованиям из п. б;
г) cтроит дерево-формулу Т1 —производную дерева- формулы Т' по переменной, однобуквенное имя которой являет значением литерного параметра v.
17.15. Предложить и описать на Паскале представление в виде двоичного дерева для формул из упр. 17.13, в которых в качестве терминалов используются любые неотрицательные целые числа. Для такого представления реализовать те же операции, что и в упр. 17.13.
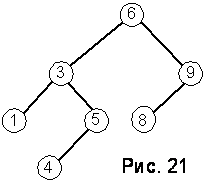
17.16. Деревом поиска, или таблицей в виде дерева, называется двоичное дерево в котором слева от любой вершины находятся вершины с элементами, меньшими элемента из этой вершины, а справа— с большими элементами (предполагается, что все элементы дерева попарно различны и что их тип (ТЭД) допускает применение операций сравнения); пример такого дерева показан на рис. 21.
Считая описанными тип дерево (см. выше) и тип файл
type файл=file of ТЭД;
определить функцию или процедуру, которая:
а) проверяет, входит ли элемент Е в дерево поиска Т;
б) записывает в файл f элементы дерева поиска Т в порядке их возрастания;
в) добавляет к дереву поиска Т новый элемент Е, если его не было в T;
г) по файлу f, все элементы которого различны, строит соответствующее дерево поиска Т.
17.17. Во внешнем текстовом файле PROG записана (без ошибок) некоторая программа на языке Паскаль. Известно, что в этой программе каждый идентификатор (служебное слово или имя) содержит не более 9 латинских букв и или цифр. Напечатать в алфавитном порядке все различные идентификаторы этой программы, указав для каждого из них число его вхождении в текст программы. (Учесть, что в идентификаторах одноименные прописные и строчные буквы отождествляются, что внутри литерных 
значений, строк-констант и комментариев последовательности из букв и цифр не являются идентификаторами, и что в записи вещественных чисел может встретиться буква Е или е.)
Для хранения идентификаторов использовать дерево поиска, элементами которого являются пары—идентификаторы и число его вхождений в текст программы.
17.18. Решить предыдущую задачу, но вместе с каждым идентификатором печатать в возрастающем порядке номера всех строк текста программы, в которых он встречается.
17.19. Решить задачу 17.17 при условии, что максимальная длина идентификаторов заранее не известна.
17.20. Решить задачу 17.18 при условии, что максимальная длина идентификаторов заранее не известна.