Лемма [1]. Пусть  – наследственная формация. Тогда следующие утверждения эквивалентны:
– наследственная формация. Тогда следующие утверждения эквивалентны:
1)  обладает решеточным свойством для
обладает решеточным свойством для  -субнормальных подгрупп;
-субнормальных подгрупп;
2) группа  принадлежит
принадлежит  , если
, если  ,
,  –
–  -субнормальные
-субнормальные  -подгруппы группы
-подгруппы группы  ;
;
3)  – формация Фиттинга и всякая
– формация Фиттинга и всякая  -субнормальная
-субнормальная  -подгруппа группы
-подгруппа группы  содержится в
содержится в  -радикале этой группы.
-радикале этой группы.
Установим, что из 1) следует 2).
Пусть  – контрпример минимального порядка. В этом случае
– контрпример минимального порядка. В этом случае 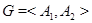 , где
, где 
 -субнормальная
-субнормальная  -подгруппа группы
-подгруппа группы  ,
, 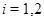 , и
, и  не принадлежит
не принадлежит  . Пусть
. Пусть 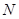 – минимальная нормальная подгруппа группы
– минимальная нормальная подгруппа группы  . Все условия леммы для фактор-групп выполняются, поэтому в силу выбора
. Все условия леммы для фактор-групп выполняются, поэтому в силу выбора  имеем, что
имеем, что  . В виду теоремы 4.3 из [7] формация
. В виду теоремы 4.3 из [7] формация  является насыщенной. Поэтому группа
является насыщенной. Поэтому группа  имеет единственную минимальную нормальную подгруппу
имеет единственную минимальную нормальную подгруппу  и
и  .
.
Если  , то
, то  – простая группа. Так как
– простая группа. Так как  и
и  –
–  -субнормальная подгруппа группы
-субнормальная подгруппа группы  ,
,  , то либо
, то либо  , либо
, либо  . Значит,
. Значит,  . Противоречие с выбором группы
. Противоречие с выбором группы  .
.
Пусть  . Рассмотрим подгруппы
. Рассмотрим подгруппы  и
и  . Так как
. Так как  – собственная
– собственная  -субнормальная подгруппа
-субнормальная подгруппа  и
и  , то нетрудно видеть, что
, то нетрудно видеть, что 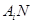 – собственная подгруппа
– собственная подгруппа  ,
,  . Покажем, что
. Покажем, что  .
.
Рассмотрим два случая.
1. Пусть 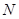 – абелева группа. Тогда
– абелева группа. Тогда 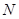 –
–  -группа,
-группа,  – простое число. Так как
– простое число. Так как  и подгруппа
и подгруппа 
 -субнормальна в
-субнормальна в  , то по лемме 2.6 получаем
, то по лемме 2.6 получаем  ,
,  .
.
2. Пусть 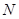 – неабелева группа. В этом случае
– неабелева группа. В этом случае

есть прямое произведение изоморфных неабелевых простых групп и  .
.
Рассмотрим подгруппу  . Так как подгруппа
. Так как подгруппа 
 -субнормальна в
-субнормальна в  , то ввиду леммы 2.4 и подгруппа
, то ввиду леммы 2.4 и подгруппа 
 -субнормальна в группе
-субнормальна в группе  . Пусть
. Пусть

Ввиду леммы 2.5 подгруппа 
 -субнормальна в
-субнормальна в  для любого
для любого  из
из  . Так как формация
. Так как формация  обладает решеточным свойством для
обладает решеточным свойством для 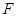 -субнормальных подгрупп, то
-субнормальных подгрупп, то  –
–  -субнормальная подгруппа
-субнормальная подгруппа  . Кроме того, из
. Кроме того, из  следует, что
следует, что  . Если
. Если  , то
, то  . Получили противоречие с
. Получили противоречие с  . Значит,
. Значит,  . Так как
. Так как  нормальна в
нормальна в  , то
, то  нормальна в
нормальна в  . Но
. Но
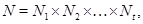
где  – неабелева простая группа и
– неабелева простая группа и  для всех
для всех  . Поэтому
. Поэтому

Из  и наследственности формации
и наследственности формации  следует, что
следует, что  . Но тогда
. Но тогда  . Далее, так как
. Далее, так как  , то по лемме 2.5 подгруппа
, то по лемме 2.5 подгруппа 
 -субнормальна в
-субнормальна в  . Значит, она
. Значит, она  -субнормальна и в
-субнормальна и в  ,
, 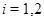 . Тогда из
. Тогда из  получаем что
получаем что

Пусть  – добавление к подгруппе
– добавление к подгруппе 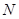 в группе
в группе  . Так как
. Так как  , то
, то  . В силу насыщенности формации
. В силу насыщенности формации  из
из

и

получаем, что 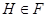 . Итак,
. Итак,  ,
, 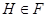 и
и  .
.
Используя тождество Дедекинда, имеем

Если предположить, что  , то
, то  . В этом случае
. В этом случае

Так как  , то
, то  не может быть
не может быть  -субнормальной подгруппой в
-субнормальной подгруппой в  . Следовательно, можно считать, что
. Следовательно, можно считать, что  ,
,  .
.
Так как подгруппа 
 -субнормальна в группе
-субнормальна в группе  и
и  , то из наследственности формации
, то из наследственности формации  следует, что подгруппа
следует, что подгруппа 
 -субнормальна в
-субнормальна в  .
.
Так как формация  обладает решеточным свойством для
обладает решеточным свойством для 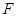 -субнормальных подгрупп, то
-субнормальных подгрупп, то 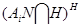 –
–  -субнормальная подгруппа группы
-субнормальная подгруппа группы  . Кроме того, из
. Кроме того, из 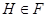 и наследственности формации
и наследственности формации  имеем
имеем  . Обозначим
. Обозначим  ,
, 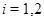 , и рассмотрим подгруппу
, и рассмотрим подгруппу  . Если
. Если  , то
, то  , что невозможно ввиду
, что невозможно ввиду  -субнормальности в
-субнормальности в  подгруппы
подгруппы  .
.
Пусть  . Из
. Из  , нормальности
, нормальности 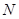 в
в  и нормальности
и нормальности  в
в  следует, что
следует, что  нормальна в
нормальна в  .
.
Так как

то

Таким образом получаем

Так как  , то
, то  – подгруппа из
– подгруппа из  . Тогда из
. Тогда из  -субнормальности в
-субнормальности в  подгрупп
подгрупп 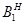 и
и  следует, что подгруппа
следует, что подгруппа

 -субнормальна в
-субнормальна в  . Это невозможно ввиду равенства
. Это невозможно ввиду равенства  . Значит,
. Значит,  . Противоречие.
. Противоречие.
Докажем, что из 2) следует 3). Пусть  , где
, где  – нормальная
– нормальная  -подгруппа группы
-подгруппа группы  ,
,  . Так как
. Так как

и  , то
, то  . Из наследственности формации
. Из наследственности формации  получаем, что подгруппа
получаем, что подгруппа 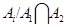
 -субнормальна в
-субнормальна в  . Ввиду леммы 2.6 подгруппа
. Ввиду леммы 2.6 подгруппа  теперь
теперь  -субнормальна в
-субнормальна в  ,
,  . Так как выполняется условие 2) леммы, то
. Так как выполняется условие 2) леммы, то

Следовательно,  – формация Фиттинга.
– формация Фиттинга.
Пусть  –
–  -субнормальная
-субнормальная  -подгруппа группы
-подгруппа группы  . Ввиду леммы 2.5 подгруппа
. Ввиду леммы 2.5 подгруппа 
 -субнормальна в
-субнормальна в 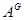 для всех
для всех  . Так как выполняются условия 2) леммы, то
. Так как выполняются условия 2) леммы, то

Отсюда следует, что

Наконец установим, что из 3) следует 1). Доказательство проведем индукцией по порядку группы  . Пусть
. Пусть 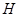 и
и  –
–  -субнормальные подгруппы группы
-субнормальные подгруппы группы  и
и  . Если
. Если 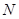 – минимальная нормальная подгруппа группы
– минимальная нормальная подгруппа группы  , то можно считать, что
, то можно считать, что  . Учитывая лемму 2.6 по индукции получаем, что
. Учитывая лемму 2.6 по индукции получаем, что  –
– 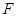 -субнормальная подгруппа группы
-субнормальная подгруппа группы  . На основании леммы 2.6 тогда подгруппа
. На основании леммы 2.6 тогда подгруппа 
 -субнормальна в
-субнормальна в  . Если
. Если  , то по индукции подгруппа
, то по индукции подгруппа 
 -субнормальна в
-субнормальна в  , и значит, ввиду леммы 2.5 она
, и значит, ввиду леммы 2.5 она  -субнормальна.
-субнормальна.
Будем далее считать, что  для любой минимальной нормальной подгруппы группы
для любой минимальной нормальной подгруппы группы  . Ясно, что
. Ясно, что  . Если
. Если  , то в силу леммы 3.1.3
, то в силу леммы 3.1.3  субнормальна в
субнормальна в  . Но тогда ввиду [8]
. Но тогда ввиду [8]

Это означает, что  . Противоречие. Значит
. Противоречие. Значит 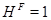 и
и 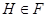 . Аналогично доказывается, что
. Аналогично доказывается, что  . Итак,
. Итак, 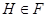 и
и  .
.
По условию леммы  – формация Фиттинга и
– формация Фиттинга и  ,
,  . Следовательно,
. Следовательно,

Пусть  – минимальная нормальная подгруппа группы
– минимальная нормальная подгруппа группы  , содержащейся в
, содержащейся в  . Тогда
. Тогда

Из наследственности формации  следует, что
следует, что  –
–  -субнормальная подгруппа группы
-субнормальная подгруппа группы  .
.
Итак, порождение двух  -субнормальных подгрупп
-субнормальных подгрупп  и
и  группы
группы 
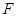 -субнормальна в
-субнормальна в  . Ввиду леммы 2.5
. Ввиду леммы 2.5  – также
– также  -субнормальная подгруппа группы
-субнормальная подгруппа группы  . Значит, формация
. Значит, формация  обладает решеточным свойством для
обладает решеточным свойством для  -субнормальных подгрупп. Лемма доказана.
-субнормальных подгрупп. Лемма доказана.
Лемма [1]. Пусть  – наследственная локальная формация. Если
– наследственная локальная формация. Если 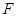 замкнута относительно расширений, то формация
замкнута относительно расширений, то формация  обладает решеточным свойством для
обладает решеточным свойством для  -субнормальных подгрупп.
-субнормальных подгрупп.
Доказательство леммы следует из теоремы 5 работы [9] и теоремы 3.1.7.
Отметим, что из леммы 3.2 следует, что формации  и
и  обладают решеточным свойством для
обладают решеточным свойством для  -субнормальных подгрупп.
-субнормальных подгрупп.
Пусть  обозначают некоторое подмножество множества натуральных чисел. Пусть
обозначают некоторое подмножество множества натуральных чисел. Пусть  – некоторое семейство классов групп. Обозначим через
– некоторое семейство классов групп. Обозначим через  класс всех групп
класс всех групп  , представимых в виде
, представимых в виде

где  и
и  ,
,  .
.
Лемма [1]. Справедливы следующие утверждения:
1) пусть  – наследственная локальная формация, обладающая решеточным свойством для
– наследственная локальная формация, обладающая решеточным свойством для  -субнормальных подгрупп,
-субнормальных подгрупп,  . Тогда и формация
. Тогда и формация 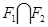 обладает решеточным свойством для
обладает решеточным свойством для  -субнормальных подгрупп;
-субнормальных подгрупп;
2) пусть  – некоторое семейство наследственных локальных формаций и
– некоторое семейство наследственных локальных формаций и  для любых
для любых  . Тогда и только тогда формация
. Тогда и только тогда формация

обладает решеточным свойством для  -субнормальных подгрупп, когда для каждого
-субнормальных подгрупп, когда для каждого 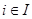 формация
формация  обладает решеточным свойством для
обладает решеточным свойством для  -субнормальных подгрупп.
-субнормальных подгрупп.
Пусть формация  обладает решеточным свойством для
обладает решеточным свойством для  -субнормальных подгрупп,
-субнормальных подгрупп,  . Ввиду леммы 3.1
. Ввиду леммы 3.1  и
и  – формации Фиттинга поэтому из леммы 2.1.3 следует, что
– формации Фиттинга поэтому из леммы 2.1.3 следует, что  также является формацией Фиттинга.
также является формацией Фиттинга.
Пусть  –
–  -субнормальная подгруппа группы
-субнормальная подгруппа группы  и
и  . Ясно, что подгруппа
. Ясно, что подгруппа 
 -субнормальна в
-субнормальна в  для любого
для любого  . Так как
. Так как  и
и  , то ввиду леммы 3.1 получаем, что
, то ввиду леммы 3.1 получаем, что 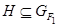 и
и 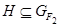 . Следовательно,
. Следовательно,

Теперь утверждение 1 следует из леммы 3.1.
Докажем утверждение 2). Пусть формация

обладает решеточным свойством для  -субнормальных подгрупп. Отметим, что
-субнормальных подгрупп. Отметим, что  . Отсюда ввиду утверждения 1) настоящей леммы и леммы 3.2 следует, что формация
. Отсюда ввиду утверждения 1) настоящей леммы и леммы 3.2 следует, что формация  обладает решеточным свойством для
обладает решеточным свойством для  - субнормальных подгрупп.
- субнормальных подгрупп.
Обратно, пусть для любого 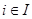 формация
формация  обладает решеточным свойством для
обладает решеточным свойством для  -субнормальных подгрупп. Пусть
-субнормальных подгрупп. Пусть

Индукцией по порядку группы  покажем, что любая группа
покажем, что любая группа  , где
, где  ,
,  –
–  -субнормальные
-субнормальные  -подгруппы группы
-подгруппы группы  принадлежат
принадлежат 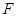 .
.
Пусть  – минимальная нормальная подгруппа группы
– минимальная нормальная подгруппа группы  . Ввиду леммы 2.6 из соображений индукции получаем, что
. Ввиду леммы 2.6 из соображений индукции получаем, что  . Так как
. Так как 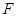 – насыщенная формация, то
– насыщенная формация, то  имеет единственную минимальную нормальную подгруппу
имеет единственную минимальную нормальную подгруппу  и
и  . Ясно, что
. Ясно, что

Отметим также, что
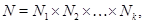
где  – изоморфные простые группы для
– изоморфные простые группы для  .
.
Докажем, что  . Рассмотрим группу
. Рассмотрим группу  . Так как подгруппа
. Так как подгруппа 
 -субнормальна в
-субнормальна в  , то
, то  . Тогда по индукции
. Тогда по индукции

Рассмотрим пересечение  . Если
. Если
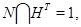
то

Отсюда и из того факта, что  – нормальная подгруппа
– нормальная подгруппа  и
и  следует, что
следует, что  .
.
Пусть  . Так как
. Так как  – нормальная подгруппа из
– нормальная подгруппа из  , то
, то  – нормальная подгруппа из
– нормальная подгруппа из 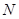 . А это значит, что
. А это значит, что

Из наследственности формации  и
и  получаем, что
получаем, что  . Но тогда
. Но тогда  .
.
Из строения  и
и

для любых  , следует, что
, следует, что  для некоторого
для некоторого  . Так как
. Так как

то нетрудно видеть, что группа  имеeт
имеeт  -холловскую подгруппу
-холловскую подгруппу  .
.
Так как  , то
, то  –
–  -субнормальная подгруппа группы
-субнормальная подгруппа группы  . Так как
. Так как  ,
,  и
и  ,
,  –
–  -субнормальные подгруппы, то по индукции имеем, что
-субнормальные подгруппы, то по индукции имеем, что

Отсюда и из  ввиду
ввиду  получаем
получаем  . Аналогично доказывается, что
. Аналогично доказывается, что  . Таким образом,
. Таким образом,

Отсюда и из  -субнормальности
-субнормальности  и
и  в
в  нетрудно заметить, что
нетрудно заметить, что  ,
,  –
–  -субнормальные подгруппы группы
-субнормальные подгруппы группы  . Из
. Из  и
и  ввиду наследственности
ввиду наследственности  следует, что
следует, что  и
и  . Так как по условию формация
. Так как по условию формация  обладает решеточным свойством для
обладает решеточным свойством для  - субнормальных подгрупп, то ввиду леммы 3.1
- субнормальных подгрупп, то ввиду леммы 3.1

Итак,  содержит некоторую группу
содержит некоторую группу  , где
, где  ,
,  –
–  -субнормальные
-субнормальные  -подгруппы группы
-подгруппы группы  . Следовательно, ввиду леммы 3.1 формация
. Следовательно, ввиду леммы 3.1 формация 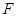 обладает решеточным свойством для
обладает решеточным свойством для  -субнормальных подгрупп. Лемма доказана.
-субнормальных подгрупп. Лемма доказана.
Лемма [1]. Пусть  – нормально наследственная разрешимая формация. Тогда справедливы следующие утверждения:
– нормально наследственная разрешимая формация. Тогда справедливы следующие утверждения:
1) если в каждой разрешимой группе все  -субнормальные подгруппы образуют решетку, то
-субнормальные подгруппы образуют решетку, то  имеет вид
имеет вид
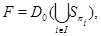
где  для любых
для любых  из
из 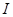 ;
;
2) если  – формация из пункта 1), то она обладает решеточным свойством для
– формация из пункта 1), то она обладает решеточным свойством для  -субнормальных подгрупп.
-субнормальных подгрупп.
1) Покажем, что  является либо группой Шмидта, либо группой простого порядка. Очевидно, что
является либо группой Шмидта, либо группой простого порядка. Очевидно, что  и
и  .
.
Пусть  – максимальный внутренний локальный экран формации
– максимальный внутренний локальный экран формации  . Согласно лемме 2.3
. Согласно лемме 2.3

где  – единственная минимальная нормальная подгруппа группы
– единственная минимальная нормальная подгруппа группы  ,
,  (
( – простое число), а
– простое число), а  – максимальная подгруппа группы
– максимальная подгруппа группы  , являющейся минимальной не
, являющейся минимальной не  -группой.
-группой.
Докажем, что  – циклическая
– циклическая  -группа для некоторого простого числа
-группа для некоторого простого числа  . Допустим противное. Тогда в
. Допустим противное. Тогда в  найдутся по крайней мере две несопряженные максимальные подгруппы
найдутся по крайней мере две несопряженные максимальные подгруппы  и
и  . Рассмотрим в
. Рассмотрим в  подгруппу
подгруппу  ,
,  . Ясно, что
. Ясно, что 
 -субнормальна в
-субнормальна в  ,
,  . Из
. Из  ,
,  и
и  по лемме 3.1 получаем, что
по лемме 3.1 получаем, что  . Получили противоречие с выбором
. Получили противоречие с выбором  .
.
Следовательно,  – циклическая группа порядка
– циклическая группа порядка  , где
, где  – некоторое простое число,
– некоторое простое число,  ,
,  – натуральное число. Допустим, что
– натуральное число. Допустим, что  . Обозначим через
. Обозначим через  – регулярное сплетение циклических групп
– регулярное сплетение циклических групп  и
и  соответственно порядков
соответственно порядков  и
и  .
.
По теореме 6.2.8 из [2]  изоморфна некоторой подгруппе группы
изоморфна некоторой подгруппе группы  . Так как
. Так как  и
и  , то ввиду теоремы 2.4 из [5]
, то ввиду теоремы 2.4 из [5] 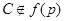 .
.
Рассмотрим регулярное сплетение 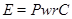 , где
, где  . Тогда
. Тогда  , где
, где  – элементарная абелева
– элементарная абелева  -группа. Так как
-группа. Так как  , то
, то  . Из
. Из

следует что  .
.
Рассмотрим в  подгруппы
подгруппы  и
и 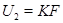 , где
, где  – база сплетения
– база сплетения  . Ясно, что
. Ясно, что 
 -субнормальна в
-субнормальна в  ,
, 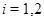 . Кроме того,
. Кроме того,  . Отсюда
. Отсюда

Так как  , то
, то  по лемме 3.1. Получили противоречие.
по лемме 3.1. Получили противоречие.
Следовательно,  и
и  – группа Шмидта. Если
– группа Шмидта. Если  и
и  , то по лемме 1.1.6
, то по лемме 1.1.6  также является группой Шмидта. Таким образом, любая разрешимая минимальная не
также является группой Шмидта. Таким образом, любая разрешимая минимальная не  -группа является либо группой Шмидта, либо имеет простой порядок. Тогда по лемме 3.1.12
-группа является либо группой Шмидта, либо имеет простой порядок. Тогда по лемме 3.1.12  является наследственной формацией.
является наследственной формацией.
Покажем, что формация  имеет такой локальный экран
имеет такой локальный экран  , что
, что

p(F)  p'(F)
p'(F)  p(F)
p(F)  Действительно. Пусть
Действительно. Пусть 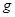 – локальный экран формации
– локальный экран формации  . Так как
. Так как 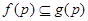 для любого простого числа
для любого простого числа  из
из  , то
, то  . Покажем обратное.
. Покажем обратное.
Пусть  – группа минимального порядка из
– группа минимального порядка из  . Так как
. Так как  – наследственная формация и
– наследственная формация и  – насыщенная формация, то
– насыщенная формация, то  – минимальная не
– минимальная не  -группа и
-группа и  . Теперь, согласно лемме 2.3
. Теперь, согласно лемме 2.3

где  – единственная минимальн
– единственная минимальн