Определение производной
Пусть функция y = f(x) определена в промежутке X. Производной функции y = f(x) в точке хo называется предел
 =
= 
Если этот предел конечный, то функция f(x) называется дифференцируемой в точке xo; при этом она оказывается обязательно и непрерывной в этой точке.Если же рассматриваемый предел равен ∞ (или -∞), то при условии, что функция в точке хo непрерывна, будем говорить, что функция f(x) имеет в точке хo бесконечную производную. Производная обозначается символами
y ', f ' (xo),  ,
,  .
.
Нахождение производной называется дифференцированием функции. Геометрический смысл производной состоит в том, что производная есть угловой коэффициент касательной к кривой y=f(x) в данной точке хo; физический смысл - в том, что производная от пути по времени есть мгновенная скорость движущейся точки при прямолинейном движении s = s(t) в момент t0.
Правила дифференцирования
Если с - постоянное число, и u = u(x), v = v(x) - некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
1) (с) ' = 0, (cu) ' = cu';
2) (u+v)' = u'+v';
3) (uv)' = u'v+v'u;
4) (u/v)' = (u'v-v'u)/v2;
5) если y = f(u),
u = j(x), т.е. y = f(j(x)) - сложная функция, или суперпозиция, составленная из дифференцируемых функций j и f, то  , или
, или  ;
;
6) если для функции y = f(x) существует обратная дифференцируемая функция x = g(y), причем  ≠ 0, то
≠ 0, то  .
.
Таблица производных
На основе определения производной и правил дифференцирования можно составить список табличных производных основных элементарных функций.
1. (um)' = m um-1 u' (m принадлежит R1 )
2. (au)' = au lna× u'.
3. (eu)' = eu u'.
4. (loga u)' = u'/(u ln a).
5. (ln u)' = u'/u.
6. (sin u)' = cos u× u'.
7. (cos u)' = - sin u× u'.
8. (tg u)' = 1/ cos2u× u'.
9.(ctg u)' = - u' / sin2u.
10. (arcsin u)' = u' / 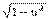 .
.
11. (arccos u)' = - u' / 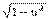 .
.
|
|
12. (arctg u)' = u'/(1 + u2).
13. (arcctg u)' = - u'/(1 + u2).
Вычислим производную степенно-показательного выражения y = uv, (u>0), где u и v суть функции от х, имеющие в данной точке производные u', v'. Прологарифмировав равенство y=u v, получим ln y = v ln u. Приравнивая производные по х от обеих частей полученного равенства с помощью правил 3, 5 и формулы для производной логарифмической функции, будем иметь:y'/y = vu'/u +v' ln u, откуда y' = y (vu'/u +v' ln u). Итак, (u v)'=u v (vu'/u+v' ln u), u > 0. Например, если y = x sin x, то y' = x sin x (sin x/x + cos x× ln x). Если функция y = f(x) дифференцируема в точке x, т.е. имеет в этой точке конечную производную y', то  = y'+ α, где α→0 при Δх →0; отсюда Δy = y' Δх + αx. Главная часть приращения функции, линейная относительно Δх, называется дифференциалом функции и обозначается dy: dy = y' Δх. Если положить в этой формуле y = x, то получим dx = x'Δх = 1×Δх =Δх, поэтому dy=y'dx, т. е. символ для обозначения производной
= y'+ α, где α→0 при Δх →0; отсюда Δy = y' Δх + αx. Главная часть приращения функции, линейная относительно Δх, называется дифференциалом функции и обозначается dy: dy = y' Δх. Если положить в этой формуле y = x, то получим dx = x'Δх = 1×Δх =Δх, поэтому dy=y'dx, т. е. символ для обозначения производной  можно рассматривать как дробь. Приращение функции Δy есть приращение ординаты кривой, а дифференциал d y есть приращение ординаты касательной.
можно рассматривать как дробь. Приращение функции Δy есть приращение ординаты кривой, а дифференциал d y есть приращение ординаты касательной.

Производные высшего порядка
Пусть мы нашли для функции y = f(x) ее производную y '= f '(x). Производная от этой производной называется производной второго порядка функции f(x), или второй производной, и обозначается  . Аналогично определяются и обозначаются: производная третьего порядка -
. Аналогично определяются и обозначаются: производная третьего порядка -  , производная четвертого порядка -
, производная четвертого порядка - 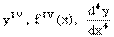 и вообще производная n-го порядка -
и вообще производная n-го порядка - 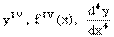 .
.
Пример 3. 15. Вычислить производную функции y=(3x3-2x+1)×sin x.
Решение. По правилу 3, y'=(3x3-2x+1)'×sin x + (3x3-2x+1)×(sin x)' = = (9x2-2)sin x + (3x3-2x+1)cos x.