Классификация средств измерения

По метрологическому назначению средства измерений подразделяются на:

- рабочие средства измерений, предназначенные для измерений физических величин, не связанных с передачей размера единицы другим средствам измерений. (Пример РСИ электросчетчик для измерения электрической энергии);

- образцовые средства измерений, предназначенные для обеспечения единства измерений в стране.

По степени автоматизации средства измерений подразделяются на:

- автоматические, производящие в автоматическом режиме все операции, связанные с обработкой результатов измерений, их регистрацией, передачей данных или выработкой управляющего сигнала;

- автоматизированные, производящие в автоматическом режиме одну или часть измерительных операций;

- неавтоматические, не имеющие устройств для автоматического выполнения измерений и обработки их результатов (рулетка, теодолит- для измерения плоских углов).

По стандартизации средства измерений подразделяются на:

- стандартизованные, изготовленные в соответствии с требованиями государственного или отраслевого стандарта;

- не стандартизованные - уникальные средства измерений, предназначенные для специальной измерительной задачи, в стандартизации требований к которому нет необходимости. Не стандартизованные средства измерений не подвергаются государственным испытаниям (поверкам), а подлежат метрологическим аттестациям.

По конструктивному исполнению средства измерений подразделяются на:

- меры;

- измерительные преобразователи;

- измерительные приборы;

- измерительные установки;

Погрешность измерения — оценка отклонения величины измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения.

Абсолютная погрешность — Δ X является оценкой абсолютной ошибки измерения. Величина этой погрешности зависит от способа её вычисления, который, в свою очередь, определяется распределением случайной величины Xmeas. При этом неравенство:

Δ X | Xtrue − Xmeas |,

где Xtrue — истинное значение, а Xmeas — измеренное значение, должно выполняться с некоторой вероятностью близкой к 1. Если случайная величина Xmeas распределена по нормальному закону, то, обычно, за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина.

Относительная погрешность — отношение абсолютной погрешности к тому значению, которое принимается за истинное:

.

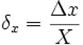Относительная погрешность является безразмерной величиной, либо измеряется в процентах.

Приведённая погрешность — погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле

,

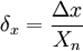где Xn — нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:

— если шкала прибора односторонняя, то есть нижний предел измерений равен нулю, то Xn определяется равным верхнему пределу измерений;

— если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.

Приведённая погрешность является безразмерной величиной, либо измеряется в процентах).

Термин "поверка" введен ГОСТ "ГСИ. Метрология. Термины и определения." как "определение метрологическим органом погрешностей средств измерений и установление его пригодности к применению". Поверке подвергаются средства измерений, выпускаемые из производства и ремонта, получаемые из-за рубежа, а также находящиеся в эксплуатации и хранении.

При поверке измерительного прибора (ИП) определяют погрешности его показаний и сравнивают их с данными, указанными в технических требованиях Обозначим:

Δφ - действительные погрешности показаний,

Δφпр - пределы допускаемых погрешностей, установленные стандарта­ми и другими нормами.

Если Δφ < Δφпр, то ИП признают годным. Однако, при поверке возникают свои погрешности. В результате нарушается достоверность поверки. Например, поверяемый прибор, в действительности годный, бракуют из-за погрешности поверки. Этот случай называют ошибкой 1-го рода (или Г-Б, т,е. перевод годных в бракованные). Возможно и обратное явление: поверяемый прибор в действительности не годен, но его можно принять как годный также вследствие погрешности поверки. Второй случай называют ошибкой 2-го рода (или Б-Г, т.е. перевод бракованных в годные).

Указанные явление должны быть сведены к минимуму. Для этого сначала исключают систематические погрешности поверки. Остаются случайные по­грешности поверки. Их исключить нельзя, можно только учесть.

Погрешность поверки есть разность между погрешностью показаний ИП, найденной экспериментально, и истинным значением погрешности показаний Δ₀φ. Но Δ₀φ всегда остается неизвестным, поэтому вместо него принимают требуемое точное значение погрешности, для которого устанавливают свой доверительный интервал (значительно более узкий, чем для погрешности пока­заний поверяемого ИП). На практике это требуемое точное значение погреш­ности показаний находят как оценку среднего значения погрешности показа­ний при многократной поверке Δ2φ.

Градуировкой называется процесс нанесения отметок на шкалы средств измерений, а также определение значений измеряемой величины, соответствующих уже нанесенным отметкам для составления градуировочных кривых или таблиц.

Различают следующие способы градуировки.

1. Использование типовых шкал. Для подавляющего большинства рабочих и многих образцовых приборов используют типовые шкалы, которые изготовляются заранее в соответствии с уравнением статической характеристики идеального прибора. При регулировке параметрам элементов прибора экспериментально придают такие значения, при которых погрешность в точках регулировки становится равной нулю.

2. Индивидуальная градуировка шкал. Индивидуальную градуировку шкал осуществляют в тех случаях, когда статическая характеристика прибора нелинейная или близка к линейной, но характер изменения систематической погрешности в диапазоне измерения случайным образом меняется от прибора к прибору данного типа так, что регулировка не позволяет уменьшить основную погрешность до пределов ее допускаемых значений.

3. Градуировка условной шкалы. Условной называется шкала, снабженная некоторыми условными равномерно нанесенными делениями, например через миллиметр или угловой градус. В результате определяют зависимость числа делений шкалы, пройденных указателем от значений измеряемой величины. Эту зависимость представляют в виде таблицы или графика