Момент силы как функция от времени

Билет 1

Поступательное движение — это механическое движение системы точек (тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени.

Траектория материальной точки — линия в трёхмерном пространстве, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве

пройденный путь - это длина траектории.

Перемещением материальной точки (тела) называется вектор, проведённый из начального положения материальной точки в конечное.

Очевидно, что модуль вектора перемещения - это кратчайшее расстояние между начальным и конечным положениями материальной точки. Перемещение характеризует изменение положения тела интегрально (суммарно). Оно не показывает каким образом происходил этот процесс

Скорость (часто обозначается , от англ. velocity или фр. vitesse) — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта (например угловая скорость). Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.

Ускорение (обычно обозначается , в теоретической механике ), производная скорости по времени — векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её движении за единицу времени (т.е. ускорение учитывает не только изменение величины скорости, но и её направления

Тангенциальное ускорение — компонент ускорения, направленный по касательной к траектории движения. Совпадает с направлением вектора скорости при ускоренном движении и противоположно направлено при замедленном. Характеризует изменение модуля скорости

Билет 2

Угловая скорость — векторная величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.

Угловое ускорение — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.

При вращении тела вокруг неподвижной оси, угловое ускорение по модулю равно^[1]:

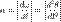Вектор углового ускорения α направлен вдоль оси вращения (в сторону при ускоренном вращении и противоположно — при замедленном).

При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости ω по времени^[2], то есть

Связь между линейными и угловыми величинами, характеризующими вращение материальной точки, выражается следующими формулами:

путь, пройденный точкой по дуге окружности радиусом R,

s= R ( — угол поворота тела);скорость точки линейная ускорение точки: тангенциальное нормальное

Билет 3

Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между равнодействующей всех приложенных к телу сил и ускорением этого тела. Один из трёх Ньютона. Второй закон Ньютона утверждает: в инерциальных системах ускорение, приобретаемое материальной точкой (телом), прямо пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела).Этот закон записывается в виде формулы: ,где — ускорение тела, — сила, приложенная к телу, а — масса тела, причём — константа. Или, в более известном виде: в тех же обозначениях. В случае, если масса тела меняется со временем, то второй закон Ньютона записывается в общем виде (в таком виде его написал сам Ньютон): где — импульс (количество движения) тела, — время, а — производная по времени. Второй закон Ньютона справедлив только для скоростей, много меньших скорости света и в инерциальных системах отсчёта. Закон сохранения импульса (Закон сохранения количества движения) утверждает, что сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил. В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона.

Билет 4

Если действующая на тело сила F вызывает его перемещение s, то действие этой силы характеризуется величиной, называемой механической работой (или, сокращенно, просто работой). Механической работой А называют скалярную величину, равную произведению модуля силы F, действующей на тело, и модуля перемещения s, совершаемого телом в направлении действия этой силы, т. е. А=Fs. Таким образом, в общем случае механическая работа равна произведению модуля силы и модуля перемещения на косинус угла между направлениями силы и перемещения. Работа силы, направленной вдоль перемещения тела, положительна, а силы, направленной против перемещения тела, - отрицательна. По формулам (3.9) и (3.10) вычисляют работу постоянной силы. Единицу механической работы устанавливают из формулы (3.9). В СИ за единицу работы принята работа силы 1 Н при перемещении точки ее приложения на 1 м. Эта единица имеет наименование джоуль (Дж): 1 Дж = 1Н·1м.

Мощностью N называют величину, равную отношению работы А к промежутку времени t, в течение которого эта работа была совершена:N=A/tИз формулы следует, что в СИ единицей мощности яв-ляется 1 Дж/с (джоуль в секунду). Эту единицу иначе называют ватт (Вт), 1 Вт= 1 Дж/с.Связь между мощностью и скоростью при равномерном движении найдем, подставив (3.10) в (3.11):N=Fvcosa.(Эта формула справедлива и для переменного движения, если под N понимать мгновенную мощность, а под V - мгновенную скорость). Если направление силы совпадает с направлением перемещения, то cosa=1 и N=Fv. Из последней формулы следует, что F=N/v и v=N/F.Из этих формул видно, что при постоянной мощности двигателя скорость движения обратно пропорциональна силе тяги и наоборот. На этом основан принцип действия коробки скоростей (коробки перемены передач) различных транспортных средств Физический смысл кинетической энергии:кинетическая энергия тела, движущегося со скоростью υ, показывает, какую работу должна совершить сила, действующая на покоящееся тело, чтобы сообщить ему эту скорость Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела. Кинетическая энергия обозначается буквой E_k. Тогда равенство (1) можно записать в таком виде: A = E_k2 – E_k1. (3) Теорема о кинетической энергии:

работа равнодействующей сил, приложенных к телу, равна изменению кинетической энергии тела.

Так как изменение кинетической энергии равно работе силы (3), кинетическая энергия тела выражается в тех же единицах, что и работа, т. е. в джоулях.

Если начальная скорость движения тела массой т равна нулю и тело увеличивает свою скорость до значения υ, то работа силы равна конечному значению кинетической энергии тела: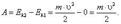

Потенциальная энергия тела - это его запасенная энергия. Если тело поднять над землей - у него появится запас энергии.
Если его отпустить, запас начнет расходоваться и переходить в кинетическую энергию. Её ещё называют энергией движения

Потенциальная энергия — скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет его нахождения в поле действия сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы^[1]. Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином.

Единицей измерения энергии в СИ является Джоуль.

Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения.

Билет 5

Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что энергия изолированной (замкнутой) физической системы сохраняется с течением времени. Другими словами, энергия не может возникнуть из ничего и не может исчезнуть в никуда, она может только переходить из одной формы в другую Закон сохранения механической энергии может быть выведен из второго закона Ньютона^[5], если учесть, что в консервативной системе все силы, действующие на тело, потенциальны и, следовательно, могут быть представлены в виде ,где — потенциальная энергия материальной точки (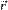 — радиус-вектор точки пространства). В этом случае второй закон Ньютона для одной частицы имеет вид ,где m — масса частицы, — вектор её скорости. 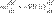Скалярно домножив обе части данного уравнения на скорость частицы и приняв во внимание, что , можно получить Путём элементарных операций это выражение может быть приведено к следующему виду Отсюда непосредственно следует, что выражение, стоящее под знаком дифференцирования по времени, сохраняется. Это выражение и называется механической энергией материальной точки. Первый член в сумме отвечает кинетической энергии, второй — потенциальной.Этот вывод может быть легко обобщён на систему материальных точек^[В термодинамике исторически закон сохранения формулируется в виде первого принципа термодинамики:Изменение внутренней энергии термодинамической системы при переходе её из одного состояния в другое равно сумме работы внешних сил над системой и количества теплоты, переданного системе, и не зависит от способа, которым осуществляется этот переход

или альтернативно^[6]:Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних силВ математической формулировке это может быть выражено следующим образом: ,

где введены обозначения Q — количество теплоты, полученное системой, Δ U — изменение внутренней энергии системы, A — работа, совершённая системой.Закон сохранения энергии, в частности, утверждает, что не существует вечных двигателей первого рода, то есть невозможны такие процессы, единственным результатом которых было бы производство работы без каких-либо изменений в других телах.

Билет 6

Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).Единица измерения СИ: кг·м².Обозначение: I или J. Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется физическая величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси: 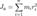,где: m_i — масса i -й точки, r_i — расстояние от i -й точки до оси.Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении. ,где: dm = ρ dV — масса малого элемента объёма тела dV,ρ — плотность, r — расстояние от элемента dV до оси a.Если тело однородно, то есть его плотность всюду одинакова, то Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

Если — момент инерции тела относительно оси, проходящей через центр масс тела, то момент инерции относительно параллельной оси, расположенной на расстоянии от неё, равен ,где — полная масса тела.Например, момент инерции стержня относительно оси, проходящей через его конец, равен:

Найдем момент инерции однородного сплошного цилиндра высотой h, радиусом R относительно его геометрической оси. Разобьем цилиндр на бесконечно малые, толщины d r, полые концентрические цилиндры с внутренним радиусом r и внешним радиусом r + d r. В момент инерции каждого полого цилиндра определяется:Т.к. d r << r, то расстояние от оси до точек цилиндра равно r. d m — масса всего элементарного цилиндра, его объем d V = 2p r h d r. Если r — это плотность материала, то m = r× V, тогда d m = 2p× r × h ×r×d r. Отсюда d I = 2p× h ×r× r ³×d r, тогда Нахождение момента инерции для цилиндра упрощалось вследствие того, что тело было однородным и симметричным, а момент инерции искали относительно оси симметрии. Момент инерции относительно любой другой оси можно определить с помощью теоремы Штейнера, или еще говорят — Гюггенса-Штейнера.ТЕОРЕМА: Момент инерции тела относительно произвольной оси равен моменту инерции его относительно параллельной оси, проходящей через центр масс тела, сложенному с произведением массы тела на квадрат расстояния между осями. I = I_c + ma ² (3)

Билет 7

Кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек па которые это тело можно разбить:

Если тело вращается вокруг неподвижной оси с угловой скоростью , то линейная скорость i-ой точки равна , где , - расстояние от этой точки до оси вращения. Следовательно.

где - момент инерции тела относительно оси вращения. В общем случае движение твердого тела можно представить в виде суммы двух движений - поступательного со скоростью, равной скорости центра инерции тела, и вращения с угловой скоростью вокруг мгновенной оси, проходящей через центр инерции. При этом выражение для кинетической энергии тела преобразуется к виду

где - момент инерции тела относительно мгновенной оси вращения, проходящей через центр инерции.

Билет 8

Момент силы (синонимы: крутящий момент; вращательный момент; вертящий момент; вращающий момент) — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси вращения рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метров от его оси вращения, это то же самое, что сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров до оси вращения. Более точно, момент силы частицы определяется как векторное произведение: где — сила, действующая на частицу, а — радиус-вектор частицы.

Момент силы как функция от времени

Момент силы — производная по времени от момента импульса, ,где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости. ,То есть если I постоянная, то 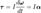,где α — угловое ускорение, измеряемое в радианах в секунду за секунду.

Момент импульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — скалярная величина

Определение Момент импульса частицы относительно некоторого начала отсчёта определяется векторным произведением ее радиус-вектора и импульса:

где — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчета начала отсчёта, — импульс частицы. В системе СИ момент импульса измеряется в единицах джоуль - секунда; Дж·с.Из определения момента импульса следует его аддитивность. Так, для системы частиц выполняется выражение: Закон сохранения момента импульса (закон сохранения углового момента) — векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной в случае равновесия системы. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем.

Билет 9

Вращением вокруг неподвижной оси называется такое движение твердого тела, при котором во все время движения две его точки остаются неподвижными. Прямая, проходящая через эти точки, называется осью вращения. Все остальные точки тела движутся в плоскостях, перпендикулярных оси вращения, по окружностям, центры которых лежат на оси вращения. Положение вращающегося твердого тела определяется одним параметром - углом φ между начальным положением АМ₀О некоторой плоскости, связанной с телом и проходящей через ось, и ее положением АМ₀ О в данный момент времени Закон вращательного движения:

Проекция вектора угловой скорости на ось и определяется зависимостью:

Угловая скорость ω рад/сек связана с числом оборотов в минуту n зависимостями:

Проекция вектора угловой скорости на ось u определяется зависимостью Скорость и ускорение точки М вращающегося твердого тела определяются соотношениями (рис. 1): или в скалярной форме: Частные случаи:1) равномерное вращение (ε=0) 2) равнопеременное вращение (ε_u=const):

Билет 10

В рамках классической механики гравитационное взаимодействие описывается законом всемирного тяготения. Этот закон был открыт Ньютоном в 1666 г.. Он гласит, что сила гравитационного притяжения между двумя материальными точками массы m ₁ и m ₂, разделёнными расстоянием R, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними — то есть Здесь G — гравитационная постоянная, равная м³/(кг с²). В ньютоновской теории каждое массивное тело порождает силовое поле притяжения к этому телу, которое называется гравитационным полем. Это поле потенциально, и функция гравитационного потенциала для материальной точки с массой M определяется формулой: В общем случае, когда плотность вещества ρ распределена произвольно, φ удовлетворяет уравнению Пуассона: Решение этого уравнения записывается в виде: где r — расстояние между элементом объёма dV и точкой, в которой определяется потенциал φ, С — произвольная постоянная.Сила притяжения, действующая в гравитационном поле на материальную точку с массой m, связана с потенциалом формулой: .Сферически симметричное тело создаёт такое же притяжение, как материальная точка той же массы, расположенная в центре тела.Траектория материальной точки в гравитационном поле, создаваемом много большей по массе материальной точкой, подчиняется законам Кеплера. В частности, планеты и кометы в Солнечной системе движутся по эллипсам или гиперболам. Влияние других планет, искажающее эту картину, можно учесть с помощью теории возмущений.

Вес — сила воздействия тела на опору (или другой вид крепления в случае подвешенных тел), возникающая в поле сил тяжести. Единица измерения веса в СИ — ньютон.

представляет собой векторную сумму двух сил: силы земного притяжения, направленной к центру Земли, и центробежной силы, возникающая из-за вращения Земли вокруг своей оси и направленная по радиусу круга широты, проходящей через рассматриваемую точку. равнодействующая силы тяготения тела (материальной точки) к Земле и центробежной силы инерции, обусловленной вращением Земли. Направление силы тяжести определяет вертикаль данного места. Силу, с которой тело притягивается к Земле под действием поля тяготения Земли, называют силой тяжести. По закону всемирного тяготения на поверхности Земли (или вблизи этой поверхности) на тело массой m действует сила тяжести F_т=GMm/R² (2.28) где М - масса Земли; R - радиус Земли.Если на тело действует только сила тяжести, а все другие силы взаимно уравновешены, тело совершает свободное падение. Согласно второму закону Ньютона и формуле (2,28) модуль ускорения свободного падения g находят по формуле g=F_т/m=GM/R²

В рамках классической механики гравитационное взаимодействие описывается законом всемирного тяготения Ньютона, который гласит, что сила гравитационного притяжения между двумя материальными точками массы m и M, разделёнными расстоянием R, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния — то есть:

Здесь G — гравитационная постоянная, равная примерно м³/(кг·с²).

Билет 11

Изучая притяжение тел по закону всемирного тяготения, мы встречаемся с гравитационным взаимодействием между телами. Это взаимодействие является одним из видов фундаментальных взаимодействий, существующих в природе. Оно осуществляется на расстоянии без непосредственного контакта между взаимодействующими телами.

Согласно представлениям материалистической науки, любое взаимодействие тел на расстоянии осуществляется посредством материальной среды, называемой полем (и поле, и вещество являются формами существования материи).Гравитационное взаимодействие между телами, описываемое законом всемирного тяготения, осуществляется посредством гравитационного поля (поля тяготения). В каждой точке поля тяготения на помещенное туда тело действует сила тяготения, пропорциональная массе этого тела. Сила тяготения не зависит от среды, в которой находятся тела.Поле тяготения обладает специфическим свойством, состоящим в том, что при переносе тела массой m из одной точки поля тяготения в другую работа силы тяготения не зависит от траектории движения тела, а зависит только от положения в этом поле начальной и конечной точек перемещения тела. Силы, обладающие подобным свойством, называют консервативными, а поле таких сил - потенциальным. Следовательно, поле тяготения является потенциальным полем, а сила тяготения - консервативной силой.Расчет показывает, что работа силы тяготения А в поле тяготения Земли определяется по формуле A=GMm(1/r₁-1/r₂), (2.27)

где m - масса тела; M - масса Земли; r₁ и r₂ - расстояния от центра Земли до начальной и конечной точек перемещения тела.

Космическая скорость (первая v₁, вторая v₂, третья v₃ и четвёртая v₄) — это минимальная скорость, при которой какое-либо тело в свободном движении сможет: v₁ — стать спутником небесного тела (то есть способность вращаться по орбите вокруг НТ и не падать на поверхность НТ). v₂ — преодолеть гравитационное притяжение небесного тела. v₃ — покинуть звёздную систему, преодолев притяжение звезды. v₄ — покинуть галактику.

Билет 12

Деформация называется упругой, если после прекращения действия внешних сил тело принимает первоначальные размеры и форму. Деформации, которые сохраня

ются в теле после прекращения действия внешних сил, называются пластическими (или остаточными). Деформации реально­го тела всегда пластические, так как они после прекращения действия внешних сил никогда полностью не исчезают

Английский физик Р. Гук (1635— 1703) экспериментально установил, что для малых деформаций относительное уд­линение e и напряжение s прямо про­порциональны друг другу:s = Ee, (21.3)где коэффициент пропорциональности Е называется модулем Юнга. Из вы­ражения (21.3) видно, что модуль Юнга определяется напряжением, вызывающим относительное удлинение, равное единице. Из формул (21.2), (21.3) и (21.1) вы­текает, что

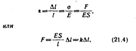где k — коэффициент упругости. Выраже­ние (21.4) также задает закон Гука, со­гласно которому удлинение стержня при упругой деформации пропорционально действующей на стержень силе.

Деформации твердых тел подчиняются закону Гука до известного предела. Связь между деформацией и напряжением пред­ставляется в виде диаграммы напряже­ний, которую мы качественно рассмотрим для металлического образца (рис. 35). Из рисунка видно, что линейная зависимость s (e), установленная Гуком, выполняется

лишь в очень узких пределах до так на­зываемого предела пропорциональности

Вычислим потенциальную энергию упругорастянутого (сжатого) стержня, кото­рая равна работе, совершаемой внешними силами при деформации:

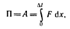
где х — абсолютное удлинение стержня, изменяющееся в процессе деформации от 0 до D l. Согласно закону Гука (21.4), F=kx=ESx/l. Поэтому

т. е. потенциальная энергия упругорастянутого стержня пропорциональна квадра­ту деформации (D l)²

Билет13

Принцип инвариантности скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерци­альных системах отсчета Принцип относительности: никакие опыты (механические, электрические, оп­тические), проведенные внутри данной инерциальной системы отсчета, не дают возможности обнаружить, покоится ли эта система или движется равномерно и прямолинейно; все законы природы ин­вариантны по отношению к переходу от одной инерциальной системы отсчета к другой

А. Эйн­штейн пришел к выводу о том, что миро­вого эфира — особой среды, которая мог­ла бы быть принята в качестве абсолют­ной системы,— не существует. Существо­вание постоянной скорости распростране­ния света в вакууме находилось в со­гласии с уравнениями Максвелла.

Таким образом, А. Эйнштейн заложил основы специальной теории относительно­сти. Эта теория представляет собой совре­менную физическую теорию пространства и времени, в которой, как и в классической ньютоновской механике, предполагается, что время однородно (см. §13), а пространство однородно (см. § 9) и изотропно (см. §19). Специальная теория относи­тельности часто называется также реляти­вистской теорией, а специфические явле­ния, описываемые этой теорией,— реляти­вистскими эффектами. Основной закон релятивистской дина­мики материальной точки имеет вид

— релятивистский импульс материальной точки

В силу однородности пространства (см. § 9) в релятивистской механике вы­полняется закон сохранения релятивист­ского импульса: релятивистский импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени. Часто во­обще не оговаривают, что рассматривают релятивистский импульс, так как если тела движутся со скоростями, близкими к с, то можно использовать только релятивист­ское выражение для импульса.Эйнштейн пришел к универсальной зависимости между полной энер­гией тела Е и его массой m:

Уравнение (40.6), равно как и (40.5), вы­ражает фундаментальный закон приро­ды — закон взаимосвязи (пропорциональ­ности) массы и энергии: полная энергия системы равна произведению ее массы на квадрат скорости света в вакууме. Отме­тим, что в полную энергию Е не входит потенциальная энергия тела во внешнем силовом поле

Билет14

Физическая величина, определяемая нормальной силой, действующей со сторо­ны жидкости на единицу площади, назы­вается давлением р жидкости:

p=DF/DS.Давление при равновесии жидкостей (газов) подчиняется закону Паскаля: давление в любом месте покоящейся жид­кости одинаково по всем направлениям, причем давление одинаково передается по всему объему, занятому покоящейся жид­костью

сила давле­ния на нижние слои жидкости будет боль­ше, чем на верхние, поэтому на тело, по­груженное в жидкость, действует выталки­вающая сила, определяемая законом Архимеда: на тело, погруженное в жид­кость (газ), действует со стороны этой жидкости направленная вверх выталкива­ющая сила, равная весу вытесненной те­лом жидкости (газа):F_А =rgV,

где r — плотность жидкости, V — объем погруженного в жидкость тела.За время D t через сечение S проходит объем жидкости Sv D t; следовательно, за 1 с через S ₁ пройдет объем жидкости S ₁ v ₁, где v ₁ — скорость течения жидкости в месте сечения S ₁. Через сечение S ₂ за 1 с пройдет объем жидкости S ₂ v ₂, где v ₂ — скорость течения жидкости в месте сечения S ₂. Здесь предполагается, что ско­рость жидкости в сечении постоянна. Ес­ли жидкость несжимаема (r=const), то через сечение S ₂пройдет такой же объем жидкости, как и через сечение S ₁, т. е.

S₁v₁ = S ₂ v ₂=const Следовательно, произведение скоро­сти течения несжимаемой жидкости на поперечное сечение трубки тока есть ве­личина постоянная для данной трубки то­ка. Соотношение называется урав­нением неразрывности для несжимаемой жидкости