Содержание задания.
По исходным данным (табл.1) вычислить координаты дополнительного пункта Р, определенного прямой засечкой. Решение выполнить для двух вариантов засечек по формуле Юнга. Найти среднюю квадратическую погрешность положения пункта Р.
| Исходные пункты | координаты | углы | |
| х | у | ||
| А | 10370,19 | 5440,44 | β1=54 059 /33// -β2=75 039 /02// β3 = 47 037 /09// -β4 =390 45/ 32// mβ =10// |
| В | 8945,58 | 4584,95 | |
| С | 6422,25 | 5801,90 |
табл. 1
По исходным данным табл.2 вычислить координаты дополнительного пункта Р, определяемого обратной засечкой. Решение выполнить для двух вариантов засечек по формуле Кнейсселя. Найти среднюю погрешность положения пункта Р.
табл.2
| Исходные пункты | координаты | углы | |
| х | у | ||
| А | 5870,75 | 7315,37 | γ1=54 059 /33// γ2=75 039 /02// γ3 = 47 037 /09// mβ =10// |
| В | 2000,14 | 3100,48 | |
| С | 8142,14 | 2840,31 |
Указания и порядок задания
1. Решение прямой засечки
1. Решение выполнить по формуле Юнга на основе исходных данных приведенных в таблице 1. Координаты пункта Р вычисляют дважды (на 1 и 2 треугольник).
2.Вычисление проводят по Формуле Юнга для треуг.-ка АВР
для треуг.-ка ВРС
3.Вычесления по формулам выполнять в следующей таблице 3.
4.После определения координат точки Р по двум вариантам сделать оценку точности засечки. Для этого вычисляют средние квадратические погрешности М1 и М2. (в м,) положения пункта Р используя формулы:
М1 = 
М 2 = 
mβ -средняя квадратическая измерения углов погрешность (берется из таблицы 1.) сек.
SA, SB, Sc - расстояние от точки Р до соответствующих исходных пунктов
А, В, и С. γ =∠АРВ, γ1 = ∠ВРС
5.Для определения расстояний, на листе бумаги построить координатные оси(ось У и ось Х) в масштабе 1: 50000 на лист нанести по координатам исходные пункты А, В,С и точку Р. По построенному чертежу графически определить расстояние SА ,S В , SС.
|
|
6. Вычислить величину r по формуле:
r = 
Х Р1 и У Р1 - координаты точек полученные из 1 варианта.
7. Величину r сравнить с величиной М r, вычисленной по формуле:
М r = 
Если вычисление выполнены правильно то будет: r ˂ 3 Мr
8. Вычислить окончательные значение координат точки Р, как среднее арифметическое.
| № тр-ка | пункты | Измеренные углы | ctg β1 ctg β2 ctg β1 + ctg β2 | Координаты Х м, | Координаты У м, |
| вариант | А | 540 59/ 33// | 0,700403 | 10370,19 | 5440,44 |
| В | 750 39/ 02// | 0,255820 | 8945,58 | 4584,95 | |
| Р | - | 0,956223 | 8431,95 | 6308,64 | |
| 2 вариант | В | 470 37/ 09// | 0,912510 | 8945,58 | 4584,95 |
| С | 390 45/ 32// | 1,201991 | 6422,25 | 5801,90 | |
| Р | - | 2,114501 | 8432,17 | 6303,47 |
9. Вычислить среднюю квадратическую погрешность среднего из двух положенийпункта Р по формуле: М = 
табл.3
Решение обратной засечки.
1. Решение выполнять по формуле Кнейссля на основе исходных данных приведенные в таблице 2. координаты пункта следует вычислить дважды.
2. Формула Кнейссла имеет вид:
К1 = (УВ - УА) . ctg γ1 - (Х В - ХА); К2 = (Х В-ХА). ctg γ1 - (УВ - УА);
К3 = (Ус - УА) . ctg γ2 - (Х с - ХА); К4 = (Ус - УА) . ctg γ2 - (Х с - ХА);
С = 
; Δ У = 
= 
; Δ Х = С .Δ У
Х р= ХА +ΔХ Ур = УА + ΔУ
3. Для варианта 2 (исходные пункты А, В, Д.)
К1 = (УВ - УА) . ctg γ1 - (Х В - ХА); К2 = (Х В-ХА). ctg γ1 - (УВ - УА);
К3 = (Уд - УА) . ctg γ3 - (Х д - ХА); К4 = (Уд - УА) . ctg γ3 - (Х д- ХА);
С = ; Δ У = 
= ; Δ Х = С .Δ У
Х р= ХА +ΔХ Ур = УА + ΔУ
4. В каждом варианте контролем правильности вычислений служит равенство величин: К2 - СК1 = К4 - СК3
5. После вычисления координат точки Р вычислить средние квадратические погрешности.
|
|
М1 = 
М 2 = 
М 1 = 
= 0,14
М 2 = 
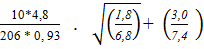=0,12
Пример решения обратной засечки. вариант 1.
| γ1 | 117 012 /42 // | К1 | +6037,86 | |
| γ2 | 21 40 14 /46// | К3 | -8844,87 | |
| ctg γ1 | - 0, 514189 | |||
| ctg γ1 | +1, 468915 | К1 -К3 | +14882,73 | |
| ХВ | 2000,14 | К2 | -2224,67 | |
| ХС | 8142,14 | К4 | -1138,59 | |
| ХА | 5870,75 | |||
| Х В- ХА | -3870,61 | К2 -К4 | -1086,08 | |
| ХС -ХА | +2271,89 | С, С2 | -072975 | 0,005325 |
| ХС -ХВ | +6142,00 | К2 -СК1 | -1784,06 | |
| УВ | +3100,48 | К4 -СК3 | -1784,05 | |
| УС | 2840,31 | Δ У | -1774,61 | |
| УА | 7315,37 | УА | 7315,37 | |
| Ур | 5540,76 | |||
| УВ-УА | -4214,89 | ΔХ | +129,50 | |
| УС-УА | -4475,06 | ХА | 5870,75 | |
| УС-УВ | -260,17 | Хр | 6000,25 |
Пример решение обратной засечки вариант 2.
| γ1 | 117 012 /42 // | К1 | +6037,86 | |
| γ3 | 2630 09 /00// | К3 | -3359,38 | |
| ctg γ1 | - 0, 514189 | |||
| ctg γ3 | +0,120130 | К1 -К3 | +9397,24 | |
| ХВ | 2000,14 | К2 | -2224,67 | |
| ХД | 9000,16 | К4 | -1538,41 | |
| ХА | 5870,75 | |||
| Х В- ХА | -3870,61 | К2 -К4 | -1086,08 | |
| ХД -ХА | +3129,41 | С, С2 | -0,073028 | 0,005333 |
| ХД -ХВ | +7000,03 | К2 -СК1 | -1783,74 | |
| УВ | +3100,48 | К4 -СК3 | -1783,74 | |
| УД | 5401,02 | Δ У | -1774,28 | |
| УА | 7315,37 | УА | 7315,37 | |
| Ур | 5541,06 | |||
| УВ-УА | -4214,89 | ΔХ | +129,57 | |
| УД-УА | -1914,35 | ХА | 5870,75 | |
| УС-УВ | -2300,54 | Хр | 6000,32 |
Оценка точности засечки.
r = 
=0,34м,
М r = 
=0,18 м,
М = 
=0,09 м,
Контроль: r < 3 М r (0,34м < 0, 54)
Окончательные координаты точки Р
Хр = 6000,28 Ур = 5540,92 М=0,09
mγ = средняяквалратическая погрешность измерения углов γ,сек.
SА, Sв , SС, SД - расстояния между точкой Р и исходными пунктами А, В,С,Д,км.
SАВ, SВС, SВД, - расстояние между пунктами.
6. Для определения расстояния и углов ∠ АВС,∠АВД на листе бумаги
построить координатные оси в масштабе 1: 100000 нанести на лист по
|
|
координатам исходные пункты А, В, С. д. и точку Р.
Контрольные вопросы:
1. Назовите основные случаи определения дополнительных пунктов?
2. Что такое "Передача координат с вершины знака на землю"?
3.Когда при решение прямой засечки применяют формулу Юнгаи когда формулу Гаусса?
4. Как проконтролировать определение координат точки Р методом прямой
засечки, если дано лишь два исходных пункта.