1. Ввести исходные данные в файл программы Microsoft Exсel. Данные измерений записать в столбец А. Отсортировать данные в порядке возрастания.
2. Построить дискретный вариационный ряд. Для этого составить таблицу из четырех столбцов, где в первый столбец записать варианты x i (различные значения признака, наблюдающиеся у членов совокупности). Число, показывающее сколько раз встречается вариант, называется частотой n i. Подсчитать частоты и внести во второй столбец таблицы. Посчитать сумму частот Σ n i. В третий столбец таблицы записывают
вычисленные частости w i. Посчитать сумму частостей Σ w i. Результат должен быть равен единице. В четвертом столбце считаются накопленные частости w n.i., т.е. сумма накопленной частости предыдущего варианта и частости текущего.
3. По результатам таблицы построить полигон и кумулятивную
кривую. Для построения полигона по оси X откладывают значения вариантов, по оcи Y – значения частостей и находятся точки с координа-
3. По результатам таблицы построить полигон и кумулятивную кривую. Для построения полигона по оси X откладывают значения вариантов, по оcи Y – значения частостей и находятся точки с координатами (x i; w i).
При построении кумулятивной кривой по оси X откладываются значения вариантов, по оси Y – значения накопленных частостей. Находятся точки с координатами (x i; w н.i).
4. Рассчитываются показатели вариации:
Размах вариации – разность между наибольшим X max и наименьшим X min вариантами:
· R = X max – X min. (1.1)
Средняя арифметическая вариационного ряда – сумма произведений всех вариантов x i на соответствующие им частоты n i, деленная на сумму частот Σ n i:
Х=  (1.2)
(1.2)
В электронных таблицах Microsoft Exсel встроенная функция для расчета средней арифметической называется «СРЗНАЧ».
Дисперсия D вариационного ряда – средняя арифметическая квадратов отклонений от их средней:
 (1.3)
(1.3)
.
В электронных таблицах Microsoft Exсel встроенная функция для расчета дисперсии называется «ДИСПР».
Среднее квадратическое отклонение σ – арифметическое значение квадратного корня из дисперсии

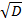 (1.4)
(1.4)
В электронных таблицах Microsoft Exсel встроенная функция для расчета среднеквадратического отклонения называется «СТАНДОТКЛОН».
Коэффициент вариации V:
·  (1.5)
(1.5)
Дисперсия и среднеквадратическое отклонение характеризуют рассеяние признака от средней величины. Коэффициент вариации показывает, насколько средняя арифметическая представительна.
Сделать вывод по работе.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
(ДГТУ)
Факультет Автоматизации, мехатроники и управления
Кафедра Робототехники и мехатроники
Методическое руководство по выполнению практического занятия №4
Исследование интервального вариационного ряда.
Ростов-на-Дону
2016 г.
ИССЛЕДОВАНИЕ ИНТЕРВАЛЬНОГО
ВАРИАЦИОННОГО РЯДА
Цель работы: научиться отличать дискретный и интервальный вариа-
ционные ряды, по данным измерений построить интервальный вариационный ряд, рассчитать показатели вариации интервального вариационного ряда.
Исходные данные: варианты заданий приведены в приложении 2. Работу выполнить в программе Microsoft Exсel.
Интервальным называется вариационный ряд, в котором значения признака могут отличаться друг от друга на сколь угодно малую величину. В непрерывном вариационном ряду возможные значения признака задаются интервалами. В общем виде он выглядит следующим образом: Значение признака Вес
α 1 – α 2 n 1
α 2 – α 3 n 2
… …
α m – α m+1 n m
Разности k 1 = α 2 – α 1; k = α 3 – α 2, и т.д. называются интервальными разностями