ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
Пусть на тело действует произвольная система сил 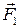 ,
, 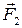 , …,
, …, 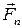 , расположенных в пространстве (рис. 1, а). Возьмем произвольную точку
, расположенных в пространстве (рис. 1, а). Возьмем произвольную точку 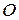 , которую назовем центром приведения, и по аналогии, как и для плоской системы, приведем все эти силы к центру
, которую назовем центром приведения, и по аналогии, как и для плоской системы, приведем все эти силы к центру 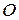 (рис. 1, б). В результате в центре
(рис. 1, б). В результате в центре 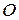 получаем:
получаем:
· систему сходящихся сил, складывая которые получаем главный вектор системы  ;
;
· пространственную систему присоединенных пар, вектора-моменты которых равны:
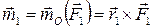 ,
, 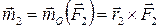 , …,
, …, 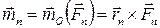 ;
;
Сложим геометрически вектора-моменты присоединенных пар. В результате система пар заменится одной парой, вектор-момент которой будет равен
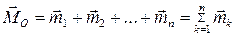 или
или 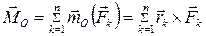 .
.
Величина 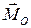 , равная геометрической сумме векторов-моментов всех сил относительно центра
, равная геометрической сумме векторов-моментов всех сил относительно центра 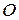 , называется главным моментом системы сил относительно этого центра.
, называется главным моментом системы сил относительно этого центра.
рис. 1
Определим проекции этих двух векторов на координатные оси:
 ,
,
 ,
,
 ,
,
 .
.
Направление главного вектора  определяют направляющие косинусы:
определяют направляющие косинусы:
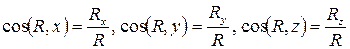 .
.
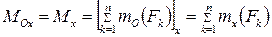 ,
, 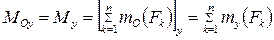 ,
,
 ,
,
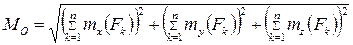 .
.
Направление главного момента 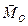 определяют направляющие косинусы:
определяют направляющие косинусы: 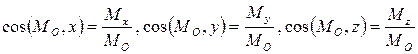 .
.
Рассмотрим теперь, к каким простейшим видам можно привести пространственную систему сил.
1. Если для данной системы сил 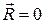 , а
, а  , то она приводится к одной паре с моментом
, то она приводится к одной паре с моментом 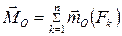 . Причем в этом случае величина
. Причем в этом случае величина 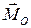 не зависит от центра приведения, так как иначе мы получили бы, что одна и та же система сил заменяется разными, неэквивалентными друг другу, парами, что невозможно.
не зависит от центра приведения, так как иначе мы получили бы, что одна и та же система сил заменяется разными, неэквивалентными друг другу, парами, что невозможно.
2. Если для данной системы сил  , то здесь появляются следующие варианты приведения:
, то здесь появляются следующие варианты приведения:
а)  ,
, 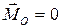 . В этом случае система сразу заменяется равнодействующей, которая в данном варианте будет равна главному вектору системы и проходит через точку
. В этом случае система сразу заменяется равнодействующей, которая в данном варианте будет равна главному вектору системы и проходит через точку 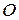 ;
;
б)  ,
,  и
и 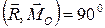 . В этом случае система также заменяется равнодействующей, которая будет равна главному вектору системы, но проходить она будет не через точку
. В этом случае система также заменяется равнодействующей, которая будет равна главному вектору системы, но проходить она будет не через точку 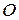 , а через точку
, а через точку 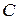 . Определим положение точки
. Определим положение точки 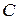 . Пусть система приводится к главному вектору
. Пусть система приводится к главному вектору 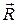 и главному моменту
и главному моменту 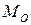 относительно центра
относительно центра 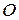 (рис. 2, а).
(рис. 2, а).
Пару сил изобразим силами  и
и 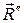 , причем эти силы подбираем таким образом, чтобы выполнялись равенства:
, причем эти силы подбираем таким образом, чтобы выполнялись равенства:  ,
, 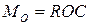 (рис. 2, б). Затем отбрасываем силы
(рис. 2, б). Затем отбрасываем силы 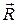 и
и 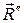 как уравновешенные и получаем, что система заменяется равнодействующей
как уравновешенные и получаем, что система заменяется равнодействующей 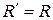 , но проходящей через точку
, но проходящей через точку 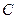 (рис. 7.2, Положение точки
(рис. 7.2, Положение точки 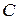 определится соотношением
определится соотношением  .
.
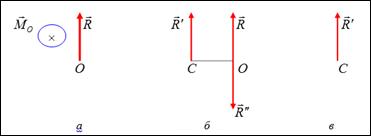
рис. 2
3. Приведение к динамическому винту. Если в результате приведения системы получили главный вектор и главный момент, причем угол между ними либо 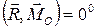 , либо
, либо 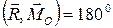 , т.е. эти вектора коллинеарные, то такая система называется динамическим винтом.
, т.е. эти вектора коллинеарные, то такая система называется динамическим винтом.
Покажем, что если угол 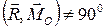 , то систему всегда можно привести к динамическому винту. Рассмотрим такой случай (рис. 3, а). Разложим
, то систему всегда можно привести к динамическому винту. Рассмотрим такой случай (рис. 3, а). Разложим 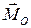 на две взаимно перпендикулярные составляющие:
на две взаимно перпендикулярные составляющие: 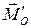 , которая направлена, перпендикулярна плоскости
, которая направлена, перпендикулярна плоскости 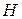 , и
, и 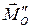 , которая лежит в плоскости
, которая лежит в плоскости  .
.
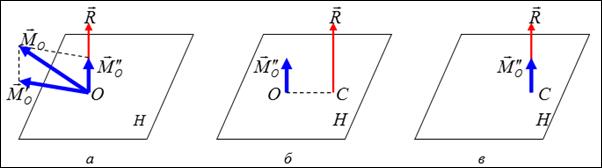
рис. 3
Заменяя вектора  и
и 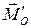 по процедуре, описанной ранее, получаем вектор
по процедуре, описанной ранее, получаем вектор 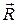 , но проходящий не через точку
, но проходящий не через точку 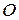 , а через точку
, а через точку 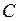 (рис. 3, б). Вектор
(рис. 3, б). Вектор 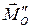 можно свободно переносить в плоскости
можно свободно переносить в плоскости 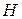 , используя свойства пар сил. Поэтому переносим
, используя свойства пар сил. Поэтому переносим 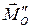 параллельно самому себе в точку
параллельно самому себе в точку 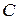 . В результате получаем два коллинеарных вектора
. В результате получаем два коллинеарных вектора 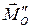 и
и 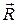 , которые и образуют динамический винт (рис. 3, в).
, которые и образуют динамический винт (рис. 3, в).
4. Приведение к равновесию. Если для данной системы сил 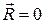 и
и 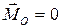 , то она находится в равновесии.
, то она находится в равновесии.
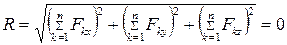 ,
,
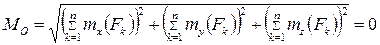
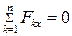 ,
, 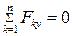 ,
,  ,
,
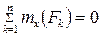 ,
, 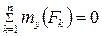 ,
,  .
.
Получили шесть условий равновесия: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из координатных осей, а также суммы моментов этих сил относительно каждой из координатных осей были равны нулю.
Задача.
Дано. Прямоугольная дверь  , имеющая вертикальную ось вращения
, имеющая вертикальную ось вращения  , открыта на угол
, открыта на угол  и удерживается в этом положении двумя веревками, из которых одна,
и удерживается в этом положении двумя веревками, из которых одна,  , перекинута через блок
, перекинута через блок 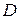 и натягивается грузом
и натягивается грузом 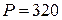
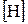 , а другая,
, а другая,  , привязана к точке
, привязана к точке 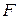 пола. Вес двери
пола. Вес двери 
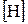 , ее размеры – ширина
, ее размеры – ширина 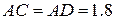
 , высота
, высота 
 . Пренебрегая трением на блоке, определить натяжение
. Пренебрегая трением на блоке, определить натяжение 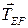 веревки
веревки  , а также реакции цилиндрического шарнира в точке
, а также реакции цилиндрического шарнира в точке  и подпятника в точке
и подпятника в точке  .
.
 Решение. Делаем переход от общего вида (рис. 4, а) к расчетной схеме (рис. 4, б). Выделяем в рассмотрение дверь
Решение. Делаем переход от общего вида (рис. 4, а) к расчетной схеме (рис. 4, б). Выделяем в рассмотрение дверь  , показывая активные силы и реакции со стороны отброшенных связей. В точке
, показывая активные силы и реакции со стороны отброшенных связей. В точке  стоит опора – подпятник, который препятствует любому отрыву двери от оси вращения, т.е. составляющие реакции будут направлены вдоль осей
стоит опора – подпятник, который препятствует любому отрыву двери от оси вращения, т.е. составляющие реакции будут направлены вдоль осей 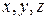 . В точке
. В точке  реакции будут направлены только вдоль осей
реакции будут направлены только вдоль осей 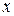 и
и 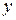 , так как при желании дверь можно снимать с петель. Кроме того, для пространственных схем выбор осей координат имеет важное значение при составлении условий равновесия. Исходя из свойств момента силы относительно оси, сила не будет создавать момент относительно оси, если она пересекает ось либо ей параллельна.
, так как при желании дверь можно снимать с петель. Кроме того, для пространственных схем выбор осей координат имеет важное значение при составлении условий равновесия. Исходя из свойств момента силы относительно оси, сила не будет создавать момент относительно оси, если она пересекает ось либо ей параллельна.
Таким образом, оси лучше проводить так, чтобы как можно больше сил пересекало эти оси либо были им параллельны.
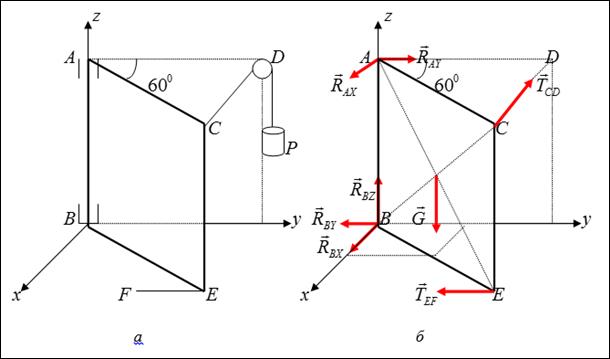
рис. 4
Учитываем, что 
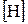 ,
, 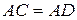 и угол
и угол  , значит, треугольник
, значит, треугольник 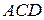 – равносторонний. Тогда условия равновесия:
– равносторонний. Тогда условия равновесия:
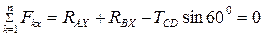 ,
, 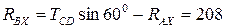
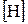 ,
,
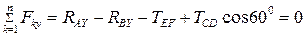 ,
, 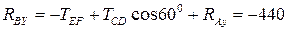
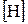 ,
,
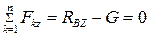 ,
, 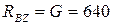
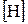 .
.
Теперь рассмотрим уравнения моментов. Относительно оси 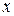 моменты не будут создавать силы
моменты не будут создавать силы 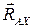 ,
, 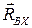 ,
, 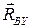 ,
, 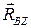 ,
, 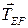 , так как они по отношению к ней либо параллельны, либо пересекают ось
, так как они по отношению к ней либо параллельны, либо пересекают ось 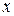 .
.
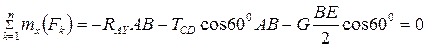 ,
, 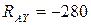
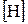 .
.
Относительно оси 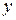 моменты не будут создавать силы
моменты не будут создавать силы 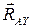 ,
, 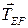 ,
, 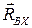 ,
, 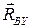 ,
, 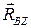 , так как они по отношению к ней либо параллельны, либо пересекают ось y.
, так как они по отношению к ней либо параллельны, либо пересекают ось y.
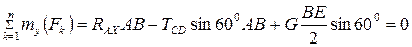 ,
, 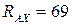
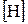 .
.
Относительно оси z моменты не будут создавать силы 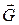 ,
, 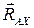 ,
, 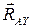 ,
, 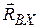 ,
, 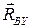 ,
, 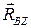 , так как они по отношению к ней либо параллельны, либо пересекают ось z.
, так как они по отношению к ней либо параллельны, либо пересекают ось z.
 ,
, 
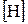 .
.
Ответ: 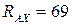
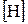 ,
, 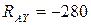
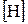 ,
, 
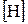 ,
, 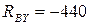
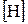 ,
, 
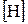 ,
, 
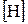 . Реакции
. Реакции 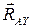 ,
, 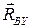 получены со знаком «-», который указывает на то, что эти реакции направлены в обратную сторону.
получены со знаком «-», который указывает на то, что эти реакции направлены в обратную сторону.