Лекция № 5.
Преобразование чертежа. Способ замены плоскостей проекций.
Цель лекции: познакомиться с одним из способов замены преобразования чертежа – способом замены плоскостей проекций, для решения метрических задач.
Суть способа.
При решении метрических задач (определение размеров изображенных фигур) могут встретиться трудности, если заданные проекции не подвергнуть специальным преобразованиям. Одним из способов преобразования чертежа является способ замены плоскостей проекций. Суть способа заключается в том, что вводится новая плоскость П4, располагаемая перпендикулярно одной из существующих, а по отношению к фигуре, таким образом, чтобы прямая или плоскость при проекции на эту плоскость заняли частное положение.
На рис. 1 показана точка А, заданная в системе плоскостей проекций П1П2. Заменим плоскость П2 новой вертикальной плоскостью П4 и построим проекцию точки А на эту плоскость. Так как плоскости проекций П2 и П4 являются вертикальными то координата z точки А остается неизменной. При этом горизонтальная плоскость проекций П1 остается общей для «старой» и «новой» систем. Следовательно, расстояние от новой проекции точки А на плоскости П4 до новой оси x14 равно расстоянию от заменяемой проекции (А2) до оси x12.
А2А12 = А4А14
При этом точка А4 определена как основание перпендикуляра, опущенного из А на П4.
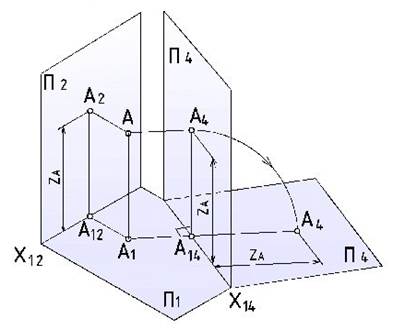
Рисунок 1 – Геометрическая схема способа замены плоскостей проекций.
Последовательный переход от одной системы плоскостей проекций к другой необходимо осуществлять, выполняя следующее правило: расстояние от новой проекции точки до новой оси (от А4 до х14 (рис. 1)) должно равняться расстоянию от преобразуемой (заменяемой) проекции точки до предыдущей оси (от А2 до х14 (рис.1)).
Для получения эпюра плоскость П4 вращением вокруг x14 совмещается с П1. Совместится с П1 и новая проекция А4 точки А, лежащая на перпендикуляре к новой оси x14 с горизонтальной проекции А1.
Аналогично можно заменить горизонтальную плоскость проекций П1 плоскостью П4, перпендикулярной П2.
Решение метрических задач.
Задача. Определить Н.В. отрезка АВ прямой общего положения.
Введем новую плоскость П4 отвечающую двум условиям: П4 ┴ П1 и П4 ║АВ, следовательно x14 ║A1B1 (рис. 2). От точек А1 и В1 проводят линии перпендикулярные x14. Откладывая на этих линиях расстояния равные zA и zB получаем проекцию А4В4 отрезка АВ на плоскости проекций П4. На плоскость П4 без искажения проецируется отрезок АВ и угол α – угол наклона отрезка АВ к горизонтальной плоскости проекций П1. Поскольку П4 ║АВ, А4В4 есть натуральная величина отрезка АВ.
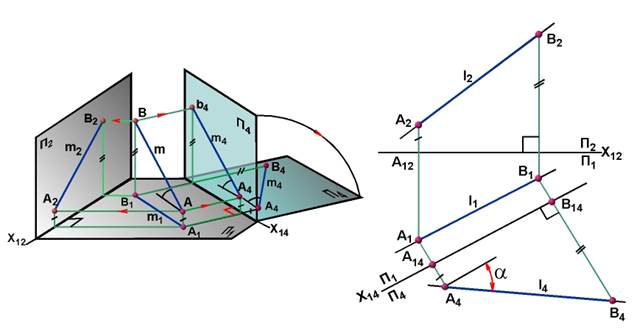
Рисунок 2 – Определение Н.В. прямой общего положения
Задача. Определить натуральную величину отрезка прямой общего положения АВ и расстояние от т. К до данного отрезка прямой (рис. 3).
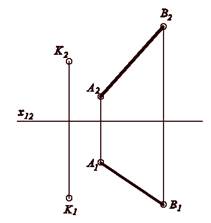
Рисунок 3 – Графическая часть задачи 1
Решение задачи показано на видео.
Задача. Определить Н.В. треугольного отсека АВС плоскости общего положения.
Решение данной задачи требует двойной замены плоскостей проекций (рис. 4). Смысл первой замены П2 на П4 заключается в преобразовании плоскости треугольника в проецирующую.
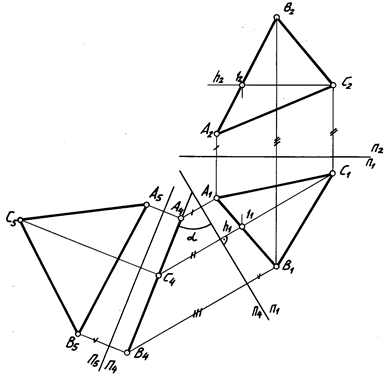
Рисунок 4 – определение Н.В. отсека плоскости общего положения
Для этого новую плоскость проекций необходимо расположить перпендикулярно треугольнику АВС и одной из плоскостей проекций. Значит новая плоскость должна быть перпендикулярна линии пересечения заданной плоскости с одной из плоскостей проекций. Направление линии пересечения заданной плоскости и одной из плоскостей проекций можно установить с помощью главной линии плоскости (горизонтали или фронтали). Поэтому в заданной плоскости проводим горизонталь С1. Расположив П4 ┴ С1 обеспечиваем выполнение двух условий: новая плоскость П4 перпендикулярна П1 и плоскости треугольника. Новую ось x14 проводят под прямым углом к С111. Проведя через горизонтальные проекции вершин треугольника прямые, перпендикулярные новой оси, откладываем на этих прямых от x14 отрезки равные zA, zB, zC. Таким образом получаем новую проекцию А4В4С4 треугольника АВС представляющую собой прямую линию. На плоскость П4 без искажения проецируется угол α, образованный треугольником с плоскостью П1.
Второй этап решения задачи заключается в переходе от системы П1П4 к системе П4П5. Новая плоскость П5 устанавливается параллельно треугольнику, следовательно новая ось x45 на чертеже проводится параллельно прямой, на которой расположены точки А4, В4 и С4. Через указанные точки проводят перпендикуляры к новой оси и откладывают на них расстояния от оси x45 равные расстоянию от оси x14 до заменяемых точек А1, В1 и С1.
Полученная проекция А5В5С5 определяет натуральную величину треугольника.
Задача. Определить расстояние от т. К до отсека плоскости АВС и натуральную величину отсека плоскости (рис. 5)
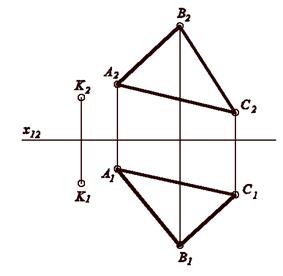
Рисунок 5 – Графическая часть задачи 2.
Решение задачи показано на видео.
Все задачи, решаемые преобразованием, сводятся к 4 основным задачам:
задача 1 - преобразовать чертеж прямой общего положения в чертеж прямой уровня;
з адача 2 - преобразовать чертеж прямой общего положения в чертеж проецирующей прямой;
задача 3 - чертеж плоскости общего положения преобразовать в чертеж проецирующей плоскости;
задача 4 - чертеж плоскости общего положения преобразовать в чертеж плоскости уровня.