Любезнов Геннадий Александрович
учитель математики
МБОУ «СОШ №1 г. Лесосибирска»
Цель: познакомить учащихся 11 класса с различными методами решения текстовых задач номер 11 «на смеси, сплавы и растворы» из профильного уровня ЕГЭ.
Способы решения задач (без использования химических формул):
· с помощью таблиц;
· с помощью схемы;
· арифметическим способом;
· алгебраическим способом;
· с помощью графика;
· Правило креста.
Решение задач с помощью таблицы:
Задача. Сколько нужно добавить воды в сосуд, содержащий 200 г 70 % -го раствора уксусной кислоты, чтобы получить 8 % раствор уксусной кислоты?
Решение:
| Наименование веществ, смесей | Процентное содержание вещества | Масса раствора (г) | Масса вещества (г) |
| Исходный раствор | 70 % = 0,7 | 0,7·200 | |
| Воды долили | - | х | - |
| Новый раствор | 8 % = 0,08 | 200 + х | 0,08(200 + х) |
Так как подливали только воду, масса уксусной кислоты в растворе не изменилась. Составляем уравнение:
0,08(200 + х) = 0,7·200
16 + 0,08х = 140
0,08х = 124
х = 1550
Ответ:1,55 кг воды.
Решение задач с помощью схемы:
Задача. Сколько нужно добавить воды в сосуд, содержащий 200 г
70 % -го раствора уксусной кислоты, чтобы получить 8 % раствор уксусной кислоты?
Решение:
Пусть в сосуд долили х литров воды. Получаем схему:
Задача. Имеется два сплава меди и свинца. Один сплав содержит 15% меди, а другой 65% меди. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?
Решение:
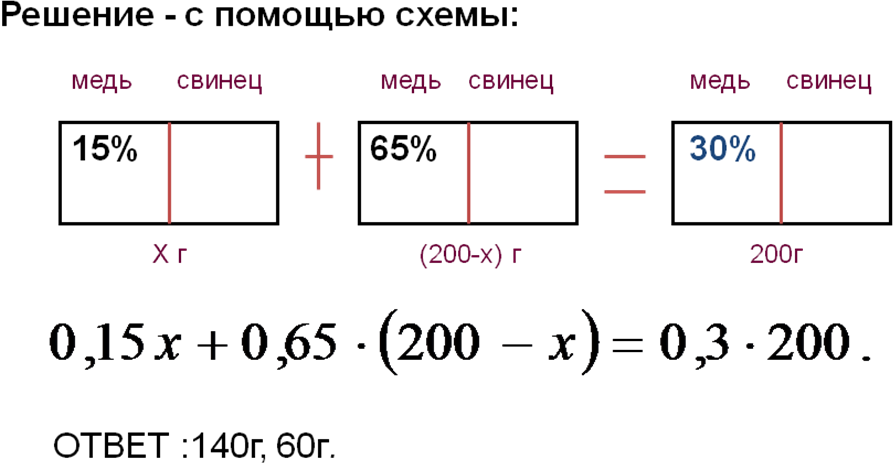
Решение задач арифметическим способом:
Задача. При смешивании 5% -ного раствора кислоты с 40% -ным раствором кислоты получили 140 г 30% -ного раствора. Сколько грамм каждого раствора надо было взять?
Решение:
Рассмотрим пары 30 и 5; 30 и 40. В каждой паре их большего числа вычтем меньшее и результат запишем в конце соответствующей чёрточки. Получилась схема:
Из неё делается заключение, что 5% раствора следует
взять 10 частей, а 40 % - 25 частей. Узнав, сколько
приходится на одну часть 140: (10+25) = 4 г., получаем,
что 5% - ного раствора необходимо взять 40г,
а 40% -ного -100 г
Ответ: 40 г - 5% -ного раствора и 100г - 40% - ного раствора.
Задача: Первый сплав содержит 10% меди, второй – 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Решение:
Пусть масса первого сплава равна m кг,
тогда масса второго сплава m+3 кг.
Заполним таблицу:
Отношение полученных масс равно отношению
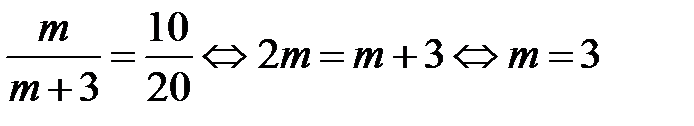долей, в которых требуется сплавлять исходные
сплавы. Поэтому кг.
Тогда масса второго сплава равна 6 кг, а масса третьего сплава равна 9 кг.
Ответ: 9.
Решение задач алгебраическим способом:
Задача: Смешали 30%-й раствор соляной кислоты с 10%-ым раствором и получили 600 г 15%-го раствора. На сколько граммов масса первого раствора меньше массы второго?
Решение:
Обозначим x массу первого раствора,
тогда масса второго (600 - x).
Составим уравнение:
0,3x + 0,1* (600 - x) = 600 * 0,15
0,3х + 60 - 0,1х = 90
0,2х = 30
x = 150 (г.) масса 1 раствора
600 - 150 = 450 (г.) масса 2 раствора
450-150 = 300 (г.)
Ответ: на 300 г. масса 1 раствора меньше массы 2 раствора
Решение задач способом креста:
Задача: Смешали некоторое количество 15–процентного раствора некоторого вещества с таким же количеством 19–процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение:
| 19-х | ||
| х | ||
| Х-15 |
Запишем исходные концентрации в левый столбец таблицы, искомую полученную концентрацию х запишем в центральный столбец. Правый столбец таблицы заполним разностями исходных и полученной концентрации, вычитая из
большей концентрации меньшую.
Отношение полученных разностей
равно отношению долей, в которых требуется смешать растворы для получения из растворов исходной концентрации раствора с требуемой концентрацией. Так как объемы смешиваемых растворов равны, имеем:
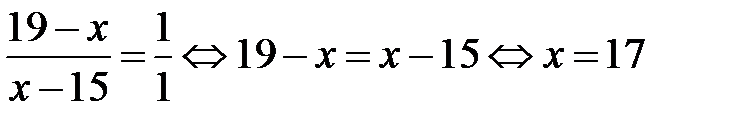
Ответ: 17.
Решение задач геометрическим способом:
Задача: Смешали 30%-й раствор соляной кислоты с 10%-ым раствором и получили 600 г 15%-го раствора. На сколько граммов масса первого раствора меньше массы второго?
Решение:
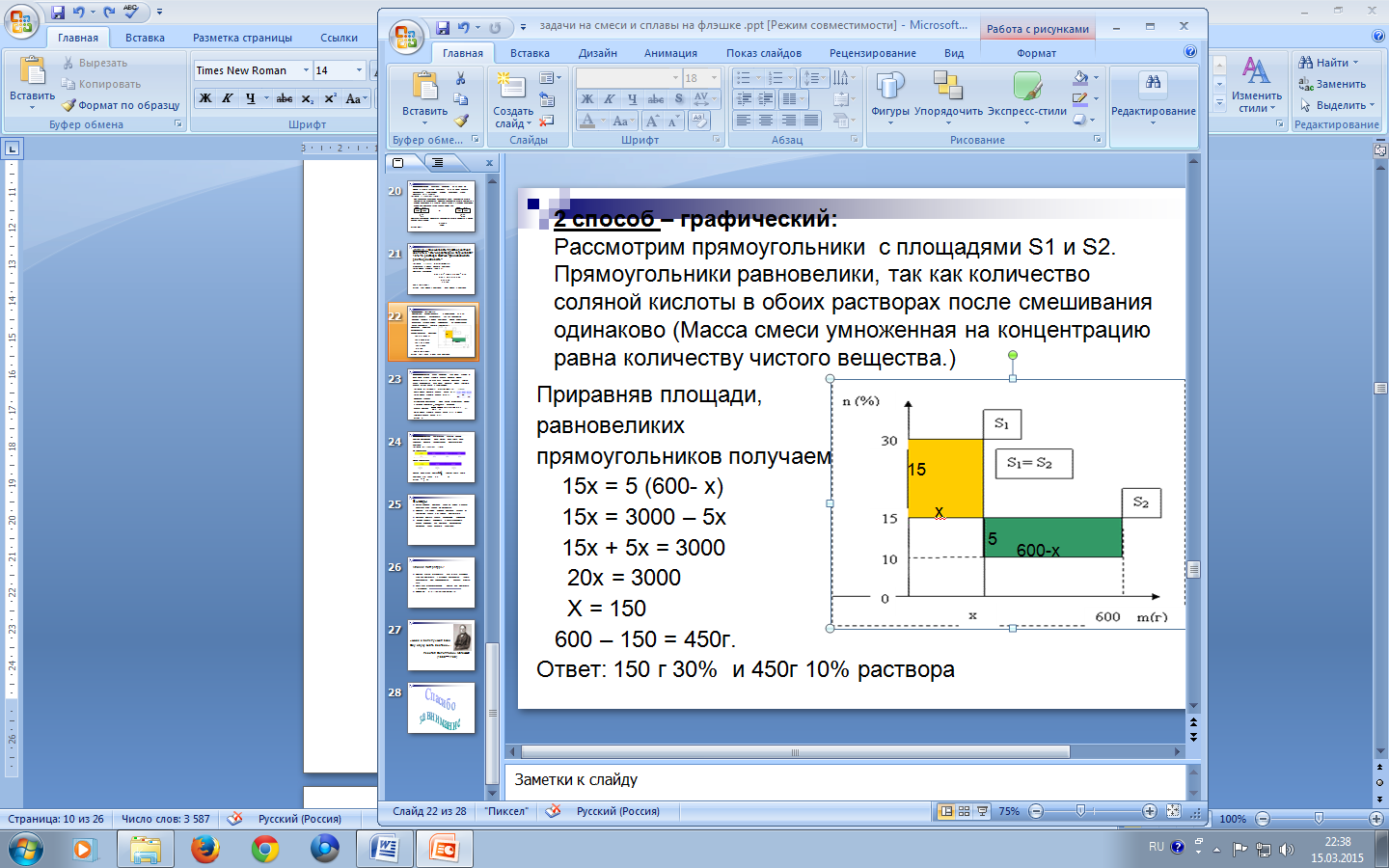
Рассмотрим прямоугольники с площадями S1 и S2. Прямоугольники равновелики, так как количество соляной кислоты в обоих растворах после смешивания одинаково (Масса смеси умноженная на концентрацию равна количеству чистого вещества.)
Приравняв площади, равновеликих прямоугольников получаем
15x = 5 (600- x)
15х = 3000 – 5х
15х + 5х = 3000
20х = 3000
Х = 150
600 – 150 = 450г.
450-150 = 300 (г.)
Ответ: на 300 г. масса 1 раствора меньше массы 2 раствора