Министерство образования и науки РФ
БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
“ВОЕНМЕХ” им. Д.Ф. Устинова
Кафедра ракетостроение
Отчет по лабораторной работе №2
Компьютерное обеспечение технических решений
Выполнил: Сафиулин Р.Т.
Группа: КВ-61
Проверил: Степанов М.М.
Вариант №12
ЛАБОРАТОРНАЯ РАБОТА №2
Решение дифференциальных уравнений в частных производных эллиптического типа методом конечных разностей
(на примере двумерного уравнения Лапласа)
Цель работы
· изучение конечно-разностных методов решения дифференциальных уравнений в частных производных эллиптического типа на примере двумерного уравнения Лапласа;
· освоение наиболее распространенных простейших разностных схем решения этого уравнения;
· исследование свойств разностных схем;
· изучение методов решения получающихся систем линейных алгебраических уравнений;
· изучение возможных алгоритмов реализации данных методов на ЭВМ;
Краткие сведения из теории
3.2.1. Двумерным уравнением Лапласа называется следующее дифференциальное уравнение в частных производных второго порядка эллиптического типа:
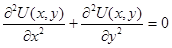(3)
Это уравнение часто встречается в приложениях и описывает целый ряд важных физических процессов:
§ напряжения, возникающие при упругом кручении цилиндрического стержня;
§ распределение потенциалов (или электрических напряжений) на проводящей плоскости при задании потенциала на ее границе;
§ стационарные (установившиеся) поля температур в двумерном твердом теле;
§ дозвуковое (потенциальное) течение газа и т.д.
Для корректной постановки задачи необходимо задание соответствующих граничных условий. Если граничные условия задаются в виде
U(x,y)│s = f(x,y), где S - граница рассматриваемой области, (4)
то задача носит название «задачи Дирихле».
Используемые методы
«Прямые» методы решения уравнения Лапласа
В данной лабораторной работе для решения указанного уравнения в качестве «прямого» метода предлагается использовать схему Рунге (другое название «пятиточечная схема»). Будучи примененная к уравнению Лапласа в сочетании с последующим использованием для решения получающейся системы линейных алгебраических уравнений итерационного метода Гаусса - Зайделя, она получила название «метода Либмана». Именно метод Либмана используется в данной лабораторной работе.
Схема Рунге (пятиточечная схема)
Простейшая пятиточечная схема выглядит следующим образом:
(5)
Модифицированное уравнение (дифференциальное приближение) этой схемы имеет следующий вид:
Схема имеет второй порядок аппроксимации. Абсолютно согласована. Превалируют диссипативные ошибки.
При ∆x=∆y разностные уравнения имеют вид:
(6)
Уравнение (5) или (как в данной лабораторной работе) уравнение (6) записывается для всех узлов сетки, в которых величина U(i,j) неизвестна, т.е. для всех ее «внутренних» узлов. Если задача решается в квадрате, каждая сторона которого разбита N точками на (N-1) отрезков, то (при граничных условиях Дирихле) в каждом из внутренних узлов должно удовлетворяться разностное уравнение (5) или (6). При этом необходимо одновременно решать (N-2)*(N-2) линейных алгебраических уравнений с (N-2)*(N-2) неизвестными.
В данной лабораторной работе используется итерационный метод Гаусса-Зайделя, который при применении к уравнению Лапласа часто, как уже отмечалось, называют методом Либмана (ω=1). Для ускорения сходимости данного итерационного процесса используется метод последовательной верхней релаксации с ускоряющим множителем ω, причем 
. При ω=1 реализуется сам метод Гаусса-Зайделя без ускорения, а при 
- метод последовательной нижней релаксации, замедляющий процесс сходимости.
Как отмечалось, в данной лабораторной работе используется также метод последовательной верхней релаксации с ускоряющим множителем ω, причем 1< ω <2. Этот метод может быть использован для ускорения любого итерационного процесса (в данной лабораторной работе - метода Гаусса-Зайделя). Идея его состоит в коррекции неизвестных на очередном шаге итерации
, где
- скорректированное значение неизвестной на новом (n+1) шаге итерации;
- значение неизвестной на последнем (n+1) шаге итерации (без коррекции);
- значение неизвестной на предыдущем n шаге итерации.