Методы решения уравнения Лапласа, использующие идею принципа установления

В данной лабораторной работе предлагается использовать для решения эллиптического уравнения Лапласа конечно-разностные методы, основанные на принципе установления.

Принцип установления заключается в том, что стационарное решение эллиптической задачи находится как предел нестационарного решения соответствующей маршевой задачи при стремлении к бесконечности времени процесса (т.е. при ). Естественно, что все граничные условия новой маршевой задачи должны быть стационарными (т.е. не зависящими от времени) и такими же, что и у исходной эллиптической.

В приложении к рассматриваемому в данной лабораторной работе уравнению Лапласа принцип установления выглядит следующим образом:

необходимо найти решение уравнения Лапласа (3) с граничными условиями (4) как предел решения нестационарного двумерного уравнения «теплопроводности» параболического типа (7) с граничными условиями (8) при стремлении к бесконечности времени процесса (т.е. при ).

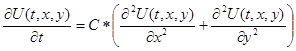(7)

U(t,x,y) │ = f(x,y), (8)

│ s

C - коэффициент «температуропроводности». Причем физический смысл этот коэффициент «С» имеет лишь в случае, когда интерес представляет решение собственно уравнения теплопроводности (7). Если же (как в данной лабораторной работе) необходимо получить только стационарное решение эллиптического уравнения (3), коэффициент «С» не имеет физического смысла и выбирается из других соображение (например, для улучшения свойств применяемой конечно-разностной схемы).

Для решения параболической задачи (7) требуется (чтобы задача была корректно поставлена) знание начальных условий при t=0, т.е.

U(0,x,y)=g(x,y) (9),

которые необходимо задавать точно только в случае, когда исследователя интересуют нестационарные решения собственно уравнения (7). Если же решается уравнение (3), т.е. представляет интерес только стационарное решение, то выбор начальных условий достаточно произволен. Хотя и он должен удовлетворять определенным требованиям. Естественно, чем ближе будут выбраны начальные условия g(x,y) к искомому решению эллиптического уравнения (3), тем быстрее (и с меньшими трудностями) будет получено само это решение.

Таким образом, эллиптическая задача (3, 4) сводится к решению параболической задачи (7, 8, 9). И в дальнейшем рассматриваются конечно-разностные методы решения именно параболической задачи – уравнения теплопроводности (7) с граничными условиями (8) и начальными условиями (9).

Необходимо отметить, что если исследователя интересует только стационарное решение эллиптической задачи, то ему неважна точность промежуточных решений (решений, полученных при текущем значении времени t) параболического уравнения. Важен только конечный результат, т.е. решение, полученное при 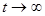. При этом, это «установившееся» решение не будет зависеть ни от выбора коэффициента «С », ни, как отмечалось, от выбора начальных данных U(0,x,y)=g(x,y).

№ п/п	Наименование метода	Явный / неявный	Порядок аппрокси-мации	Согласо-ванность	Устой-чивость	Сходи-мость	Ошибки	Кол. шагов (проходов)
	Схема Рунге	---	второй	абсолютная	---	абсолютная	только диссипативные	однощаг.
	Простой явный метод	явный	второй (для стац. решения)	абсолютная		услов	только диссипативные	одношаг.

Содержание работы

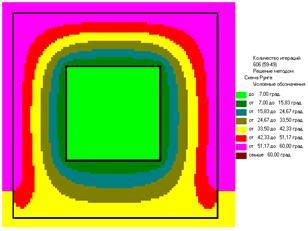
3.4.1. Моделируются стационарные поля температур в квадратной трубе (со стороной A), имеющей квадратное отверстие (со стороной B), по которой течет нагретая жидкость с неизменной температурой T₁. Сама труба частично опущена (на высоту H₀) в ванну с постоянной температурой T₂. Верхняя часть трубы находится при температуре T₃. См. рисунок.

Труба считается достаточно длинной, внешние условия - неизменными. Это позволяет рассматривать плоскую задачу. Распределение температур при этом удовлетворяет уравнению Лапласа (3) со следующими граничными условиями:

T(0,x)=T₂; T(A,x)=T₃ при 0 ≤ x ≤ A

T(y,0)=T(y,A)=T₂ при 0 ≤ y ≤ H₀;

T(y,0)=T(y,A)=T₃ при H₀ < y ≤ A;