Давление в конце впуска [1]:
(1.12)
где,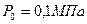 
– атмосферное давление;
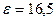– степень сжатия;
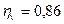– коэффициент наполнения;
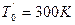– температура подогретого заряда;
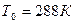– температура окружающей среды.
Определяем давление и температуру остаточных газов:
(1.13)
Они будут равны:
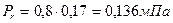
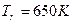
Тогда:
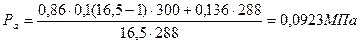
Коэффициент остаточных газов:
Принимаем температуру подогрева свежего заряда 
.
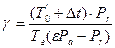, (1.14)
где: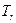 
– температура остаточных газов.
Тогда
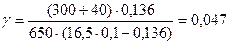
Температура в конце впуска определяем по формуле:
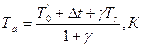(1.15)
Расчет параметров сжатия
Значение показателя политропа сжатия можно определить по формуле [1]:
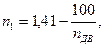(1.16)
где: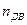 
– число оборотов двигателя.
Тогда получаем:
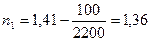
Считая процесс сжатия политропным, можно рассчитать температуру и давление в конце процесса сжатия.
Давление в конце сжатия:
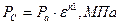(1.17)
Тогда давление будет:
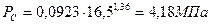
Температура в конце сжатия:
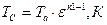(1.18)
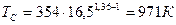
Число молей остаточных газов определяем по формуле:
(1.19)
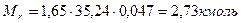
Число молей в конце процесса сжатия:
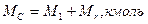(1.20)
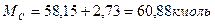
Средняя молярная теплоемкость свежего заряда:
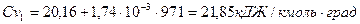
Расчет параметров сгорания
Определяем число молей газов после сгорания [1]:
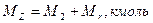(1.21)
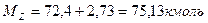
Коэффициент молекулярного изменения смеси определяем по формуле:
(1.22)
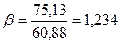
Средняя молярная теплоемкость при постоянном объеме определяется
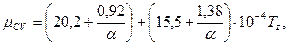(1.23)
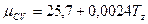
Запишем уравнение сгорания:
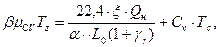(1.24)
где: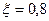 
коэффициент использования тепла.
При подстановке в уравнение значений получаем квадратное уравнение:
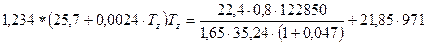
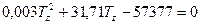
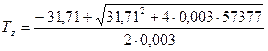
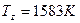
Давление в конце сгорания определяют по формуле:
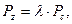(1.25)
где: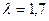 
– степень повышения давления.
Тогда получим:
Степень предварительного расширения определяется как:
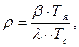(1.26)
Определяем степень последующего расширения:
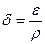(1.27)
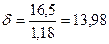
Расчет параметров расширения
Давление в конце процесса расширения определяем по формуле [1]:
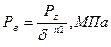, (1.28)
где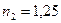 
– показатель политропного расширения.
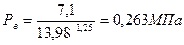
Температура в конце расширения:
, (1.29)
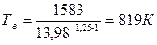
Выполним проверку ранее принятой температуры остаточных газов:
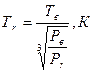(1.30)
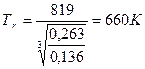
Ошибка составляет:
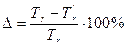, %, (1.31)
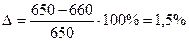
Расчет верен, так как ошибка не превышает оптимальной величины 
Показатели рабочего цикла двигателя
Теоретическое среднее индикаторное давление определяется по формуле [5]:
(1.32)
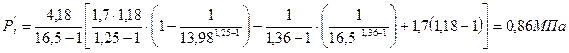
Действительное индикаторное давление будет равно:
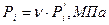(1.33)
где: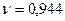 
– коэффициент диаграммы (рис. 1.1).
Получаем:
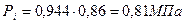
Среднее эффективное давление:
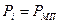
где: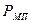 
– давление механических потерь.
Давление механических потерь определяется по формуле:
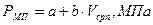(1.34)
где: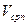 
– средняя скорость поршня.
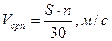(1.35)
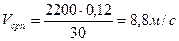
Тогда давление механических потерь будет равно:
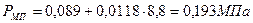
Определяем среднее эффективное давление:
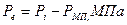(1.36)
Тогда среднее эффективное давление будет равно:
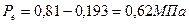
Исходя из этого, определим мощность двигателя:
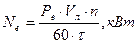(1.37)
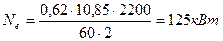
Механический коэффициент полезного действия:
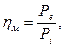(1.38)
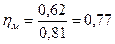
Результаты расчета сводим в таблицу 1.1.
Таблица 1.1 – Параметры цикла двигателя
| Процесс | Параметры | |
| Температура, К | Давление, МПа | |
| Впуск | 0,0923 | |
| Сжатие | 4,18 | |
| Сгорание | 7,1 | |
| Расширение | 0,263 |
Динамический расчет двигателя
Построение диаграмм перемещения, скорости и ускорения
Расчет производим по выражениям [5]:
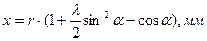(1.39)
(1.40)
(1.41)
где: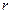 
– радиус кривошипа, мм;
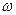– угловая скорость, рад/с;
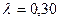– коэффициент.
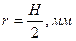(1.42)
где: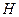 
- ход поршня.
Данные расчета заносим в таблицу 1.2.
Таблица 1.2 – Расчет перемещения скорости и ускорения (рис. 1.1)
| a0 | |||||||||||||
| х, мм | 0,0102 | 0,0363 | 0,0684 | 0,0963 | 0,114 | 0,12 | 0,114 | 0,0963 | 0,0684 | 0,0363 | 0,0102 | ||
| V, м/с | 8,693 | 13,744 | 13,800 | 10,158 | 5,107 | -5,107 | -10,158 | -13,800 | -13,744 | -8,693 | |||
| j×103 м/с2 | 3,650 | 2,987 | 1,350 | -0,476 | -1,825 | -2,511 | -2,698 | -2,511 | -1,825 | -0,476 | 1,350 | 2,987 | 3,650 |