Векторы на плоскости
| Вектором называется отрезок, у которого указаны начало и конец (т.е. величина, которая характеризуется численным значением и направлением). | 
|
Координаты и длина вектора
Даны точки А(х1;у1) и В(х2; у2)
Координаты вектора
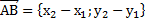
| 
|
Длина вектора 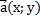 вычисляется по формуле: вычисляется по формуле:
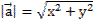
| |
| Координаты вектора не изменяются при параллельном переносе. | |
Действия над векторами
Если  , то , то


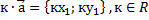
| 
|
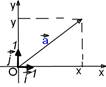
Разложение вектора по координатным векторам
Если 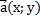 , то , то 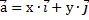
| 
|
Коллинеарные векторы
Коллинеарными называются векторы, лежащие на одной прямой или на параллельных прямых.
Условие коллинеарности векторов  в координатном представлении: в координатном представлении:
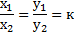
| 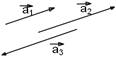
 - сонаправленные векторы - сонаправленные векторы
 - противоположно направленные векторы - противоположно направленные векторы
|
Равные векторы
 ,если: ,если: 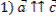
 У равных векторов соответствующие координаты равны.
Противоположные векторы (
У равных векторов соответствующие координаты равны.
Противоположные векторы ( 
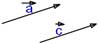
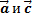 противоположные векторы,если:
1) противоположные векторы,если:
1)  2)
2)  Соответствующие координаты противоположны.
Соответствующие координаты противоположны.
|
|
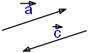
Ортогональные векторы
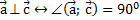 Условие ортогональности (перпендикулярности) векторов,
Условие ортогональности (перпендикулярности) векторов,  на плоскости: на плоскости:
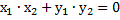
| 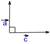
 - ортогональные векторы - ортогональные векторы
|
Скалярное умножение векторов
Скалярным произведением двух векторов 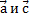 называется число, равное произведению длин этих векторов на косинус угла j между ними: называется число, равное произведению длин этих векторов на косинус угла j между ними:
 Скалярное произведение векторов
Скалярное произведение векторов 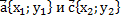 выражается через координаты: выражается через координаты:

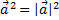 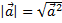
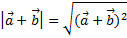

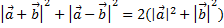
| 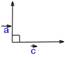 j=900 ® j=900 ® 
 00≤j<900 ® 00≤j<900 ® 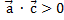
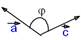 900<j≤1800 ® 900<j≤1800 ® 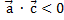
|
Применение скалярного произведения к решению задач
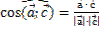 
|
Метод координат в пространстве
| Прямые x,y,z называются координатными осями (или осями координат), Оси координат обозначаются так: OX- ось абсцисс OY- ось ординат OZ- ось аппликат точка их пересечения O – началом координат, а плоскости xOy, xOz и yOz – координатными плоскостями. В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел, которые называются ее координатами. М(x; y; z). |
Прямоугольная система координат в пространстве
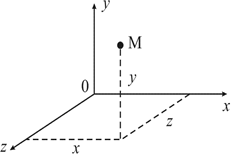
|
| Действия над векторами: |
Сложение векторов

|
Вычитание векторов

|
Умножение вектора на число k.

|
Координаты середины отрезка AB:
А(x1;y1;z1), B(x2;y2;z2).
Точка М середина отрезка AB.

|
Вычисление длины вектора  по его координатам: по его координатам:
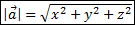
|
Расстояние между двумя точками.
А(x1;y1;z1) и B(x2;y2;z2).

|
Вычисление координат вектора 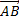 . Если А(x1;y1;z1), B(x2;y2;z2). . Если А(x1;y1;z1), B(x2;y2;z2).

|
Скалярное произведение векторов  и и  выражается формулой: выражается формулой:
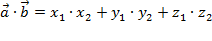
|
Перпендикулярность векторов:  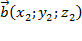 ; ;

|
Коллинеарность векторов:  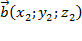 ; ;
 ,если координаты векторов не равны нулю. ,если координаты векторов не равны нулю.
|
Косинус угла между ненулевыми векторами векторов  и и  вычисляется по формуле: вычисляется по формуле:

|
Задачи по теме «векторы в пространстве»
1. Даны координаты точек А(-3; 2; -1), В(2; -1;-3), С(1; -4; 3), Д(-1; 2; -2).
Найдите | 2АВ+3СД |
Решение:
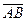 (2+3; -1-2;-3+1)=(5;-3;-2)
(2+3; -1-2;-3+1)=(5;-3;-2)
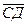 (-1-1;2+4;-2-3)=(-2;6;-5).
(-1-1;2+4;-2-3)=(-2;6;-5).
2 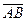 +3
+3 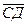 =(10+(-6);-6+18;-4-15)=(4;12;-19).
=(10+(-6);-6+18;-4-15)=(4;12;-19).

 +3
+3 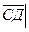 =
=  =
= 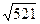
Ответ: 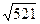
2. Даны координаты точек С(3; -2; 1), Д(-1; 2; 1), М(2; -3;3), N(-1; 1; -2). Найдите косинус угла между векторами 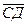 и
и  .
.
Ответ:0,7
3. Вычислите угол между векторами  (2; -2; 0) и
(2; -2; 0) и  (3; 0; -3).
(3; 0; -3).
Ответ:600
4. При каком значении n данные векторы перпендикулярны:  (2; -1;3) и
(2; -1;3) и  (1;3; n)?
(1;3; n)?
Ответ: 
5. Вычислите координаты вектора 2  +3
+3  +
+  по координатам векторов:
по координатам векторов:  (3;1; 1),
(3;1; 1),  (-2;0;2)
(-2;0;2)
Ответ:(1;1;8)
6. Вычислите значение k, при котором скалярное произведение векторов  (2;k;-1) и
(2;k;-1) и
Ответ: 
7. Даны векторы:  (-3;-1;2),
(-3;-1;2),  (5;-2;7). Найдите координаты вектора: -
(5;-2;7). Найдите координаты вектора: -  +3
+3  .
.
Ответ:(18;-5;-19)
8. При каких значениях x и у векторы а(х;-2;5) и b(1;у;-3) коллинеарные?
Ответ:x= 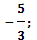
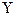 =
= 
9. Вычислите длину вектора 2  + 3
+ 3  , если
, если  (3; 1;0),
(3; 1;0),  (0;1;-1).
(0;1;-1).
Ответ:

10. Даны две точки А(2;-1;3), В(1;0;4) и вектор  (4;-2;-3). Найдите длину вектора 3
(4;-2;-3). Найдите длину вектора 3 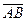 + 5
+ 5 
Ответ: 
11. Даны точки А(2;0;1), В(4;-1;3), С(1;1;2). Найдите косинус внутреннего угла при вершине В треугольника АВС.
Ответ: 
12. Найдите сумму всех значений m, при которых векторы а(m + 1; 1;-1;) и b(m; -m;-2m+3) перпендикулярны.
Ответ:-2
13. Найдите длину большей диагонали параллелограмма, построенного на векторах  (3;-3;-2) и
(3;-3;-2) и  (1;2;-1).
(1;2;-1).
Ответ: 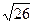
14. Найдите в градусах угол между векторами  (1;1;
(1;1;  ) и осью Оz.
) и осью Оz.
Ответ: 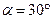
15. Даны векторы  (-1;1;1;)
(-1;1;1;)  (0;2;-2). Найдите координаты вектора с
(0;2;-2). Найдите координаты вектора с  =(2
=(2  +3
+3  )-(
)-( -2)
-2)  +2(
+2( -
-  ).
).
Ответ:  (-3;9;-3)
(-3;9;-3)
16. Найдите значения m и n, при которых следующие векторы коллинеарные:  (15;m;1) и
(15;m;1) и  (18;12;n)
(18;12;n)
Ответ:m=10,n=1,2
17. Даны векторы  =mi+3j+4k и
=mi+3j+4k и  =(4i+mj-7k). При каком значении векторы ортогональны?
=(4i+mj-7k). При каком значении векторы ортогональны?
Ответ:4
18. Даны векторы  (-1;2;3) и
(-1;2;3) и  (5;х;-1). При каком значении х выполняется условие аb=3?
(5;х;-1). При каком значении х выполняется условие аb=3?
Ответ:5,5
19. Вершины треугольника АВС имеют координаты А(-2;0;1), В(-1;2;3) и С(8;-4;9). Найдите координаты вектора ВМ, если ВМ медиана треугольника АВС.
Ответ:  (4;-4;2)
(4;-4;2)
20. Даны вершины треугольника: А(-1;-2;4), В(-4;-2;0) и С(3;-2;1). Найдите угол треугольника при вершине А.
Ответ: 
21. Вычислите 
 +
+  c+
c+  c, если,
c, если,  +b+c=0 и |
+b+c=0 и |  |=|
|=|  |=|c|=1.
|=|c|=1.
Ответ:-1,5
22. Вычислите длину вектора  =2i+j-3k.
=2i+j-3k.
Ответ: 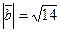
23. Найдите косинус угла между векторами  -
-  и
и  +
+  , если
, если  (1;2;1) и
(1;2;1) и  (2;-1;0).
(2;-1;0).
Ответ:cos 

24. Найдите скалярное произведение векторов  и
и  , если |
, если |  |=1, |
|=1, |  |=2, |a+b|=3.
|=2, |a+b|=3.
Ответ:2
25. Найдите угол между векторами р=2  +3
+3  и q=2
и q=2  -3
-3  , если
, если  =i-j+2kи
=i-j+2kи  =2i+2j
=2i+2j
Ответ:cos  =
= 
26. В параллелограмме АВСД заданы АВ(-4;-4;-2), СВ(-3;-6;1) и А(3;8;-5). Найдите сумму координат точки пересечения диагоналей.
Ответ:5
27. Длина вектора  (х;у;z) равна 5. Найдите ординату вектора
(х;у;z) равна 5. Найдите ординату вектора  , если х=2, z=-
, если х=2, z=- 
Ответ:  4
4
28. Даны три точки А(1;0;1), В(-1;1;2) и С(0;2;-1). Найдите точку Д(х;у;z), если векторы АВ и СД равны.
Ответ:Д(-2;3;0)
29. При каком значении (значениях) k векторы  (6-k;k;2) и
(6-k;k;2) и  (-3;5+5k;-9) перпендикулярны?
(-3;5+5k;-9) перпендикулярны?
Решение:
 =0
=0
-3(6-k)+k(5+5k)-18=0
-18+3k+5k+5k 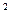 -18=0
-18=0
5k 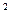 +8k-36=0
+8k-36=0
(+)=-8
(*)=-180
k 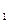 =
=  =2 k
=2 k  =-
=- 
Ответ:k 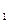 =2, k
=2, k  =
= 
30. При каком значении а векторы АВ и СД коллинеарны, если А(-2;-1;2), В(4;-3;6),
С(-1;а-1;а), Д(-4;-1;а)?
Ответ:-1
31. Дано: |  |=4, |
|=4, |  |=1.
|=1.  . Найдите cosa, где а – угол между векторами
. Найдите cosa, где а – угол между векторами  -
-  и
и 
Ответ:cos 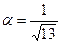
32. Найдите длину вектора a+b+c, если |a|=1 |b|=2, |c|=3,.  ,
,  .
.
Ответ: 
33. В параллелограмме АВСД заданы СД(-3;4;2), СИ(5;-2;4) и А(5;8;0). Найдите расстояние от точки С до начала координат.
Ответ: 
34. Точки А(14;-8;-1), В(7;3;-1), С(-6;4;-1), Д(1;-7;-1) являются вершинами ромба АВСД. Найдите острый угол ромба 
Ответ: 
35. Дан треугольник с вершинами в точках А(3;-2;1), В(3;0;2), С(1;2;5). Найдите угол, образованный медианой ВД и основанием АС.
Ответ: 
36. В правильном тетраэдре ДАВС с ребром а точка О – центр треугольника АВС. Найдите | 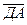 +
+ 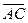 -
- 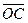 |.
|.
Ответ: 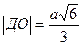
37. Даны три точки: А(1;0;10, В(-1;1;2), С(0;2;-1). Найдите на оси Оz такую точку Д(0;0;с), чтобы векторы 
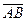 и
и 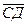 были перпендикулярны.
были перпендикулярны.
Ответ:1
38. В тетраэдре ДАВС ДА=ДВ=ДС, 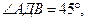
 . Вычислите угол между векторами: а)
. Вычислите угол между векторами: а) 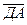 и
и 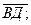 б)
б) 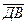 и
и 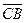 .
.
Ответ:600 ; 1350
39. При каком значении а три точки А(2;а; 3), В(3;1;6), С(4;3;9) лежат на одной прямой?
Ответ:-1
40. Найдите длину интервала значений параметра а, при которых р(-1;2х;х 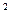 ) и q(5;а;а) при любом х образуют тупой угол.
) и q(5;а;а) при любом х образуют тупой угол.
Ответ:5
41. Найдите длину вектора  -
-  -
-  ,если |
,если |  |=2, |
|=2, |  |=3,|
|=3,|  |=4, угол между
|=4, угол между  и
и  равен
равен  , между
, между  и
и  равен
равен  и между
и между  и
и  равен
равен  .
.
Ответ: 
42. Векторы  и
и  взаимно перпендикулярны, вектор
взаимно перпендикулярны, вектор  образует с ними угол
образует с ними угол 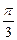 . Зная, что
. Зная, что 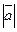 =3,
=3,  =5,
=5, 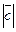 =8, вычислите скалярное произведение
=8, вычислите скалярное произведение 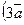 -
- 
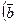 +
+ 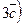 .
.
Ответ:-62
43. Треугольная пирамида задана координатами своих вершин А(3;0;1), В(-1;4;1), С(5;2;3) и Д(0;-5;4). Вычислите длину вектора 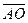 , если О – точка пересечения медиан треугольника ВСД.
, если О – точка пересечения медиан треугольника ВСД.
Ответ: 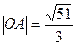
44. 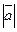 =2,
=2,  =3,
=3,  ,
,  )=120. Найдите cos
)=120. Найдите cos  , где
, где  - угол между векторами
- угол между векторами  и
и  +
+  .
.
Ответ:cos 
45. Треугольник задан координатами своих вершин А(1;1;2), В(3;4;2) и С(5;6;4). Найдите величину внешнего угла треугольника при вершине В.
Ответ: 
46. В треугольнике АВС точки M и N – середины сторон АВ и ВС соответственно. Известно, что 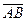 (3;-5;6),
(3;-5;6),  (-2;1;7). Найдите сумму координат вектора
(-2;1;7). Найдите сумму координат вектора  .
.
Ответ:8
47. Найдите сумму целых значений параметра b, при которых векторы  (х
(х 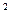 ;х; 16) и
;х; 16) и
 (1;b;-
(1;b;- 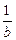 )
)  при всех значениях х образуют острый угол.
при всех значениях х образуют острый угол.
Ответ:-6
48. В пространстве расположены три точки, заданные своими координатами: A(1; 6; 3), B (3; − 1; 7) и C(− 4; 3; − 2). Найти координаты векторов 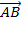 ,
,  и
и  .
.
Ответ:  ;
; 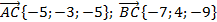
49. Вычислить скалярное произведение векторов 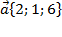 и
и 
Ответ:12
50. Коллинеарны ли векторы?:
a)  {-5;3;-1} и
{-5;3;-1} и  {-10; 6;-2};
{-10; 6;-2};
b) 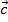 {-6;3;-1} и
{-6;3;-1} и  {2; -9;3};
{2; -9;3};
Ответ: a) да b) нет
51. Найти косинус угла между векторами  = {4; 3; 0} и
= {4; 3; 0} и  = {0; 12; 5}.
= {0; 12; 5}.
Ответ:36/65