Практика 20. 1-й, 2-й замеч. пределы и их следствия.
«1-й замечательный предел».
Задача 197. Найти предел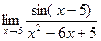 
.
Решение. С помощью преобразований получим в знаменателе такое же выражение, как под знаком синуса в числителе.
= 
= 
= 
= 
.
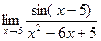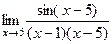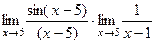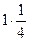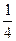Второй предел вообще не содержит неопределённости, а первый это в точности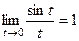 
если переобозначить 
.
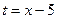Ответ. .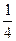
Задача 198. Найти предел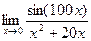 
.
Решение. =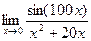 
= 
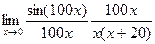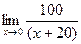= 5.
Ответ. 5.
Задача 199. Найти предел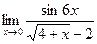 
.
Решение. =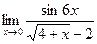 
=
= 
=
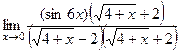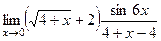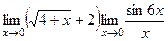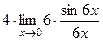= 24.
Сначала домножили на сопряжённое выражение, потом вынесли в отдельный множитель ту часть, где нет неопределённости. В конце домножили на 6 в знаменателе и числителе, чтобы в знаменателе образовалось ровно такое же выражение, как под знаком синуса, то есть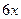 
.
Ответ. 24.
Задача 200. Найти предел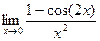 
.
Решение. Эту задачу можно решить как с применением тригонометрической формулы, так и методом Лопиталя.
Способ 1. По формуле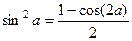 
. Получается
= 
= 
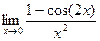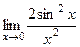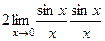= 2.
Способ 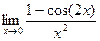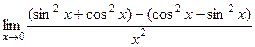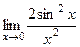2. = 
= = 2.
Ответ. 2.
Задача 201. Найти предел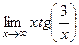 
.
Решение. =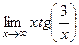 
= 
=
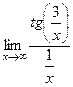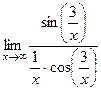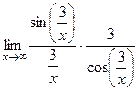= (замена 
) 
=
= 
.
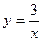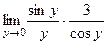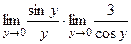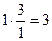Ответ. 3.
«2-й замечательный предел».
Задача 202. Найти предел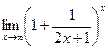 
.
Решение. Здесь целая часть 1 выделена в явном виде. Остаётся только домножить и найти предел в степени.
= 
=
= 
= 
= 
= 
= 
.
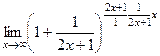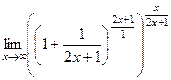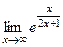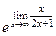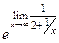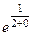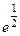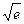Ответ. .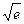
Задача 203. Найти предел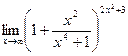 
.
Решение.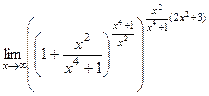 
= 
=
= 
= 
= 
.
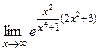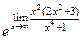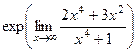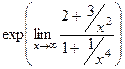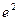Ответ. .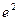
Задача 204. Найти предел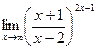 
.
Решение. Здесь неопределённость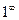 
. Основание стремится к 1, так как здесь одинаковые старшие степени многочленов в числителе и знаменателе, и одинаковые коэффициенты при них. Отделим от дроби её целую часть, то есть 1.
= 
= 
= 
.
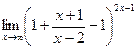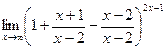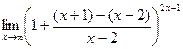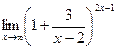Слагаемое, которое следует после 1, стремится к 0, что и должно быть для 2 замечательного предела. Далее,
= 
=
= 
= 
= 
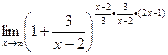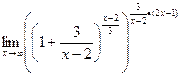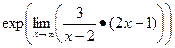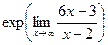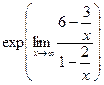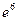. Ответ. 
.
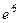Задача 205. Найти предел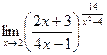 
.
Решение. Здесь сначала заметим, что основание стремится к 7/7 = 1. А степень к бесконечности. То есть, неопределённость типа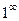 
и можно использовать 2-й замечательный предел. Сначала выделяем целую часть дроби, то есть 1. Прибавим и отнимем 1, но ту, которую отняли, представим в таком виде, чтобы она объединилась с дробью.
= 
= 
=
= 
= 
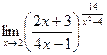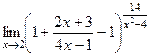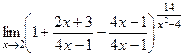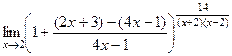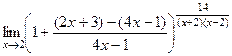
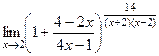теперь после 1 следует бесокнечно-малая, которая обращается в 0 при 
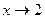, ведь там числитель 
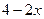. Далее, в степени домножаем обратную к этой дроби, но при этом и её саму тоже, чтобы ничего не изменилось.
= 
= 
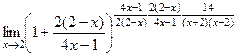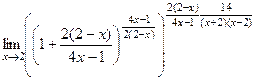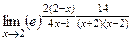
использовали тот факт, что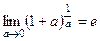 
.
Далее, получаем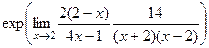 
=
= 
= 
.
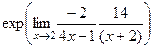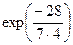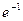Ответ. .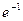
Задача 206. Найти предел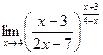 
.
Решение. Заметим, что основание стремится к 1, неопределённость типа 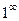, можно использовать 2-й замечательный предел.
= 
= 
=
= 
= 
= 
=
= 
= 
.
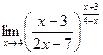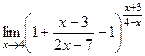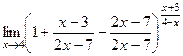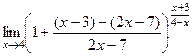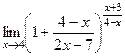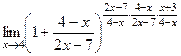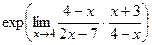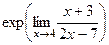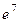Ответ.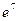 
.
Задача 207. Найти предел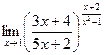 
.
Решение. =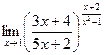 
= 
= 
=
= 
=
= 
= 
.
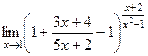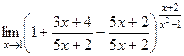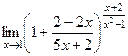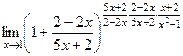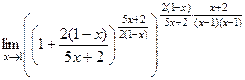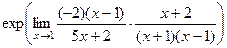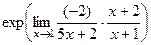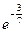Ответ. .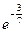
Замечание. Некоторые особенности вычислений, в которых не требуется второй замечательный предел. Если основание стремится не к 1, а к числу a<1 а степень к бесконечности, то можно сразу сделать вывод, что предел 0. Если a>1 то наоборот,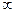 
.
, 
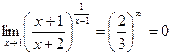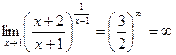
Если основание и показатель стремятся к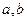 
соответственно, то 2-й зам. предел не требуется, а ответ 
.
.
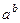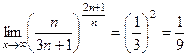Задачи со следствиями из 1 и 2 зам. пределов.
Задача 208. Найти предел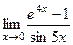 
.
Решение. Применяя эквивалентность бесконечно-малых,
= 
= 
= 
.
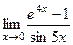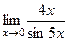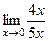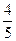Ответ. .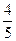
Задача 209. Найти предел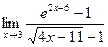 
.
Решение.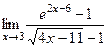 
= 
=
= 
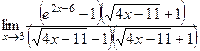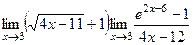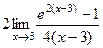. Введём замену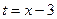 
Тогда 
= 
= 
= 
.
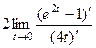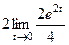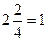Ответ. 1.
Замечание. Почему выражение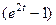 
мы здесь не домножаем на сопряжённое, а делали методом Лопиталя. Тогда получилось бы 
= 
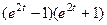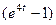, то есть в таких выражениях, в отличие от иррациональностей, формулу сокращённого умножения и структуру 
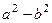применять бесполезно, потому что это даёт точно такое же выражение, стремящееся к 
.
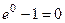Задача 210. Найти предел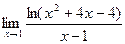 
Решение. Способ 1. С помощью замены на эквивалентную бесконечно-малую. Можно выделить 1 под знаком логарифма, получить выражение типа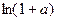 
. Затем воспользоваться эквивалентностью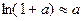 
= 
= 
=
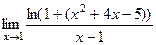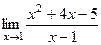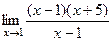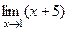= 6.
Способ 2. По правилу Лопиталя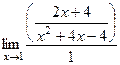 
= 
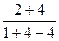= 6.
Ответ. 6.