МАГНИТНОЕ ПОЛЕ ПОСТОЯННОГО ТОКА

Уважаемые студенты, высылаю вам примеры решения задач по различным темам курса физики (II семестр). Вам необходимо изучить и постараться разобраться в этих примерах. Это поможет вам успешно выполнить лабораторные работы. Лабораторные работы вы получите на занятии по расписанию. Там же будет подробная инструкция по выполнению и оформлению лабораторной работы.

ВНИМАНИЕ! Каждый студент после получения каждой лекции, практического задания или лабораторного задания должен отправить мне на почту сообщение следующего содержания:

Я Ф.И.О., студент группы …. (например20ПИз.о,20ЭТз.о, и т.д.) материал для изучения (физики) получил.

Это будет своего рода перекличкой, т.е. свидетельство вашего присутствия на сессии.

 

ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

ОСНОВНЫЕ ЗАКОНЫПОСТОЯННОГО ТОКА

Основные формулы

· Сила постоянного тока

I=Q/t,

где Q - количество электричества, прошедшее сечение проводника за время t.

· Плотность электрического тока есть векторная величина, равная отношению силы тока к площади S поперечного сечения проводника:

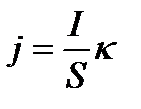
где 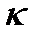- единичный вектор, по направлению совпадающий с правлением движения положительных носителей заряда.

· Сопротивление однородного проводника

R=ρl/S,

где ρ - удельное сопротивление вещества проводника; l - его длина.

· Проводимость G проводника и удельная проводимость γ вещества

G= 1 /R, γ =l/ρ.

· Зависимость удельного сопротивления от температуры

ρ =ρ ₀(1 +αt),

где ρ и ρ₀ - удельные сопротивления соответственно при t и 0 ˚С; t -температура (по шкале Цельсия); α- температурный коэффи­циент сопротивления.

· Сопротивление соединения проводников:

последовательного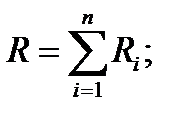

параллельного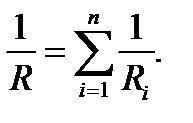

Здесь Ri - сопротивление i- гопроводника; п - число провод­ников.

· Закон Ома:

для неоднородного участка цепи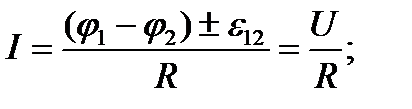

для однородного участка цепи ;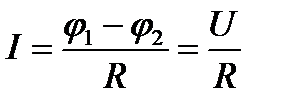

для замкнутой цепи .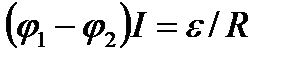

Здесь (φ₁-φ₂) - разность потенциалов на концах участка цепи; ε ₁₂ - ЭДС источников тока, входящих в участок; U - напряжение на участке цепи; R - сопротивление цепи (участка цепи); ε - ­ЭДС всех источников тока цепи.

· Правила Кирхгофа. Первое правило: алгебраическая сумма сил токов, сходящихся в узле, равна нулю, т. е.

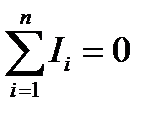
где n - число токов, сходящихся в узле.

Второе правило: в замкнутом контуре алгебраическая сумма на­пряжений на всех участках контура равна алгебраической сумме электродвижущих сил, т.е.

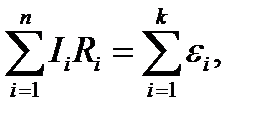
где I _i - сила тока на i- мучастке; R _i - активное сопротивление на i- мучастке; ε_i- ЭДС источников тока на i- мучастке; п - ­ число участков, содержащих активное сопротивление; k- число участков, содержащих источники тока.

· Работа, совершаемая электростатическим полем и сторонними силами в участке цепи постоянного тока за время t,

A=IUt;

· Мощность тока

P=IU.

· Закон Джоуля - Ленца

Q=I ² Rt,

где Q - количество теплоты, выделяющееся в участке цепи за время t;

Закон Джоуля - Ленца справедлив при условии, что участок цепи неподвижен и в нем не совершаются химические превращения.

Примеры решения задач

Пример 1. Определить заряд Q, прошедший по проводу с сопро­тивлением R= 3Ом при равномерном нарастании напряжения на концах провода от U ₀ = 2В до U = 4В в течение t= 20с.

Р е ш е н и е. Так как сила тока в проводе изменяется, то вос­пользоваться для подсчета заряда формулой Q=It нельзя. Поэтому возьмем дифференциал заряда d Q=I d t и проинтегрируем:

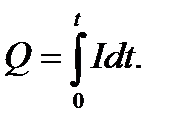(1)

Выразив силу тока по закону Ома, получим

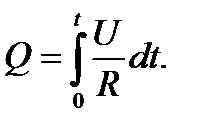(2)

Напряжение U в данном случае переменное. В силу равномерности нарастания оно может быть выражено формулой

U= U ₀ +kt, (3)

где k - коэффициент пропорциональности. Подставив это выражение U в формулу (2), найдем

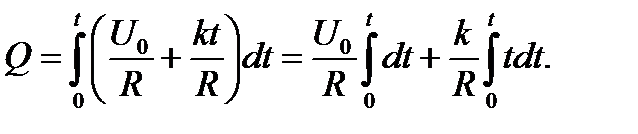
Проинтегрировав, получим

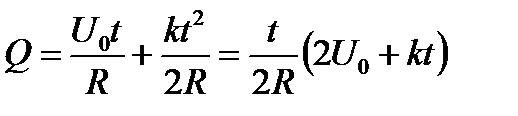(4)

Значение коэффициента пропорциональности k найдем из формулы (3), если заметим, что при t= 20 с U= 4В:

k= (U-U ₀) /t= 0,1B/c.

Подставив значения величин вформулу (4), найдем

Q= 20Кл.

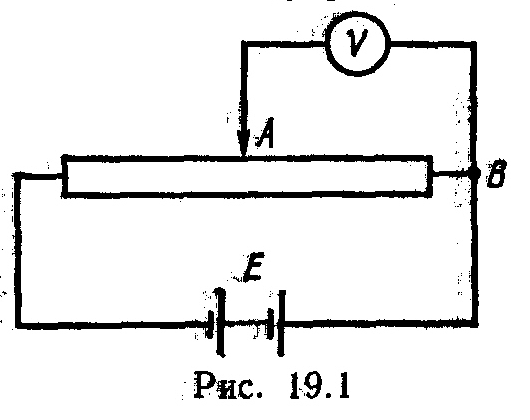П р и м е р 2. Потенциометр с сопротивлением R = 100Ом подклю­чен к источнику тока, ЭДС ε которого равна 150 В и внутреннее со­противление r = 50 Ом (рис. 19.1). Определить показание вольтметра с сопротивлением R _B = 500Ом, соединенного проводником с одной из клемм потен­циометра и подвижным контактом с се­рединой обмотки потенциометра. Какова разность потенциалов между теми же точками потенциометра при отключен­ном вольтметре?

Р е ш е н и е. Показание U ₁ вольт­метра, подключенного к точкам А и В (рис. 19.1), определяется по формуле

U ₁ =I ₁ R ₁, (1)

где I ₁ - сила тока в неразветвленной, части цепи; R ₁- сопротивление параллельно соединенных вольтметра и половины потенциометра.

Силу тока I ₁ найдем по закону Ома для всей цепи:

I ₁ = ε/(R+r), (2)

где R - сопротивление внешней цепи.

Внешнее сопротивление R есть сумма двух сопротивлений:

R=R/2+R₁. (3)

Сопротивление R ₁параллельного соединения может быть най­дено по формуле 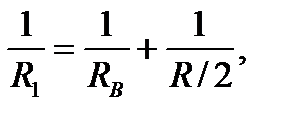откуда

R _l= RR _B /(R + 2 R _B).

Подставив в эту формулу числовые значения величин и произве­дя вычисления, найдем

R _l=45,5Ом.

Подставив в выражение (2) правую часть равенства (3), опреде­лим силу тока:

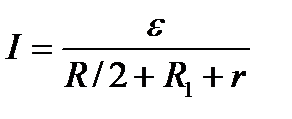=1,03 А

Если подставить значения I ₁ и R ₁в формулу (1), то найдем пока­зание вольтметра: U ₁ = 46,9В.

Разность потенциалов между точками А и В при отключенном вольтметре равна произведению силы тока I ₂ на половину сопротивления потенциометра, т. е. U ₂ =I ₂ (R/ ₂), или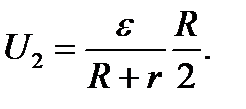

Подставив сюда значения величин ε, r и R получим

U ₂ = 50В.

Пример 3. Источники тока с электродвижущими силами ε ₁и ε ₂включены в цепь, как показано на рис. 19.2. Определить силы токов, текущих в сопротивлениях R ₂ и R ₃, если ε ₁ = 10 В иε₂ = 4В, а R ₁ =R ₄ = 20ми R ₂ =R ₃ = 4Ом. Сопротивлениями источников тока пренебречь.

Р е ш е н и е. Силы токов в разветвленной цепи определяют с помощью законов Кирхгофа. Чтобы найти четыре значения силы токов, следует составить четыре уравнения.

 

Указание. Перед составлением уравнений по закону Кирхгофа необхо­димо, во-первых, выбрать произвольно направления токов, текущих через сопротивления, указав их стрелками на чертеже, и, во-вторых, выбрать на­правление обхода контуров (последнее только для составления уравнений по второму закону Кирхгофа).

 

Выберем направления токов, как они показаны на рис. 19.2, и условимся обходить контуры по часовой стрелке.

Рассматриваемая в задаче схема имеет два узла: А и В. Но состав­лять уравнение по первому закону Кирхгофа следует только для одного узла, так как уравнение, составленное для второго узла, будет следствием первого уравнения.

При составлении уравнений по первому закону Кирхгофа необ­ходимо соблюдать правило знаков: ток, подходящий к узлу, входит в уравнение со знаком плюс; ток, отходящий от узла, - со знаком минус.

По первому закону Кирхгофа для узла В имеем

I ₁+ I ₂+ I ₃- I ₄=0.

Недостающие три уравнения получим по второму закону Кирхгофа. Число независимых уравнений, которые могут быть составле­ны по второму закону Кирхгофа, также меньше числа контуров (в нашем случае контуров шесть, а независимых уравнений три). Чтобы найти необходимое число независимых уравнений, следует придерживаться правила: выбирать контуры таким образом, чтобы в каждый новый контур входила хотя бы одна ветвь, не участвовав­шая ни в одном из ранее использованных контуров.

При составлении уравнений по второму закону Кирхгофа необ­ходимо соблюдать следующее правило знаков:

а) если ток по направлению совпадает с выбранным направлени­ем обхода контуров, то соответствующее произведение IR входит в уравнение со знаком плюс, в противном случае произведение IR входит в уравнение со знаком минус,

б) если ЭДС повышает потенциал в направлении обхода контура, т.е. если при обходе контура приходится идти от минуса к плюсу внутри источника, то соответствующая ЭДС входит в уравнение со знаком плюс, в противном случае - со знаком минус.

По второму закону Кирхгофа имеем соответственно для контуров AR ₁ BR ₂ A, AR ₁ BR ₃ A, AR ₃ BR ₄ A:

I ₁ R ₁ - I ₂ R ₂ =ε ₁ - ε₂ (1)

I ₁ R ₁- I ₃ R ₃ = ε ₁ (2)

I ₃ R ₃ + I ₄ R ₄ = 0. (3)

Подставив в равенства (1)-(3) значения сопротивлений и ЭДС, получим систему уравнений:

I ₁ +I ₂ +I ₃ -I ₄ = 0,

2 I ₁ - 4 I ₂=6,

2 I ₁ - 4 I ₃=10,

4 I ₃ + 2 I ₄=0.

Поскольку нужно найти только два тока, то удобно воспользо­ваться методом определителей (детерминантов). С этой целью пере­пишем уравнения еще раз в следующем виде:

I ₁ +I ₂ +I ₃ -I ₄ = 0,

2 I ₁ - 4 I ₂+0+0=6,

2 I ₁+0 - 4 I ₃+0=10,

0+0+4 I ₃ + 2 I ₄=0.

Искомые значения токов найдем из выражений

I ₂ = Δ _{I 2}/Δи I ₃ = Δ_I3/Δ,

где Δ- определитель системы уравнений; Δ_I2и Δ_I3 - определители, полученные заменой соответствующих столбцов определителя А столбцами, составленными из свободных членов четырех вышеприведенных уравнений, находим

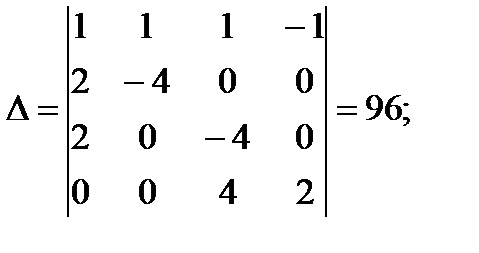
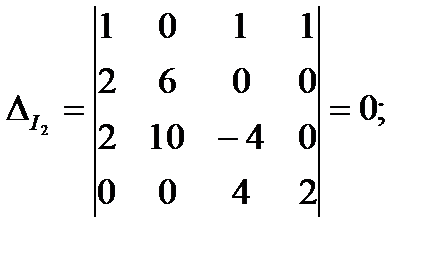
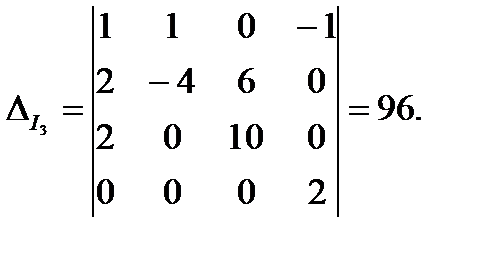
Отсюда получаем

I ₂=0; I ₃ = -1 А.

Знак минус у значения силы тока I ₃ свидетельствует о том, что при произвольном выборе направлений токов, указанных на рисунке, направление тока I ₃было указано противоположно истинному. На самом деле ток I ₃ те­чет от узла В к узлу А.

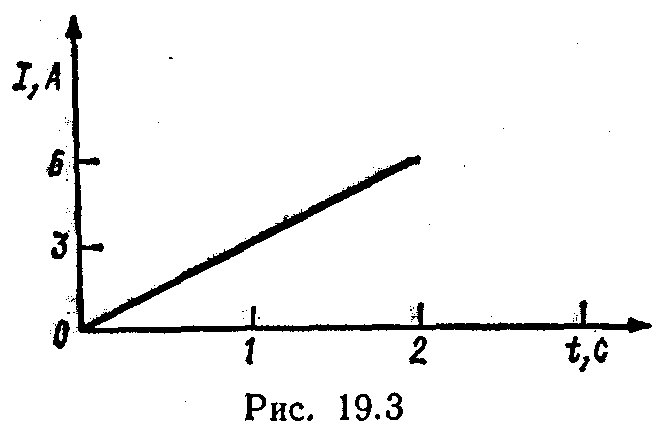Пример 4. Сила тока в про­воднике сопротивлением R= 20 Ом нарастает в течение вре­мени Δt=2 с по линейному за. кону от I ₀=0 до I _max=6 А (рис. 19.3). Определить количество теплоты Q ₁, выделившееся в этом проводнике за первую секунду, и Q ₂ - за вторую, а также найти отношение этих количеств теплоты Q ₂/ Q ₁.

Р е ш е н и е. Закон Джоуля - Ленца Q= I ² Rt применим в случае постоянного тока (I =const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде

d Q= I ² R d t. (1)

Здесь сила тока I является некоторой функцией времени. В на­шем случае

I=kt, (2)

где k - коэффициент пропорциональности, равный отношению приращений силы тока к интервалу времени, за который произошло это приращение:

k= Δ I/ Δ t.

С учетом равенства (2) формула (1) примет вид

d Q=k ² Rt ²d t. (3)

Для определения количества теплоты, выделившегося за конечный промежуток времени Δ t, выражение (3) следует проинтегрировать в пределах от t ₁до t ₂:

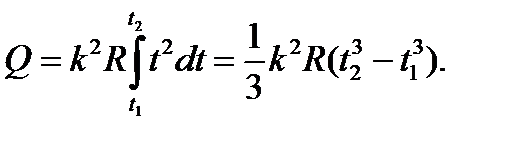
При определении количества теплоты, выделившегося за первую секунду, пределы интегрирования t ₁=О, t ₂ = 1 с и, следовательно,

Q ₁=60 Дж,

а за вторую секунду - пределы интегрирования t ₁= 1 с, t ₂ =2 с и тогда

Q₂=420 Дж.

Следовательно,

Q ₂/ Q ₁ =7,

т. е. за вторую секунду выделится теплоты в 7 раз больше, чем за первую секунду.

 

ЭЛЕКТРОМАГНЕТИЗМ

 

МАГНИТНОЕ ПОЛЕ ПОСТОЯННОГО ТОКА

 

Основные формулы

· Закон Био — Савара — Лапласа

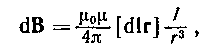
где dB — магнитная индукция поля, создаваемого элементом i водника с током; m — магнитная проницаемость; m₀ — магнитная постоянная (m₀ =4p · 10 ^-7 Гн/м); dl — вектор, равный по модулю длине dl проводника и совпадающий по направлению с током (элемент проводника); I — сила тока; r — радиус-вектор, проведенный от середины элемента проводника к точке, магнитная индукция в которой определяется.

Модуль вектора d B выражается формулой

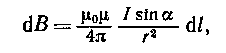
где a — угол между векторами d l и r.

· Магнитная индукция В связана с напряженностью Н магнитного поля (в случае однородной, изотропной среды) соотношением

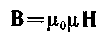
или в вакууме

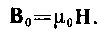
· Магнитная индукция в центре кругового проводника с током

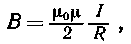
где R — радиус кривизны проводника.

· Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током,

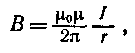где r — расстояние от оси проводника.

Магнитная индукция поля, создаваемого отрезком проводником

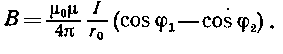
Обозначения ясны из рис. 21.1, а. Вектор индукции В перпенди­кулярен плоскости чертежа, направлен к нам и поэтому изображен точкой.

При симметричном расположении концов проводника относи­тельно точки, в которой определяется магнитная индукция (рис. 21.1, б), 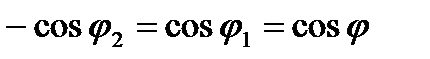и, следовательно,

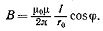
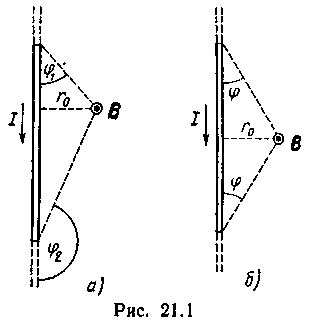· Магнитная индукция поля, создаваемого соленоидом в сред­ней его части (или тороида на его оси),

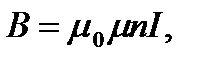
где п — число витков, приходящих­ся на единицу длины соленоида; I — сила тока в одном витке.

· Принцип суперпозиции маг­нитных полей: магнитная индук­ция В результирующего поля равна векторной сумме магнитных индукций В ₁, В₂,..., В _n складываемых полей, т. е.

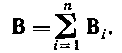
В частном случае наложения двух полей

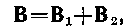
а модуль магнитной продукции

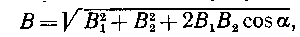
где a — угол между векторами В₁ и В₂.

Примеры решения задач

Пример 1. Два параллельных бесконечно длинных провода, по которым текут в одном направлении токи I =60 А, расположены на

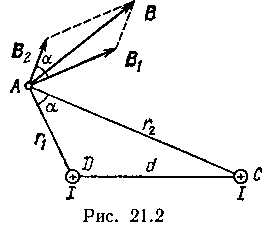
расстоянии d= 10см друг от друга. Определить магнитную индукцию В в точке, отстоящей от одного про­водника на расстоянии г₁=5 см и от другого — на расстоянии r₂ = 12см.

Решение. Для нахождения магнитной индукции в указанной точ­ке А (рис. 21.2) определим направле­ния векторов индукций В ₁ и В ₂ по лей, создаваемых каждым проводни­ком в отдельности, и сложим их геометрически, т. е. B=B ₁+ B ₂.Модуль индукции найдем по теоре­ме косинусов:

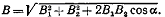
Значения индукций Bi и В₂ выражаются соответственно через силу тока I и расстояния r₁ и r₂ от провода до точки, индукцию

в которой мы вычисляем: 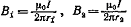Подставляя B₁ и В₂ в формулу (1) и вынося 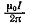за знак корня, получим

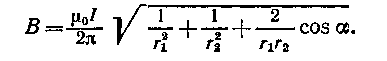(2)

Убедимся в том, что правая часть этого равенства дает единицу магнитной индукции (Тл):

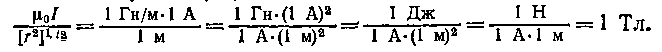
Здесь мы воспользовались определяющей формулой для маг­нитной индукции (В=М_mак /р_п). Откуда следует, что

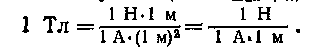
Вычисляем cosa. Заметим, что a = /_ DAC. Поэтому по теореме косинусов запишем 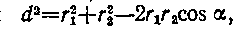, где d — расстояние между проводами. Отсюда

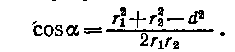
Подставив данные, вычислим значение косинуса: cos a = 0,576.

Подставив в формулу (2) значения m₀, I, r₁, r₂и cos b, найдем В =286 мкТл.

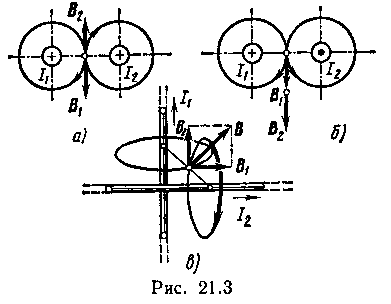
Пример 2. По двум длинным прямолинейным проводам, находя­щимся на расстоянии r=5 см друг от друга в воздухе, текут токи I =10 А каждый. Определить магнитную индукцию В поля, создаваемого то­ками в точке, лежащей по­середине между проводами, для случаев: 1) провода параллельны, токи текут в одном направлении (рис. 21.3, а); 2) провода парал­лельны, токи текут в про­тивоположных направле­ниях (рис. 21.3, б); 3) про­вода перпендикулярны, на­правление токов указано на рис. 21.3, в.

Решение: Результирующаяиндукция магнитного поля равна векторной сумме: B=B₁+B₂, где B₁ — индукция поля, создаваемого током 1 ₁; В₂ — индукция поля создаваемого током I ₂.

Если B₁ и В₂ направлены по одной прямой, то векторная сумма может быть заменена алгебраической суммой:

В=В₁+В₂. (1)

При этом слагаемые В₁ и В₂ должны быть взяты с соответствую­щими знаками. В данной задаче во всех трех случаях модули индукций В₁ и В₂ одинаковы, так как точки выбраны на равных расстояниях от про­водов, по которым текут равные токи. Вычислим эти индукции по формуле

B= m₀ I /(2pr). (2)

Подставив значения величин в формулу (2), найдем модули В₁ и В₂:

В₁=В₂=80 мкТл.

1-й случай. Векторы B₁ и В₂ направлены по одной прямой (рис. 21.3, а); следовательно, результирующая индукция В опреде­ляется по формуле (1). Приняв направление вверх положительным, вниз — отрицательным, запишем: В ₁ =— 80 мкТл, В ₂=80 мкТл.

Подставив в формулу (1) эти значения В ₁и B ₂, получим

В=В ₁ +В₂=0.

2-й случай. Векторы В ₁ и В ₂ направлены по одной прямой в одну сторону (рис. 21.3, б). Поэтому можем за­писать

В ₁ =В ₂ =— 80 мкТл.

Подставив в формулу (1) значения B ₁ и В ₂ получим

В=В ₁ +В ₂ =— 160 мкТл.

3-й случай. Векторы индукций магнит­ных полей, создаваемых токами в точке, лежащей посередине между проводами, взаимно перпендикулярны (рис. 21.3, в). Результирующая индукция по модулю и направлению является диагональю квадра­та, построенного на векторах В ₁ и В ₂. По теореме Пифагора найдем

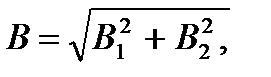(3)

Подставив в формулу (3) значения В ₁и В ₂и вычислив, получим Рис. 21.4 B =113 мкТл.

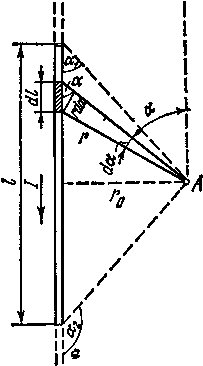Пример 3. Определить магнитную индукцию В поля, создаваемо­го отрезком бесконечно длинного прямого провода, в точке, равно­удаленной от концов отрезка и находящейся на расстоянии r ₀ =20 см от середины его (рис. 21.4). Сила тока I, текущего по про­воду, равна 30 А, длина l отрезка равна 60 см.

Решение. Для определения магнитной индукции поля, соз­даваемого отрезком провода, воспользуемся законом Био — Савара—

— Лапласа:

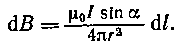(1)

 

Прежде чем интегрировать выражение (1), преобразуем его так, чтобы можно было интегрировать по углу a. Выразим длину элемента d l проводника через da. Согласно рис. 21.4, запишем

 

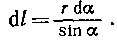
Подставим это выражение d l в формулу (1): Рис. 21.4

 

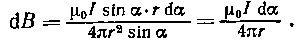
Но r — величина переменная, зависящая от a и равная 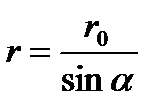Подставив rв предыдущую формулу, найдем

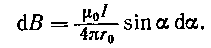(2)

Чтобы определить магнитную индукцию поля, создаваемого от­резком проводника, проинтегрируем выражение (2) в пределах от a₁ до a₂:

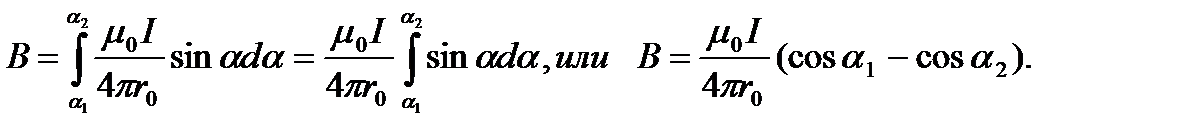(3)

Заметим, что при симметричном расположении точки A относитель­но отрезка провода cos a₂= – cos a₁. С учетом этого формула (3) примет вид

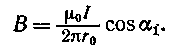(4)

 

Из рис. 21.4 следует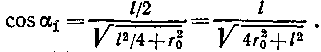

Подставив выражение cos a₁ в формулу (4), получим

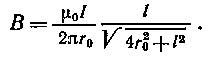(5)

Подставим числовые значения в формулу (5) и произведем вы­числения:

 

 

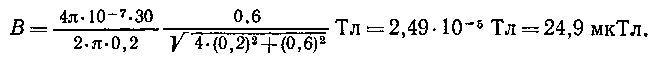
CИЛА, ДЕЙСТВУЮЩАЯ НА ЗАРЯД, ДВИЖУЩИЙСЯ В МАГНИТНОМ ПОЛЕ

Основные формулы

• Сила F, действующая на заряд Q, движущийся со скоростью v в магнитном поле с индукцией В (сила Лоренца), выражается фор­мулой

F= Q [ v B ] или F=|Q|uB sina,

где a — угол, образованный вектором скорости v движущейся ча­стицы и вектором В индукции магнитного поля.

 

Примеры решения задач

Пример 1. Электрон, пройдя ускоряющую разность потенциа­лов U =400 В, попал в однородное магнитное поле с индукцией B =1,5 мТл. Определить: 1)радиус R кривизны траектории; 2)ча­стоту п вращения электрона вмагнитном поле. Вектор скорости электрона перпендикулярен линиям индукции.

Решение. 1. Радиус кривизны траектории электрона опре­делим, исходя из следующих соображений: на движущийся в маг­нитном поле электрон действует сила Лоренца F. (Действием силы тяжести можно пренебречь.) Вектор силы Лоренца перпендикуля­рен вектору скорости и, следовательно, по второму закону Ньютона, сообщает электрону нормальное ускорение а_n : F=ma_n. Подставив сюда выражения F и а_n, получим

| e | uB sin a=mu²/R, (1)

где е, u, т — заряд, скорость, масса электрона; В — индукция маг­нитного поля; R — радиус кривизны траектории; a — угол между направлениями векторов скорости v и индукции В (в нашем случае v ^ B и a = 90°, sin a =l).

Из формулы (1) найдем

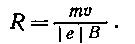(2)

Входящий в выражение (2) импульс mu выразим через кинетическую энергию Т электрона:

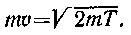(3)

Но кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U, определяется равенством Т= | e | U. Подставив это выражение Т в формулу (3), получим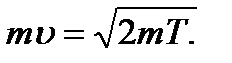

Тогда выражение (2) для радиуса кривизны приобретает вид

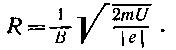
Убедимся в том, что правая часть этого равенства дает единицу длины (м):

После вычисления по формуле (4) найдем

R =45 мм.

2. Для определения частоты вращения воспользуемся формулой связывающей частоту со скоростью и радиусом кривизны траектории,

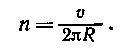
Подставив R из выражения (2) в эту формулу, получим

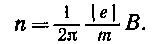
Произведя вычисления, найдем n =4,20 × 10⁷ c^-1 .

Пример 2. Электрон, имея скорость u =2 Мм/с, влетел воднородное магнитное поле с индукцией В =30 мТл под углом a=30° к направлению линий индукции. Определить радиус R и шаг h винтовой линии, покоторой будет двигаться электрон.

Решение. Известно, что на заряженную частицу, влетевшую в магнитное поле, действует сила Лоренца, перпендикулярная векторам магнитной индукции В и скорости v частицы:

F=QuB sin a, (1)

где Q — заряд частицы.

В случае, если частицей является электрон, формулу (1) можно записать в виде

F= |e| uB sin a.

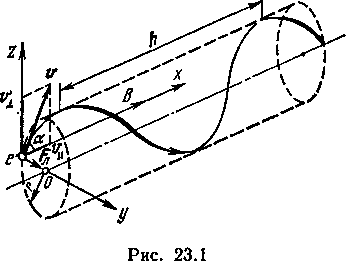Так как вектор силы Лоренца перпендикулярен вектору скоро­сти, то модуль скорости не будет изменяться под действием этой силы. Но при постоянной скорости, как это следует из формулы (1), останется постоянным и значение силы Лоренца. Из механики известно, что постоянная си­ла, перпендикулярная скоро­сти, вызывает движение по окружности. Следовательно, электрон, влетевший в маг­нитное поле, будет двигаться по окружности в плоскости, перпендикулярной линиям индукции, со скоростью, рав­ной поперечной составляю­щей u ₁скорости (рис. 23.1); одновременно он будет дви­гаться и вдоль поля со ско­ростью u _||:

u _|| = u sin a, u _|| = u cos a.

В результате одновременного участия в движениях по окружно­сти и по прямой электрон будет двигаться по винтовой линии.

Радиус окружности, по которой движется электрон, найдем сле­дующим образом. Сила Лоренца F сообщает электрону нормальное ускорение а_п. По второму закону Ньютона, F=ma_n, где F= | e | u ₁ B и a_n=u ² ^ R,. Тогда

| e | u ^ B = mu₂²/R,

откуда после сокращения на u _zнаходим радиус винтовой линии:

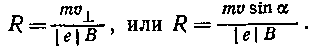
Подставив значения величин т, u, e, В и a и произведя вычисле­ния, получим

R =0,19 мм.

Шаг винтовой линии равен пути, пройденному электроном вдоль поля со скоростью u _x завремя, которое понадобится электрону для того, чтобы совершить один оборот,

h = u _|| T (2)

где T=2pR/u _^ — период вращения электрона. Подставив это выра­жение для Т в формулу (2), найдем

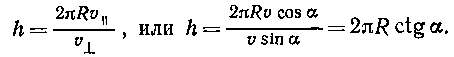
Подставив в эту формулу значения величин p, R и a и вычислив, получим

h =2,06 мм.

Пример 3. Электрон движется воднородном магнитном поле с индукцией В=0,03 Тл поокружности радиусом r=10см. Опреде­лить скорость u электрона.

Решение. Движение электрона по окружности в однородном магнитном поле совершается под действием силы Лоренца (см. примеры 1 и 2). Поэтому можно написать

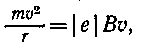(1)

откуда найдем импульс электрона:

р=тu= | е | Вr. (2)

Релятивистский импульс выражается формулой

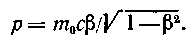
Выполнив преобразования, получим следующую формулу для определения скорости частицы:

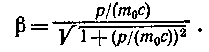(3)

В данном случае р= | e | Br. Следовательно,

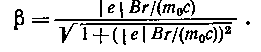
В числитель и знаменатель формулы (4) входит выражение |е| В_r(т ₀ с). Вычислим его отдельно:

|е| В_r / (m ₀c) = 1,76.

Подставив найденное значение отношения |е| В_r(т ₀ с) в формулу (4), получим

b = 0,871, или u = с b= 2,61-10⁸ м/с.

Электрон, обладающий такой скоростью, является релятивистским (см. § 5).

Пример 4. Альфа-частица прошла ускоряющую разность потенциалов U =104 В и влетела в скрещенные под прямым углом электрическое (E =10 кВ/м) и магнитное (B =0,1 Тл) поля. Найти отношение заряда альфа-частицы к ее массе, если, двигаясь перпендикулярно обоим полям, частица не испытывает отклонений от прямолинейной траектории.

Решение. Для того чтобы найти отношение заряда Q альфа-частицы к ее массе m, воспользуемся связью между работой сил электрического поля и изменением кинетической энергии частиц:

QU = mu ²/2,

откуда

Q/m=u²/(2U). (1)

Скорость u альфа-частицы найдем из следующих соображений. В скрещенных электрическом и магнитном полях на движущуюся заряженную частицу действуют две силы:

а) сила Лоренца F _л=Q[ vВ ], направленная перпендикулярно скорости v и вектору магнитной индукции В;

б) кулоновская сила F_K =Q E, сонаправленная с вектором напряженности Е электростатического поля (Q >0).

Сделаем рисунок с изображением координатных осей и векторных

величин. Направим вектор магнитной индукции В вдоль оси О_z (рис. 23.2), скорость v—в положительном направлении оси Ох, тогда F _л и F _k будут направлены так, как это указано на ри­сунке.

Альфа-частица не будет испытывать отклонения, если геометри­ческая сумма сил F _л+ F_k будет равна нулю. В проекции на ось

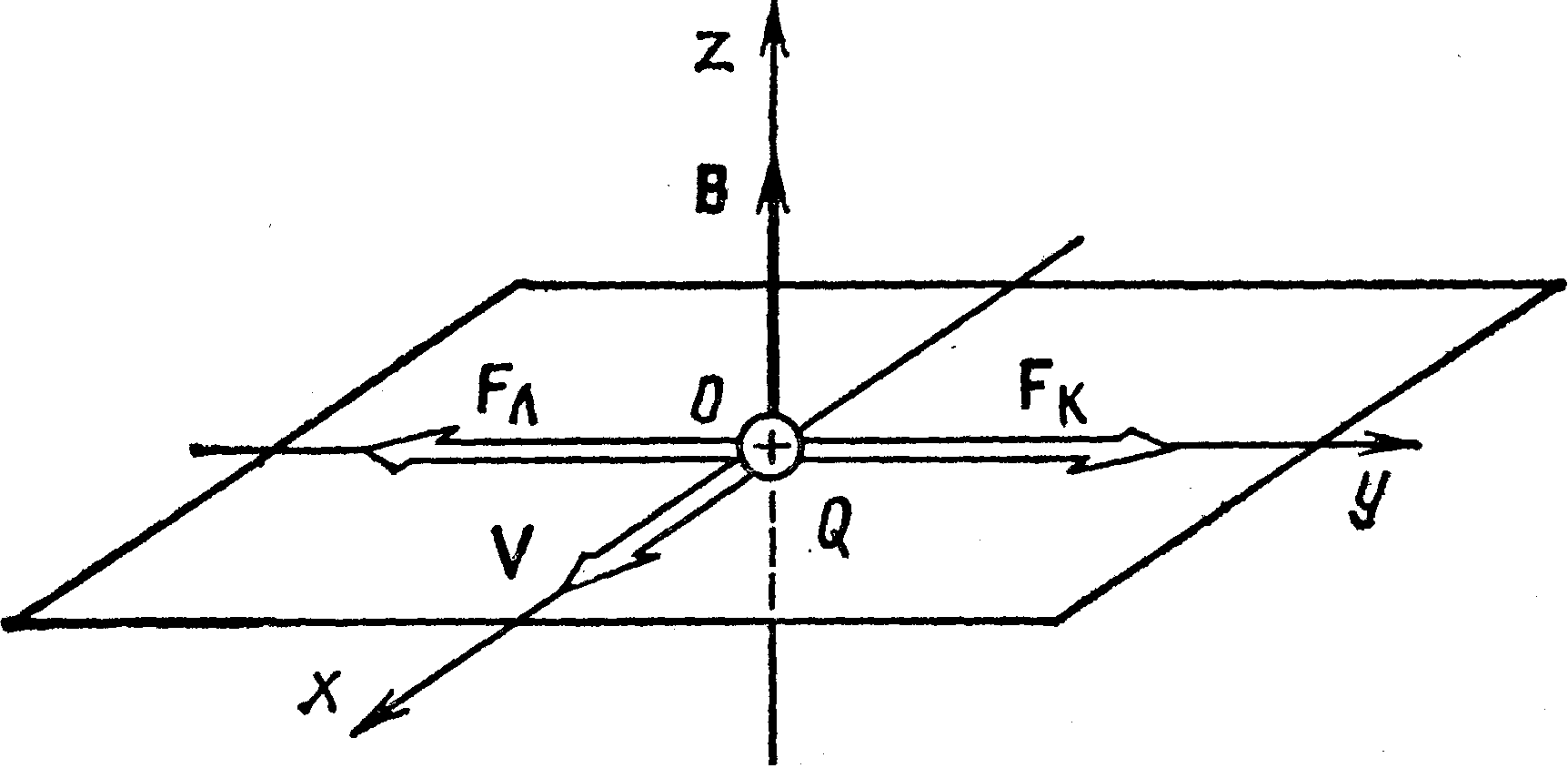
Рис. 23.2

Оу получим следующее равенство (при этом учтено, что вектор ско­рости v перпендикулярен вектору магнитной индукции В и Sin (v ^Ù B)=l):

QE—QuB = O,

откуда

u =E/B.

Подставив это выражение скорости в формулу (1), получим

Q/m=E²(2UB²).

Убедимся в том, что правая часть равенства дает единицу отно­шения заряда к массе (Кл/кг):

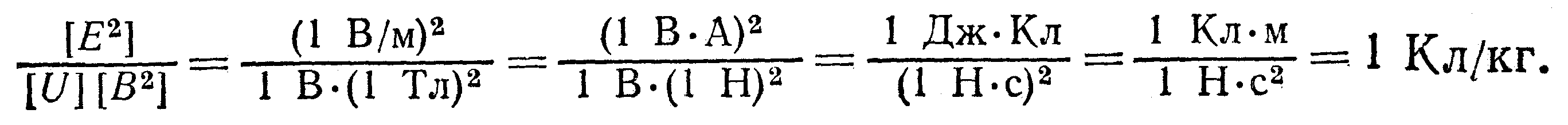
Произведем вычисления: