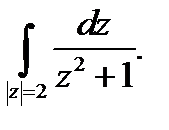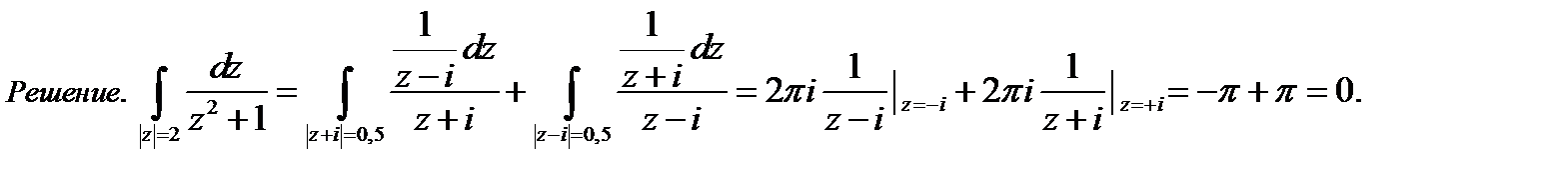Лекция 5
Интеграл от функции комплексного переменного
Определение 1. Пусть 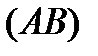 – непрерывная кривая на комплексной плоскости (замкнутая или нет), и пусть вдоль этой кривой задана некоторая функция комплексного переменного
– непрерывная кривая на комплексной плоскости (замкнутая или нет), и пусть вдоль этой кривой задана некоторая функция комплексного переменного 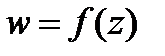 . Разобьем
. Разобьем 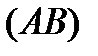 произвольным образом на части точками
произвольным образом на части точками 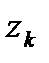 , и на каждой дуге разбиения выберем произвольную точку
, и на каждой дуге разбиения выберем произвольную точку 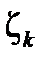 (можно и на краю этой дуги) (рис. 1):
(можно и на краю этой дуги) (рис. 1):

Рис.1
Составим интегральную сумму 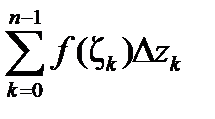 , где
, где 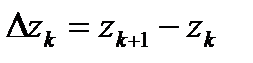 . Обозначим через
. Обозначим через 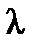 максимальную по
максимальную по 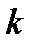 длину вектора
длину вектора 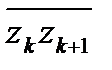 . Если существует предел наших интегральных сумм при
. Если существует предел наших интегральных сумм при 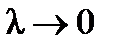 , который не зависит от выбора точек
, который не зависит от выбора точек 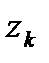 и
и 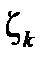 , то этот предел называется интегралом от функции комплексного переменного
, то этот предел называется интегралом от функции комплексного переменного 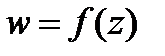 вдоль кривой
вдоль кривой 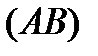 и обозначается
и обозначается 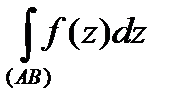 . Таким образом,
. Таким образом,
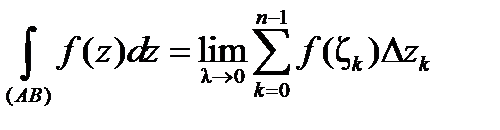 . (1)
. (1)
Пусть 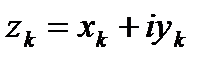 ,
, 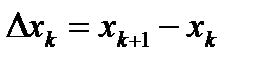 ,
, 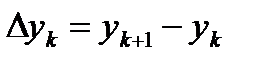 , тогда
, тогда
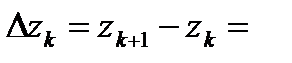
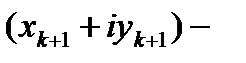
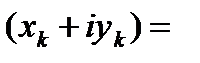
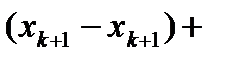
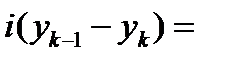
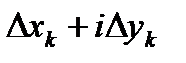 .
.
Пусть 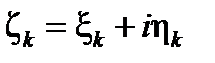 . Обозначая
. Обозначая 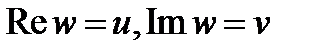 , имеем:
, имеем:
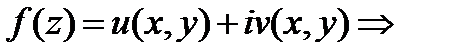
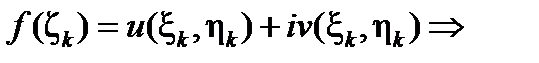
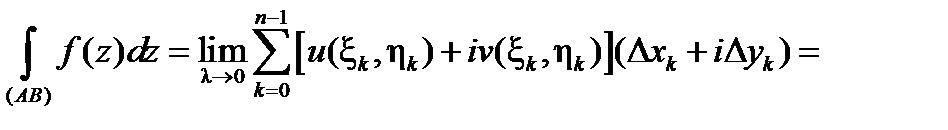
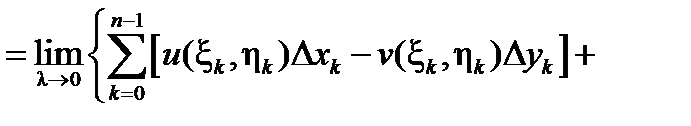
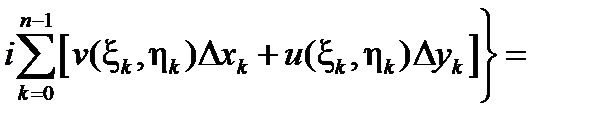
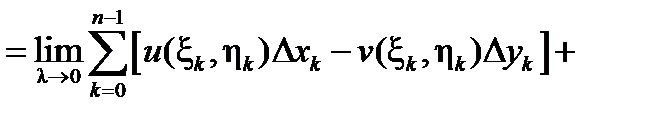
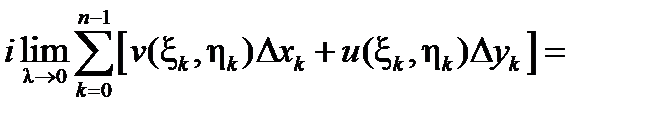
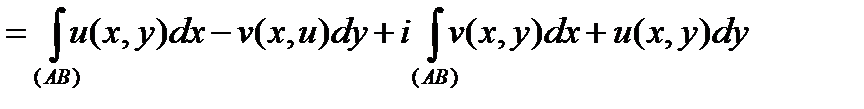
при условии существования этих криволинейных интегралов (второго рода).
Таким образом, нами доказана следующая теорема:
Теорема 1 (существование и вычисление интеграла от функции комплексного переменного).
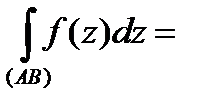
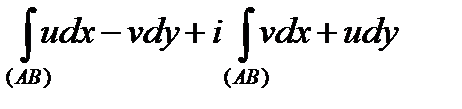 (2) при условии существования криволинейных интегралов в правой части этой формулы.
(2) при условии существования криволинейных интегралов в правой части этой формулы.
Запомнить формулу (2) проще всего при помощи следующей формальной выкладки: 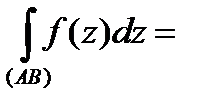
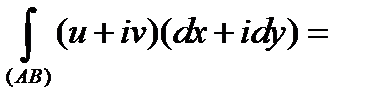
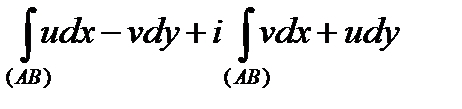 .
.
Если  задана параметрическими уравнениями
задана параметрическими уравнениями 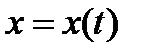 ,
, 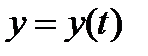 ,
, 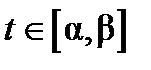 , функции
, функции 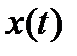 и
и 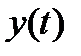 непрерывно дифференцируемы на
непрерывно дифференцируемы на 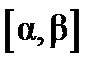 , при изменении
, при изменении 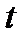 от
от 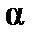 до
до 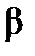 кривая описывается в направлении от
кривая описывается в направлении от 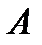 к
к 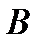 (не обязательно
(не обязательно 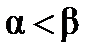 ), функции
), функции 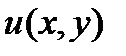 и
и 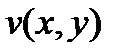 непрерывны на
непрерывны на 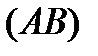 , то интегралы в правой части формулы (2) существуют и
, то интегралы в правой части формулы (2) существуют и
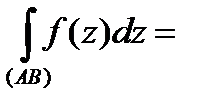
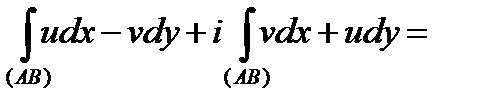
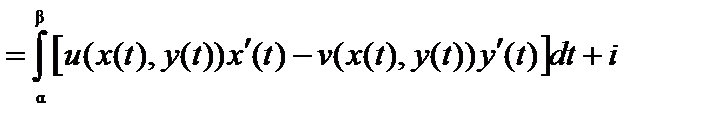
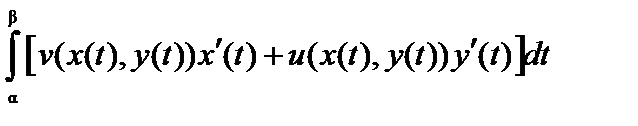 . (3)
. (3)
Пример. Вычислить 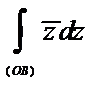 , где 0 – начало координат, В:
, где 0 – начало координат, В: 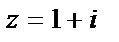 , а путь интегрирования:
, а путь интегрирования: 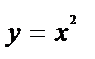 (рис. 2).
(рис. 2).
Решение. 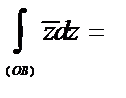
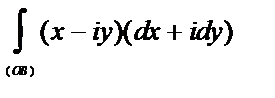
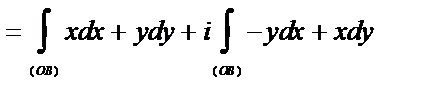
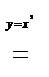
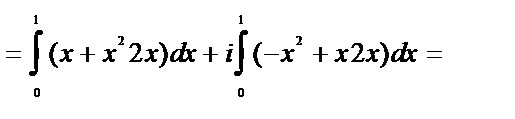
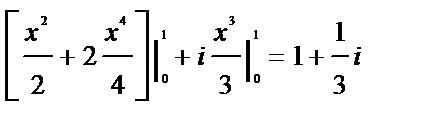 .
.
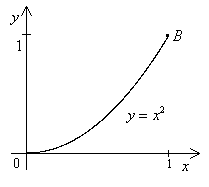
Рис. 2
Уравнения кривой 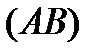
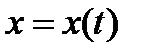 ,
, 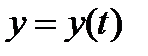 ,
, 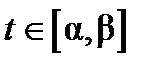 можно записать в виде
можно записать в виде 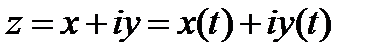 , т.е.
, т.е. 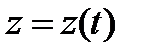 ,
, 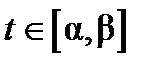 , при этом
, при этом 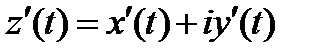 .
.
Формулу (3) можно переписать следующим образом:
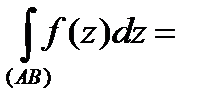
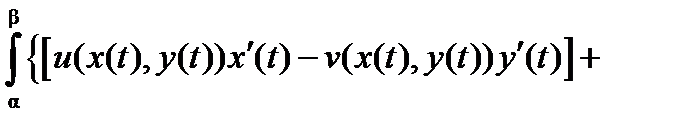
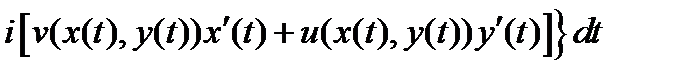 .
.
Легко видеть, что функция в фигурных скобках в правой части последней формулы равна 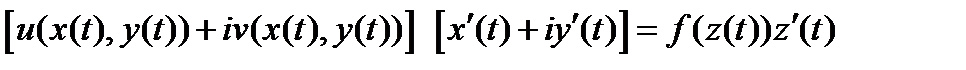 , и, таким образом,
, и, таким образом,
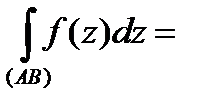
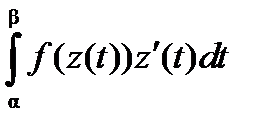 (4)
(4)
(мы получили формулу (4) при помощи формальных преобразований; на самом деле, если рассмотреть комплексно-значные функции действительного переменного 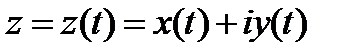 и их производные
и их производные 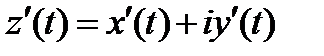 , то эти преобразования будут иметь вполне строгий характер).
, то эти преобразования будут иметь вполне строгий характер).
Задача. Показать что
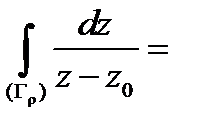
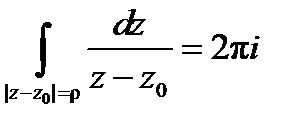 , (5)
, (5)
где 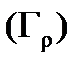 - окружность радиуса
- окружность радиуса 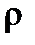 с центром в точке
с центром в точке 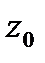 (как и обычно, при отсутствии указания на направление обхода контура это направление берется положительным, т.е. для правой системы координат
(как и обычно, при отсутствии указания на направление обхода контура это направление берется положительным, т.е. для правой системы координат 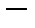 против часовой стрелки).
против часовой стрелки).
Решение. Зададим контур 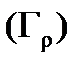 параметрически:
параметрически: 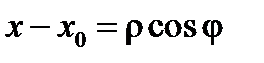 ,
, 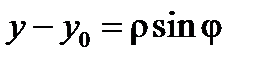 (при таком задании, как раз,
(при таком задании, как раз, 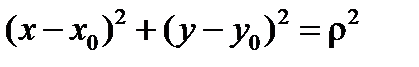 ). При этом
). При этом 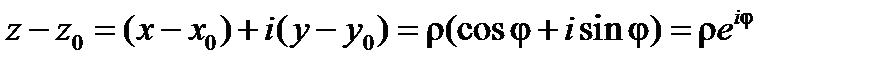 , т.е.
, т.е. 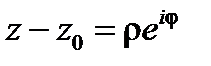 ,
, 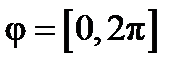 . Тогда
. Тогда 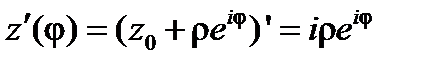 и по формуле (4)
и по формуле (4) 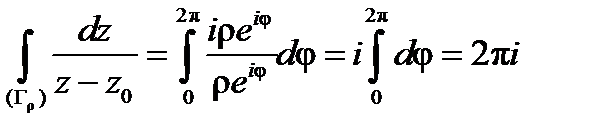 .
.
Основные свойства интегралов от функций комплексного переменного
Сначала при условии существования интегралов укажем три свойства, которые следуют из аналогичных свойств криволинейного интеграла и определения 1:
1. Для любых комплексных чисел 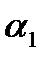 и
и 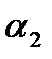
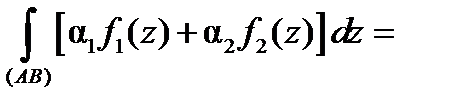
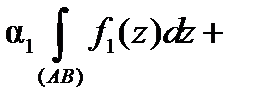
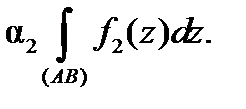

2. 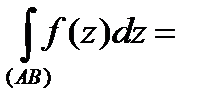
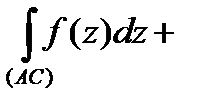
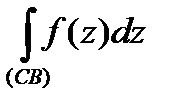 (рис. 3).
(рис. 3).
Рис. 3
3. 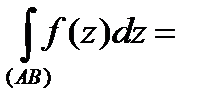
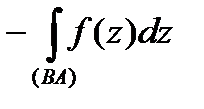 .
.
4. Теорема 2. Пусть 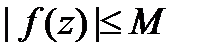 для
для 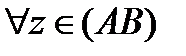 и
и 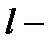 длина кривой
длина кривой 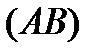 . Тогда при условии существования интеграла:
. Тогда при условии существования интеграла:
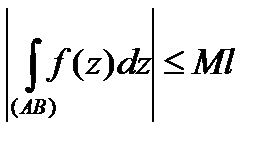 . (6)
. (6)
 Можно проверить, что для комплексных чисел, как и для действительных чисел,
Можно проверить, что для комплексных чисел, как и для действительных чисел,
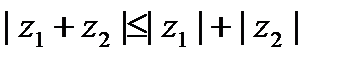 ,
, 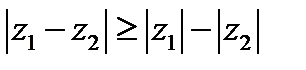 ,
, 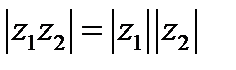 ,
, 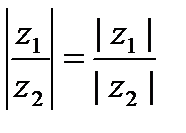 .
.
Из определения 1, 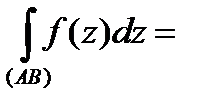
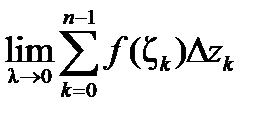 . Отсюда имеем:
. Отсюда имеем:
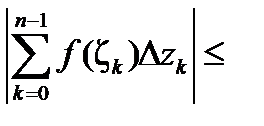
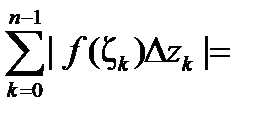
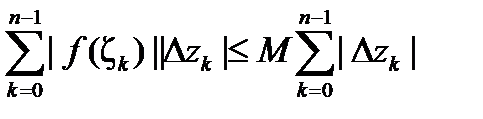 .
.
Здесь 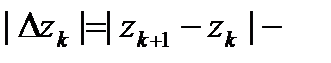 это расстояние на комплексной плоскости между точками
это расстояние на комплексной плоскости между точками 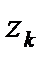 и
и 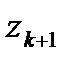 , а
, а 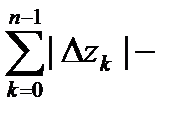 сумма таких расстояний, т.е. длина ломаной, вписанной в дугу
сумма таких расстояний, т.е. длина ломаной, вписанной в дугу 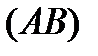 (рис. 4). Но длина всякой вписанной ломаной не превосходит длины самой дуги, значит,
(рис. 4). Но длина всякой вписанной ломаной не превосходит длины самой дуги, значит, 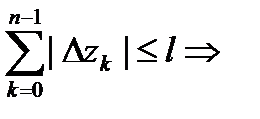
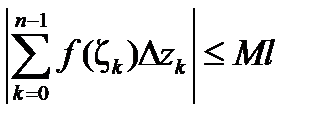 , откуда при
, откуда при 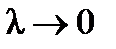
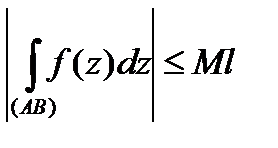 . ■
. ■
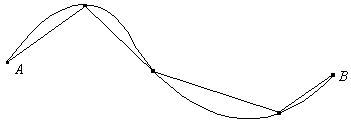
Рис. 4
Теорема 3 (интегральная теорема Коши). Пусть функция 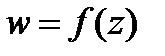 аналитическая в односвязной области
аналитическая в односвязной области 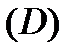 и
и 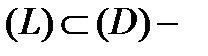 кусочно-гладкая замкнутая кривая. Тогда
кусочно-гладкая замкнутая кривая. Тогда 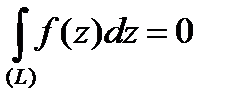 .
.
 Вспомним формулу (2): при
Вспомним формулу (2): при 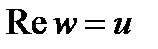 и
и 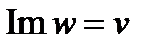
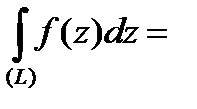
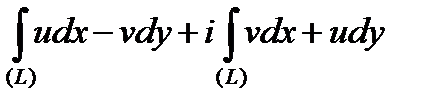 . Два последних криволинейных интеграла удовлетворяют условию независимости криволинейного интеграла второго рода от формы пути интегрирования
. Два последних криволинейных интеграла удовлетворяют условию независимости криволинейного интеграла второго рода от формы пути интегрирования 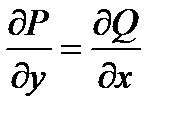 , при выполнении которого
, при выполнении которого 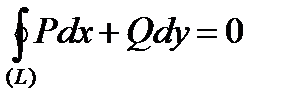 :
:
для первого из них 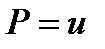 ,
, 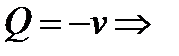
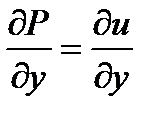 ,
, 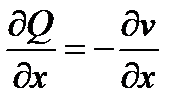 ,
,
для второго же 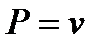 ,
, 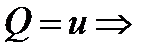
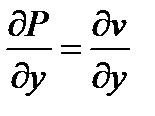 ,
, 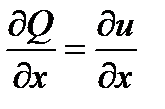 ,
,
а 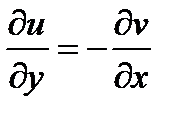 и
и 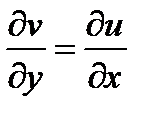 , так как аналитическая функция удовлетворяет условиям Коши-Римана. ■
, так как аналитическая функция удовлетворяет условиям Коши-Римана. ■
Следствие 1. Если функция 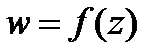 аналитична в односвязной области
аналитична в односвязной области 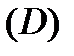 и
и 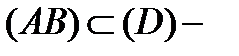 кусочно-гладкая кривая, то
кусочно-гладкая кривая, то 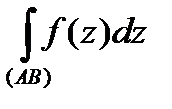 не зависит от формы пути
не зависит от формы пути 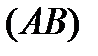 , а зависит лишь от положения ее начальной и конечной точек.
, а зависит лишь от положения ее начальной и конечной точек.
Следствие 2. Пусть функция 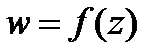 аналитична в односвязной области
аналитична в односвязной области 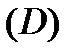 и
и 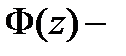 какая-либо ее первообразная в этой области, т.е.
какая-либо ее первообразная в этой области, т.е. 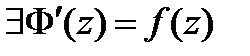 ,
, 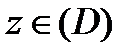 . Тогда для любых
. Тогда для любых 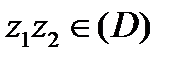
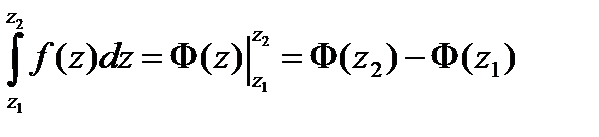 . (7)
. (7)
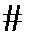 Пусть
Пусть 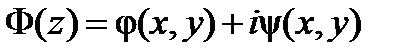 . Тогда по формулам нахождения производной
. Тогда по формулам нахождения производной 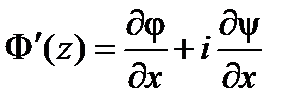 . Так как
. Так как 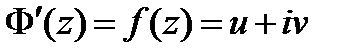 , то отсюда
, то отсюда 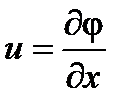 ,
, 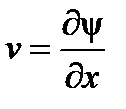 , тогда при
, тогда при 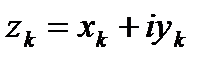 ,
, 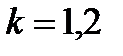 из формулы (2)
из формулы (2) 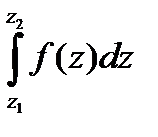
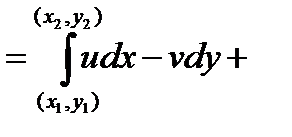
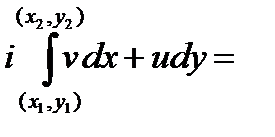 =
= 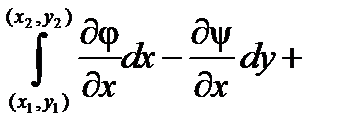
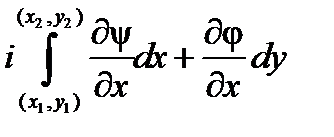 , что, согласно условиям Коши-Римана для аналитической функции
, что, согласно условиям Коши-Римана для аналитической функции 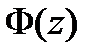 , равно
, равно 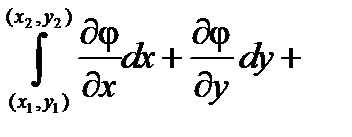
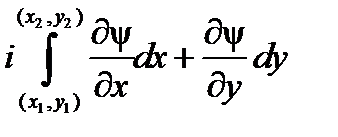 =
= 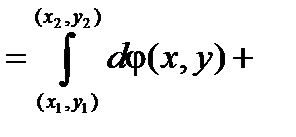
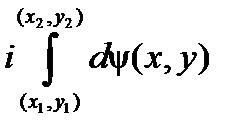 , а это, как было показано в теме «Криволинейные интегралы», равно
, а это, как было показано в теме «Криволинейные интегралы», равно 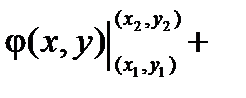
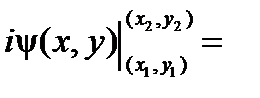
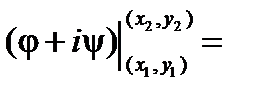
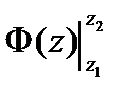 . ■
. ■
Пример. Найти 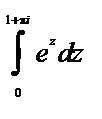 .
.
Решение. 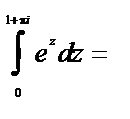
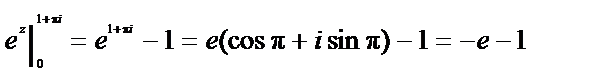 .
.
Теорема 4 (интегральная теорема Коши для неодносвязных областей). Пусть область 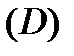 ограничена конечным числом кусочно-гладких кривых и функция
ограничена конечным числом кусочно-гладких кривых и функция 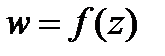 аналитическая в некоторой области
аналитическая в некоторой области 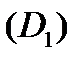 , включающей
, включающей  и всю ее границу (на рис. 5 сплошной линией изображена граница
и всю ее границу (на рис. 5 сплошной линией изображена граница  , а пунктиром – граница
, а пунктиром – граница  ).
).
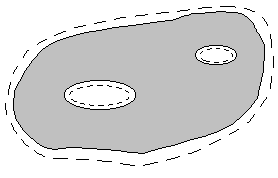
Тогда, если 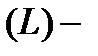 внешняя граница
внешняя граница 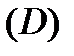 , а
, а 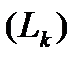 ,
, 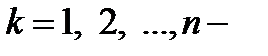 ее внутренние границы, то
ее внутренние границы, то
то 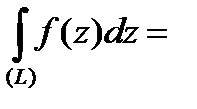
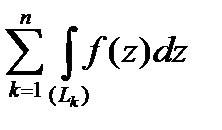 , где все интегралы берутся в одном направлении.
, где все интегралы берутся в одном направлении.
Рис. 5
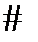 Взяв произвольные точки
Взяв произвольные точки 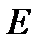 и
и 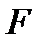 на контуре
на контуре 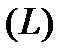 , проведем гладкие самонепересекающиеся кривые
, проведем гладкие самонепересекающиеся кривые 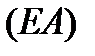 ,
, 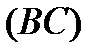 ,
, 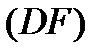 (на рис. 6
(на рис. 6 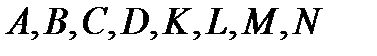 – произвольные точки внутренних границ). К двум получившимся односвязным областям применим теорему 3:
– произвольные точки внутренних границ). К двум получившимся односвязным областям применим теорему 3:
Рис. 6
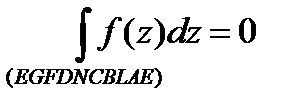 и
и 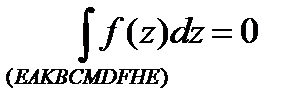 . Сложим эти два равенства. При этом интегралы по введенным перегородкам сокращаются, так как эти перегородки проходятся дважды, один раз в одном, другой раз в противоположном направлении. Получим:
. Сложим эти два равенства. При этом интегралы по введенным перегородкам сокращаются, так как эти перегородки проходятся дважды, один раз в одном, другой раз в противоположном направлении. Получим:
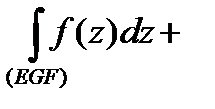
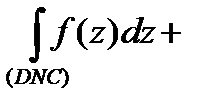
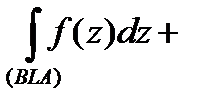
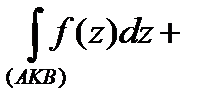
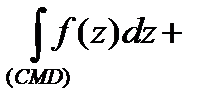
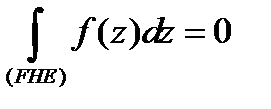 , т.е.
, т.е.
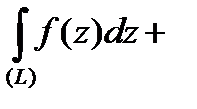
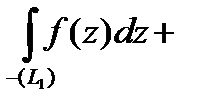
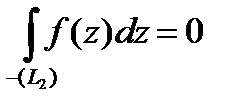 , или, учитывая, что
, или, учитывая, что 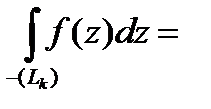
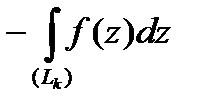 ,
, 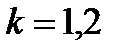 ,
, 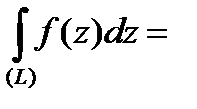
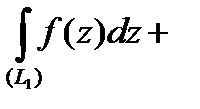
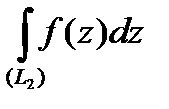 (здесь
(здесь 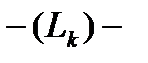 это контур
это контур 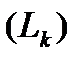 , проходимый в противоположном направлении).
, проходимый в противоположном направлении).
Аналогично для большего количества «дырок» и для противоположного направления обхода границ области 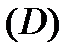 . ■
. ■
Теорема 5 (интегральная формула Коши). Пусть функция 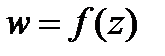 аналитическая в односвязной области
аналитическая в односвязной области 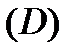 ,
, 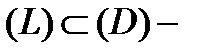 кусочно-гладкая замкнутая кривая и
кусочно-гладкая замкнутая кривая и 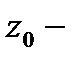 точка внутри этой кривой. Тогда
точка внутри этой кривой. Тогда
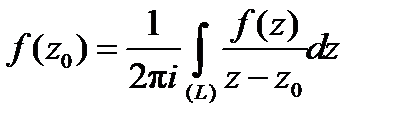 (8)
(8)
(направление обхода контура берется положительным).
 Мы будем доказывать, что
Мы будем доказывать, что 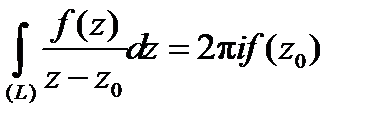 .
.
На рис. 7 «внешним» пунктиром изображена граница области  . Пусть
. Пусть 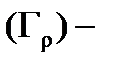 окружность радиуса
окружность радиуса 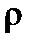 с центром в точке
с центром в точке 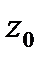 , целиком содержащаяся внутри
, целиком содержащаяся внутри  (для этого
(для этого 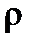 должно быть достаточно малым). В области, ограниченной «внешним» и любым «внутренним» (по отношению к
должно быть достаточно малым). В области, ограниченной «внешним» и любым «внутренним» (по отношению к 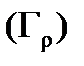 ), содержащим
), содержащим 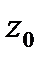 ,
,
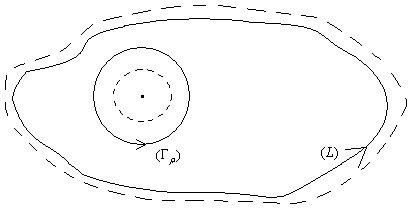
Рис. 7
пунктирами, функция 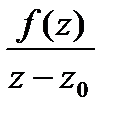 является аналитической (как отношение двух аналитических функций при знаменателе, отличном от 0), и по теореме 4
является аналитической (как отношение двух аналитических функций при знаменателе, отличном от 0), и по теореме 4 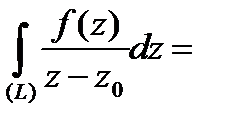
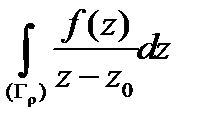 . Надо доказать, что последнее выражение равно
. Надо доказать, что последнее выражение равно 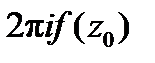 . Учитывая формулу (5), нам надо проверить, что
. Учитывая формулу (5), нам надо проверить, что 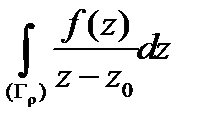
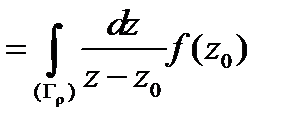 или
или
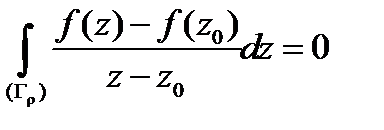 . (9)
. (9)
Для проверки (9) докажем, что интеграл в левой части этой формулы можно (за счет выбора  ) сделать сколь угодно малым. Пусть
) сделать сколь угодно малым. Пусть  сколь угодно малое число. Так как
сколь угодно малое число. Так как 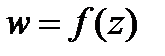 непрерывна в точке
непрерывна в точке 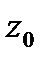 , то в некоторой окрестности этой точки
, то в некоторой окрестности этой точки 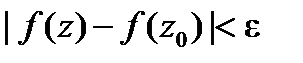 и, значит, для достаточно малых
и, значит, для достаточно малых 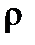 (таких, что окружность
(таких, что окружность 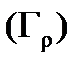 попадает в эту окрестность)
попадает в эту окрестность) 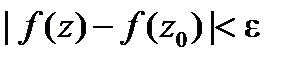 для
для 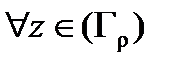 . Тогда
. Тогда
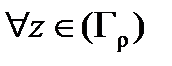
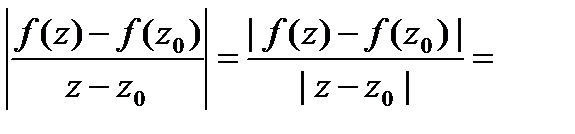
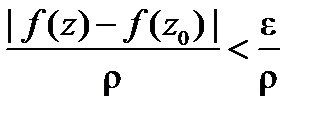 . Согласно формуле (6), при
. Согласно формуле (6), при 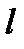 – длине
– длине 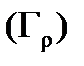 имеем:
имеем: 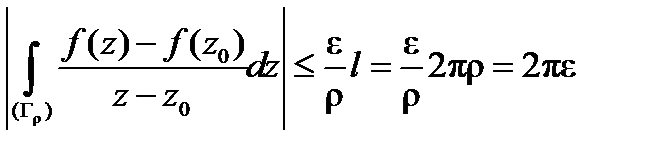 , а это число, действительно, сколь угодно мало. ■
, а это число, действительно, сколь угодно мало. ■
Пример. Вычислить 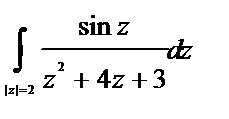 (направление обхода контура положительно; см. рис. 8).
(направление обхода контура положительно; см. рис. 8).
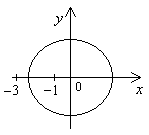
Рис. 8
Решение. 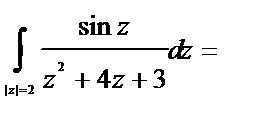
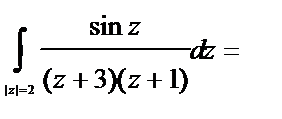
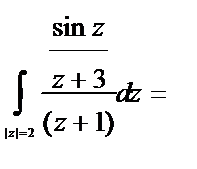
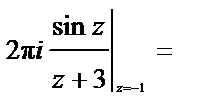
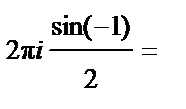
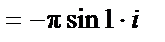 .
.
Интегральная формула Коши является основой для всей излагаемой ниже теории.
Пример. Вычислить