Тема «Параллельность в пространстве».

Тема «Параллельность в пространстве».

Параллельность прямых в пространстве.

Определение: Две прямые в пространстве называются параллельными, если они не пересекаются.

Определение: Две прямые в пространстве называются скрещивающимися, если они не пересекаются и не лежат в одной плоскости.

Взаимное расположение прямых в пространстве.

Пересекающиеся прямые	Скрещивающиеся прямые	Параллельные прямые

 

Теорема 1.1 Через точку вне данной прямой можно провести прямую, параллельную данной, и притом только одну.

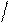
Дано: точка 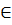А а

Доказать: 1)Что через т.А можно провести

2) Что единственная

Признак параллельности прямых.

Теорема 1.2 Две прямые, параллельные третьей прямой, параллельны.

Рассматриваем два случая.

Все прямые принадлежат одной плоскости	Прямые принадлежат разным плоскостям

 

Параллельность прямой и плоскости в пространстве.

Определение: Прямая и плоскость называются параллельными, если они не пересекаются.

Взаимное расположение прямой и плоскости в пространстве.

Прямая принадлежит плоскости	Прямая пересекает плоскость	Прямая параллельна плоскости

Признак параллельности прямой и плоскости.

Теорема 2.1. Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.

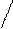
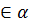Дано: а и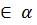

 

Доказать: а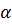

Параллельность плоскостей.

Определение: Плоскости называются параллельными, если они не пересекаются.

Взаимное расположение плоскостей в пространстве.

Пересекающиеся плоскости	Параллельные плоскости

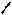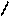
Признак параллельности плоскостей.

Теорема 3.1. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.

Дано: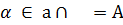

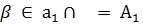
Доказать:

Существование плоскости параллельной данной.

Теорема 3.2. Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну.

Свойства параллельных плоскостей.

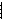1 свойство: Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.

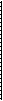
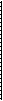
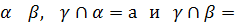а

 

2 свойство: Отрезки параллельных прямых, заключённые между двумя параллельными плоскостями, равны.

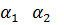а

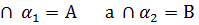а и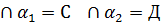

АВ СД

Задания для самостоятельного выполнения

Задание №1. Ответьте письменно на следующие вопросы:

1. Какие прямые называются параллельными?

2. Какие прямые называются скрещивающимися?

3. Назовите признак параллельности прямых в пространстве.

4. Какие прямые и плоскости называются параллельными?

5. Сколько прямых можно провести через точку, не лежащую на данной прямой?

6. Сформулируйте признак параллельности прямой и плоскости.

7. Какие плоскости называются параллельными?

8. Сформулируйте признак параллельности плоскостей.

9. Сколько плоскостей, параллельных данной, можно провести через точку, не лежащую на данной плоскости?

10. Какие два свойства параллельных плоскостей вы знаете?

Задание №2. Изобразите в тетради

1. Две параллельные прямые в плоскости

2. Три параллельные прямые не лежащие в одной плоскости.

3. Прямую АВ параллельную плоскость

4. Две параллельные плоскости 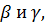плоскость, 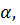которая пересекает обе эти плоскости по прямым АВ, СД.