Марковская цепь с непрерывным временем

Лекция 1. Цель и задачи дисциплины

Имитационное моделирование – один из основных методов анализа и синтеза сложных систем, возникающих при изучении экономических или физических процессов и объектов на микро, макро и глобальном уровнях.

Целью преподавания дисциплины «Имитационное моделирование» яв­ляется усвоение студентами основных понятий и мето­дов имитационного моделирования, необходимых в профессиональной деятельности специалиста в области применения математических методов в экономике.

Введение

Имитационным моделированием называется воспроизведение поведения изучаемой системы на основе анализа ее структуры и наиболее существенных взаимосвязей элементов с целью получения информации о функциональных свойствах этого объекта.

Модель системы представляет изучаемый объект и выступает в роли относительно самостоятельной системы, позволяющей получить важнейшие сведения о самом объекте.

Компьютерное ИМ предполагает выполнение ряда последовательных действий.

1) Описание реальной системы с выделением структуры, динамического взаимодействия элементов, факторов неопределенности и состояний системы, в которых она может находиться.

2) Создание блоковой схемы объекта с указанием состояний его элементов и возможных переходов между ними.

3) Построение моделирующей программы на специальном языке ИМ или общем языке программирования.

4) Проигрывание различных возможных ситуаций на модели.

5) Верификация модели и программы на основе анализа полученных результатов и их сравнения с теорией процесса и (или) информацией о функционировании реального объекта.

ИМ следует рассматривать как статистический эксперимент, а его результаты представляют собой наблюдения. Любое утверждение относительно характеристик изучаемой системы является статистической гипотезой.

ИМ, по сравнению с обычными методами решения задач исследования операций является более гибким инструментом, особенно в части детализации поведения сложных систем.

Метод Монте-Карло (МК)

ИМ можно считать развитием метода МК, разработанного в 50-х годах прошлого века. Основная идея этого метода состоит в использовании выборок для получения оценок искомых характеристик изучаемых объектов. Задача, при этом, формулируется таким образом, чтобы алгоритм решения использовал случайные числа соответствующих законов распределения. Оказалось, что можно таким образом формализовать детерминированную задачу (вычисление определенных интегралов, например), чтобы решить ее с помощью выборок случайных чисел. Продемонстрируем это на примере. Пусть требуется найти площадь фигуры, ограниченной заданными линиями.

Пусть плоская фигура g составляет часть фигуры G. На фигуру G брошена случайная точка. Тогда вероятность попадания ее нa фигуру g равна отношению площади g к площади фигуры G: (геометрическая вероятность). Следовательно, если известна площадь , то . Используем этот подход для определения площадей фигур, заданных уравнениями границ.

Пример 1. Найти площадь фигуры, ограниченной линиями .

Построим указанные линии. Из Рис. 1 видно, что фигура, площадь которой необходимо найти полностью попадает в прямоугольник с основанием равным 6 и высотой 4 и площадью .

Рис. 1.

Формируем n случайных точек внутри этого прямоугольника.

. Здесь оператор дает случайное число, равномерно распределенное на интервале . Подсчитаем, какое число таких точек попадет на заданную фигуру при помощи программы

.

Вероятность попадания одной точки на фигуру g приближенно равна (и тем точнее, чем больше n) отношению числа точек попавших на фигуру к полному числу точек. и, тогда искомая площадь . С другой стороны, площадь фигуры равна определенному интегралу 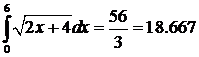. Относительная погрешность метода МК . Повысить точность можно увеличением числа точек или (и) повторением расчета с последующим усреднением.

Пример 2. Найти площадь фигуры, ограниченной линиями 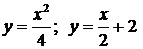. Найдем точки пересечения данных линий и построим график. Из чертежа видно, что фигура, площадь которой необходимо найти полностью попадает в прямоугольник с основанием равным 6 и высотой 4 и площадью .

 

Формируем n случайных точек внутри этого прямоугольника.

. Программа для подсчета, аналогична приведенной и нет необходимости ее приводить.

Вероятность попадания одной точки на фигуру g равна и тогда искомая площадь . Площадь фигуры равна определенному интегралу . Относительная погрешность метода МК в этом примере .

 

Рассмотрим теперь Марковский случайный процесс, протекающий в системе.

 

Марковская цепь с непрерывным временем

 

Имеется некоторая система с k состояниями. Переходы между состояниями происходят мгновенно в случайные моменты времени. Вероятности переходов из любого состояния Si в любое другое Sj являются функциями от времени pij(t). Если случайный процесс, протекающий в системе, обладает свойством отсутствия последействия, то говорят, что задана Марковская цепь с непрерывным временем [2]. Интенсивностью перехода из состояния Si в состояние Sj называется предел , где -вероятность перехода на интервале времени .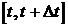

Рассмотрим, для примера, Марковскую цепь с тремя состояниями. Пусть задана матрица интенсивностей переходов и начальное распределение вероятностей состояний

,

Составим размеченный граф состояний этой Марковской цепи (Рис. 3). Очевидно, что данная цепь регулярна и имеет финальное распределение вероятностей состояний, совпадающее со стационарным распределением.

2. Найти стационарное распределение вероятностей состояний.

3. Выполнить моделирование системы и сравнить полученные результаты моделирования с результатами, полученными в пункте 2.

Решение.

1. Составим граф состояний.

 

 

2

S2

S1

3

 

3 1 4 4

	S3

 

 

 

Рис. 3.

По графу видно, что все состояния системы существенны и связаны между собой, поэтому цепь регулярна [2].

Запишем уравнения для вероятностей состояний.

Потоком вероятности из состояния в состояние называют произведение интенсивности этого перехода на вероятность состояния . Производная вероятности состояния будет равна сумме потоков «втекающих» в это состояние без потоков «вытекающих» из него. Тогда, например, для состояния можно записать по графу

или . Записывая по аналогии уравнения для других состояний, получим систему дифференциальных уравнений (Колмогорова).

.

При достижении стационарного состояния вероятности станут постоянными величинами и их производные будут равны нулю. Тогда из системы

совместно с очевидным условием ,

найдем стационарное распределение вероятностей состояний

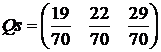
Моделирование процесса, протекающего в данной системе.

Введем переменный массив sj, элементы которого – суммарное время пребывания системы в данном состоянии j, время моделирования ;матрицу В – индикатор состояний (каждый столбец соответствует одному состоянию). Например, при выборе столбца 3 система находится в состоянии 2. Напомним, что в этом разделе элементы массивов нумеруются так 0,1,2,…

; .

 

 

Моделирующая программа.

 

 

Рассмотрим операторы программы по порядку. Задается начальное значение модельного времени t. Вводится матрица iw соответствующая начальному состоянию системы по индикатору состояний и строится цикл while до достижения времени моделирования tm. Определяется номер состояния k, в котором система находится в текущий момент времени. В цикле вычисляем все времена , через которые система может перейти в другое состояние. Находим минимальное из этих времен . Так как цепь Марковская, то она удовлетворяет условию отсутствия последействия, и случайные времена между переходами распределены по показательному закону. Они могут быть найдены с помощью оператора 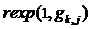. Здесь1показывает, что вычисляется одно значение, а − интенсивность соответствующего перехода. Полученное время суммируется с временем, которое система провела в текущем состоянии s. Определяется номер ind состояния, в которое переходит система, и этот номер учитывается в индикаторе В. Отношения времени пребывания в каждом состоянии к полному времени моделирования, принимаются за оценки стационарных вероятностей состояний . Для рассмотренного примера и времени моделирования получим

 

.

 

Сравнивая результаты моделирования при различных прогонах с различными числами шагов и точные значения стационарных вероятностей состояний, делаем вывод о хорошей сходимости результатов.

Рассмотрим имитационную модель системы массового обслуживания.

 

Одноканальная СМО с неограниченной очередью

Из СМО с ожиданием самой простой является одноканальная СМО с неограниченной очередью. Такие СМО часто встречаются в практике: врач, обслуживающий пациентов; телефон-автомат с одной будкой; ЭВМ, выполняющая заказы пользователей.

Пусть имеется одноканальная СМО с очередью, на которую не наложено никаких ограничений. На эту СМО поступает поток заявок с интенсивностью ; поток обслуживания простейший и имеет интенсивность , .

Найти предельные вероятности состояний СМО, а также характеристики эффективности ее работы.

Запишем состояния СМО (состояния пронумерованы по числу заявок в системе):

канал свободен,

канал занят, очереди нет,

канал занят, одна заявка в очереди,

..................................

канал занят; заявка в очереди,

и так далее.

Теоретически число состояний не ограничено (бесконечно). Граф состояний показан на рисунке 3

 

...

...

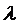
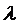
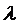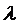
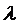
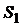
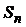
Рис. 3

 

Существуют ли в этом случае предельные вероятности состояний, ведь число состояний системы бесконечно?

Формула для определения имеет вид:

В скобке стоит сумма бесконечной геометрической прогрессии. Если знаменатель прогрессии , то сумму можно вычислить по формуле

Если , то ряд расходится, сумма растет неограниченно, СМО не может работать из-за неограниченно возрастающей очереди. Дальнейшие формулы справедливы только при .

Среднее число заявок в очереди одноканальной СМО и время ожидания обслуживания равно

.

Среднее число занятых каналов - Найдем среднее число заявок в системе:

,

и среднее время нахождения заявки в системе:

.

Пример. На железнодорожную сортировочную горку прибывают составы с интенсивностью состава в час.

Среднее время, в течение которого горка обрабатывает состав, равна 24 минутам. Составы, прибывшие в момент, когда горка занята, становятся в очередь и ожидают в парке прибытия, где имеются три запасных пути, на каждом из которых может ожидать один состав.

Состав, прибывший в момент, когда три запасных пути заняты, ставится на внешний путь. Станция платит штраф за пребывание состава на внешнем пути (а усл. ед. за 1 час). Вычислим вероятности состояний СМО для стационарного случая и коэффициенты эффективности работы горки. Вычислить штраф, который должна выплачивать станция за месяц из-за ожидания обслуживания на внешних путях.

Нас будут интересовать те состояния, при которых составы попадают на внешний путь:

один состав на горке, три в очереди на запасных путях станции, один на внешних путях,

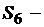один на горке, три на запасных путях, два на внешних путях и так далее.

Вычислим стационарные вероятности состояний СМО:

сост/час; час.; сост./час.

Теперь найдем вероятность того, что прибывающий состав попадает на внешний путь

Таким образом, в 41% случаев состав попадает на внешний путь.

Вычислим коэффициенты эффективности работы горки.

Среднее число составов, ожидающих в очереди (как в парке, так и вне его) -

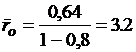состава, часа.

Среднее число составов в парке расформирования -

состава, часа.

Таким образом, составу приходится более 1,5 часов стоять в очереди.

 

Вычислим среднее время ожидания на внешних путях. Составим закон распределения случайной величины ; - число составов, поставленных на внешних путях.

						....
						....

 

В нашем примере:

Вычислим штраф за сутки:

Ш = 2 сост/час. · 24 час. · 0,41 · а = 19,66 а усл.ед.

Решим эту задачу имитационными методами. (Моделирующую программу можно найти в работе [3]).

Результаты для параметров эффективности

 

состава, часа.

Среднее число составов в парке расформирования -

состава, часа. Величина штрафа по результатам моделирования также близка к значению, полученному выше.

 

Все рассмотренные в этой лекции примеры показывают, как можно использовать ИМ для решения самых различных задач. Результаты показывают, что применение классических или моделирующих методов определяется лишь психологическими предпочтениями. Однако, существует большой класс задач прикладного характера, решение которых классическими методами затруднительно или вообще невозможно при современном состоянии развития методов прикладной математики. Рассмотрению таких задач и посвящена следующая лекция.