Далее рассмотрим пример определения параметров сложного трубопровода с использованием характеристик простых трубопроводов.
Сложный трубопровод, схема которого приведена на рисунке 4, включает: распределители 3 и 7, регулируемые дроссели 4 и 6, гидромотор 5, гидроцилиндр 8, фильтр 1, бак 2, а также соединительные гидролинии.

Рисунок 4 – Схема сложного трубопровода
Построить суммарную характеристику сложного трубопровода в координатах p–Q.
При построении принять пределы изменения: давления p от 0 до 12
МПа, расхода Q – от 0 до 1 л/с. Используя полученную характеристику, определить параметры потока в точке К (pК; QК) и скорость перемещения поршня гидроцилиндра 8 при заданной скорости вращения гидромотора 5 ω = 37 рад/с. Все соединительные гидролинии имеют одинаковые диаметры d т = 10 мм и следующие длины:
– от точки K до точки L – l 1 = 6 м;
– от точки L до гидромотора 4 и далее до точки L ′ – l 2 = 3 м;
– от точки L до гидроцилиндра 8 – l 3 = 1,5 м;
–от гидроцилиндра 8 до точки L ′ l 3 = 1,5 м;
–от точки L ′ до бака 5 (точка Т) – l 4 = 4м.
Известны также: момент на валу гидромотора М = 28 Н·м, сила на штоке цилиндра F = 6,5 кН, рабочий объем гидромотора W о = 30 см3, диаметр поршня D = 50 мм, диаметр штока d ш = 30 мм.
Учесть потери в трубопроводах при вязкости жидкости n = 0,75 см2/с
(плотность ρ = 900 кг/м3), а также потери в распределителях 3 и 7 (эквивалентная длина каждого канала l эр = 2 м), в дросселе 4 (коэффициент сопротивления ζ = 30), в дросселе 6 (коэффициент расхода μ = 0,7, проходное сечение S = 18 мм2) и в фильтре 1 (эквивалентная длина l эф = 10 м).
Принять: механический КПД гидромотора – η мм = 0,94, его объемный
КПД – η мо = 0,92, механический КПД гидроцилиндра – η цм = 0,97, а режим течения – ламинарным.
Для облегчения решения схему целесообразно заменить эквивалентной (расчетной). На рисунке 5 представлен один из возможных вариантов эквивалентной схемы, полученной из заданной принципиальной схемы

Рисунок 5 - Эквивалентная схема сложного трубопровода
Сложный трубопровод состоит из четыре простых трубопроводов:
– 1-ый трубопровод от точки К до точки L;
– 2-ой трубопровод от точки L через гидромотор (Гм) до точки L ′ (верхняя ветвь параллельного соединения);
– 3-ий трубопровод от точки L через гидроцилиндр (Гц) до точки L ′
(нижняя ветвь параллельного соединения);
– 4-ый трубопровод от точки L ′ до точки T.
Для каждого из этих простых трубопроводов получим аналитические выражения их характеристик. Для 1-ого простого трубопровода характеристика примет вид

Определим численное значение коэффициента К 1

В результате получим характеристику 1-го трубопровода в виде

Для 2-ого простого трубопровода характеристика примет вид

Определим численные значения постоянных величин



В результате получим характеристику 2-го трубопровода в виде

Для 3-ого простого трубопровода характеристика примет вид:

Определим численные значения постоянных величин

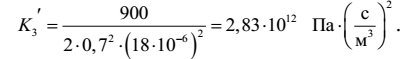
В результате получим характеристику 3-го трубопровода в виде

В результате получим характеристику 4-го трубопровода в виде:

Далее строим графики зависимостей. При этом следует
учитывать, что зависимости (1.26) и (1.29) являются линейными, а зависимости 1.27 и 1.28 носят квадратичный характер. Построение линейных характеристик проводят по двум точкам, а при построении парабол необходимо использовать не менее 5 ¸ 7 точек.
Для удобства необходимые для построения данные целесообразно свести
в таблицу 2.

На рисунке 5 по данным, приведенным в таблице 1.1, построены линии 1, 2, 3 и 4.
Построим суммарную характеристику всего сложного трубопровода. Для этого, прежде всего, следует сложить параллельные трубопроводы 2
и 3. Построенная ломанная линия (2+3) является характеристикой условного
трубопровода (2+3), которым можно заменить параллельное соединение трубопроводов 2 и 3.

Рисунок 5 – Построение характеристики сложного трубопровода и определение параметров его работы
Из преобразованной эквивалентной схемы сложного трубопровода рисунок 6 следует, что он состоит из трех последовательно соединенных простых трубопроводов: 1, (2+3) и 4.

Рисунок 6 - Преобразованная эквивалентная схема сложного трубопровода
Воспользуемся правилами графического сложения характеристик последовательного соединения трубопроводов. В результате получаем суммарную характеристику участков 1, (2+3) и 4 (линия Σ), представленную на рисунке 5.
Она является характеристикой всего сложного трубопровода.
При сложении линейных характеристик следует получить две точки, а при сложении характеристик в виде квадратичных парабол или прямых с параболами необходимо 5 ¸ 7 точек.
Получив суммарную характеристику сложного трубопровода, определим параметры потока в точке К и скорость поршня гидроцилиндра 8.
Для этого необходимо найти рабочую точку на суммарной характеристике, исходя из значений параметров, заданных по условию задачи.
В задаче для этого, по известной величине угловой скорости вращения ω вала гидромотора 5 найдем расход во 2-ом простом трубопроводе Q 2.
Из формулы (1.11) получим

По этой величине расхода во 2-ом трубопроводе Q 2 находим точку на его характеристике (точка R 2 на рисунке 5).
Потом графически определим соответствующую этому режиму точку R ′ на характеристике (2+3) и далее R на характеристике Σ. Последняя
будет являться рабочей точкой для данного сложного трубопровода. Положение точки R на характеристике сложного трубопровода позволяет найти искомые параметры потока в точке К: pК = 9,24 МПа и QК = 0,735·10-3 м3/с.
Для определения скорости перемещения поршня гидроцилиндра 8 найдем рабочую точку на характеристике 3-его трубопровода, в котором установлен гидроцилиндр. Так как 3-ий трубопровод параллелен 2-ому, то эту точку R 3 определим, на той же горизонтали, что и точка R 2.
Величина расхода Q 3 для точки R 3 равна: Q 3 = 0,543·10-3 м3/с.
По величине Q 3, используя формулу (1.15) (принимаем η оц = 1), вычисляем искомую величину скорости поршня

Таким образом, в результате построена суммарная характеристика сложного трубопровода, определены параметры потока в начальной точке этого трубопровода: p К = 9,24 МПа и Q К = 0,735 л/с, а также скорость перемещения поршня гидроцилиндра: V = 43,2 см/с.