Движение математического маятника
В качестве первого примера мы рассмотрим классический пример о движении математического маятника.
Математический маятник (рис. 1) представляет собой тяжелую материальную точку, подвешенную на невесомой и нерастяжимой нити, которая закреплена другим своим концом неподвижно. Совокупность возможных движений мы ограничим условием, что движения маятника плоские.
Рис. 1. Математический маятник.
Введем обозначения: l — длина маятника, φ — угол между нитью и вертикалью, t — время, m — масса груза и N — натяжение нити. Если пренебречь силами сопротивления, то задача о движении маятника приводится к решению уравнений
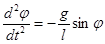, (1)
(2)
с начальным условием
при t=0 φ=φ0 и 
,
т. е. за начальный момент времени принят тот момент, когда маятник отклонен на угол φ0, а скорость равна нулю.
Из уравнений (1), (2) и начального условия очевидно, что в качестве определяющих параметров можно взять следующую систему:
t, l, g, m, φ0.
Числовые значения всех остальных величин определяются полностью значениями этих параметров. Следовательно, мы можем написать
φ = φ (t, φ0, l, g, m), N=mgf(t, φ0, l, g, m) (3)
где φ и f – безразмерные величины.
Числовые значения функций φ и f не должны зависеть от системы единиц измерения. Вид этих функций можно определить либо решая уравнения (1) и (2), либо экспериментальным способом.
Из общих соображений, изложенных выше, вытекает, что пять аргументов функций φ и f можно свести только к двум аргументам, которые представляют собой безразмерные комбинации, составленные из t, l, g, m и φ0, так как имеются три независимые единицы измерения.
Из величин t, l, g, m и φ0 можно составить две независимые безразмерные комбинации
|
|
φ0 и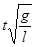 
(4)
Все другие безразмерные комбинации, составленные из t, l, g, m и φ0 или вообще из любых величин, определяемых этими параметрами, будут функциями комбинаций (4). Следовательно, можно написать
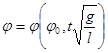, (5')
. (5")
Формулы (5), полученные с помощью метода размерности, показывают, что закон движения не зависит от массы груза, а натяжение нити прямо пропорционально массе груза. Эти выводы вытекают также непосредственно из уравнений (1) и (2). Величину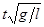 
можно рассматривать как время, выраженное в специальной системе единиц измерения, в которой длина маятника и ускорение силы тяжести приняты равными единице.
Обозначим через Г какой-нибудь характерный промежуток времени, например время движения маятника между крайним и вертикальным положениями или между двумя одинаковыми фазами, т. е. период колебания, и т. д. (существование периодического движения можно принять как гипотезу или как результат, известный из дополнительных данных). Имеем
функция f2 представляет собой безразмерную величину, а так как из l, g и m нельзя составить безразмерную комбинацию, то очевидно, что функция f2 не зависит от l, g и m. Следовательно,
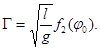(6)
Формула (6) устанавливает зависимость времени Г от длины маятника. Получить вид функции f2(φ0) с помощью теории размерности нельзя. Определение f2(φ0) необходимо произвести либо теоретически, на основании уравнения (1), либо экспериментально.
Формулу (6) можно получить непосредственно из соотношений (5'). В самом деле, для периода колебаний соотношение (5') дает
.
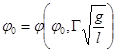Решая это уравнение, получим формулу (6).
|
|
Если Г есть период колебания, то из соображений симметрии очевидно, что период Г не зависит от знака φ0, т. е.
f2(φ0)= f2(-φ0).
Следовательно, функция f2 является четной функцией аргумента φ0. Предполагая, что при малых φ0 функция f2(φ0) регулярна, можно написать
f2(φ0) = c1 + c2φ02 + с3φ04 +… (7)
Для малых колебаний члены со степенями φ02 и выше можно отбросить, и для периода Г мы получаем формулу
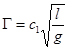. (8)
Решение уравнения (1) показывает, что с1 = 2π. Таким образом, мы видим, что для малых колебаний маятника с помощью теории размерности можно получить формулу периода колебания маятника с точностью до постоянного множителя.
Формулы (5) и (6) сохранят свою справедливость и в том случае, если вместо уравнения (1) мы возьмем уравнение
,
где f(φ) есть любая функция угла φ. Вообще справедливость формул (5) и (6) вытекает из единственного условия, которое состоит в том, что состояние движения определяется параметрами
t, l, g, m, φ0.
Для установления этой системы параметров нам послужили уравнения движения, но ее можно указать и не прибегая к уравнениям движения. В самом деле, для характеристики маятника надо указать l и m. Далее необходимо указать g, так как сущность явления определяется силой тяжести. Наконец, необходимо указать φ0 и t, так как конкретное движение и состояние движения определяются углом крайнего отклонения φ0 и рассматриваемым моментом времени t.