ПРОГРАММИРОВАНИЕ ЛИНЕЙНЫХ АЛГОРИТМОВ
по дисциплине «Основы программирования»
Выполнил: ст-т гр. 19КП2
Сучков А. Ю.
Проверил: доцент каф. ИВС
Хохлов А. Е.
1 Формулировка задачи
С точностью 10-5 вычислить наименьший положительный ненулевой корень уравнения tg x = 2 x, используя метод деления отрезка пополам.
2 Техническое задание
2.1 Требования к программе
Программа должна обеспечивать ввод двух границ, на которых будет вычисляться корень уравнения с заданной точностью путём подстановки в функцию и сужения границ в одну из двух сторон до определённого условия задачи.
2.2 Порядок контроля и приёмки
Для контроля правильности работы программы должен быть разработан тестовый набор данных, состоящий из двух границ. Эти значения надо ввести при работе программы и сравнить с построенным графиком функции.
3 Описание программы
3.1 Общие сведения
Программа разработана в среде Lazarus, её текст приведен в приложении А.
3.2 Функциональное назначение
Программа предназначена для математического вычисления корня уравнения с заданной точностью методом половинного деления.
3.3 Описание логической структуры
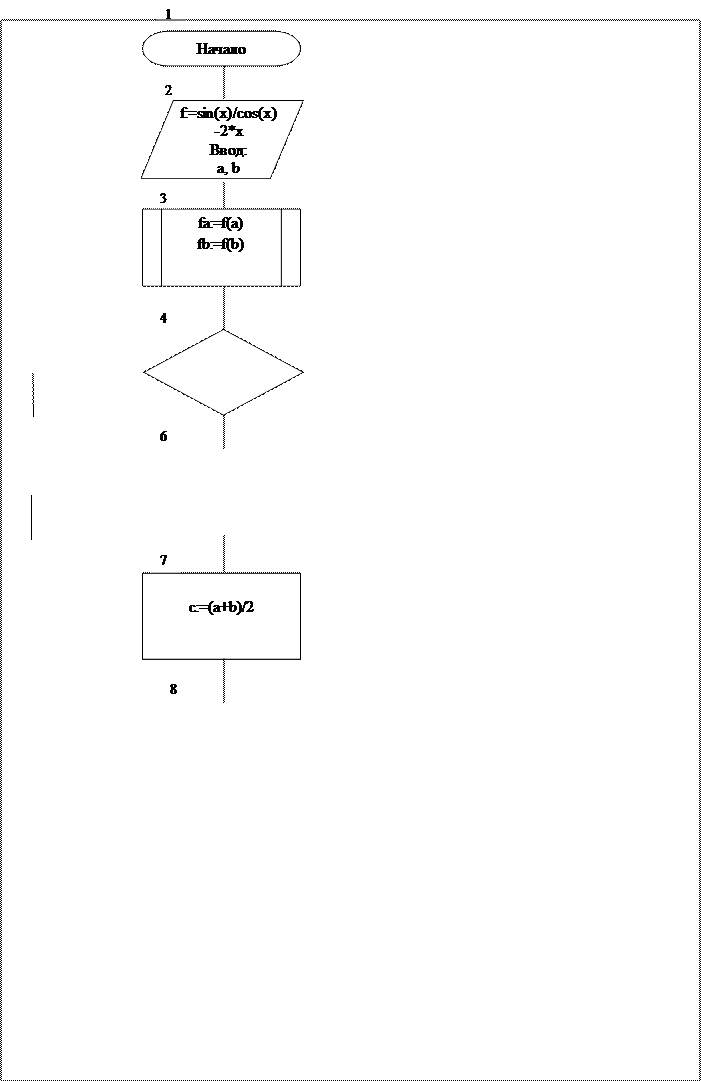
Схема программы представлена на рисунке 1.
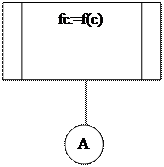
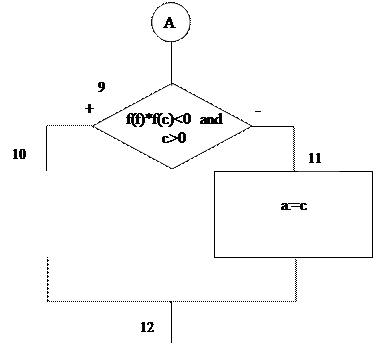
Решение задачи начинается с ввода исходных данных a, b (блок 2). Затем исходные данные присваиваются значению функции (блок 3). Если вводимые числовые значения имеют один и тот же знак, то программа выводит текст “Введены не верные значения для границ” (блок 5) и прекращает свою работу, иначе программа выполняет цикл (блоки 6 - 12). Работы цикла c1 (блок 6) начинается с нахождения среднего значения c для двух границ, заданных условием (блок 4) и вычисления значения функции f в точке с (блок 8). Если произведение значений функций f(a) и f(c) меньше нуля, то в качестве значения c присваивается b, иначе программа присвоит c значение a (блок 7). Цикл c1 будет работать до тех пор, пока не выполнится условие разность b и a по модулю не станет меньше константы e.
Результатом работы программ является нахождение значения x (блок 13) и его вывод на экран (блок 14).
+
|
|
|
 | |||||||
 | |||||||
 | |||||||
 |
|
 |
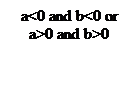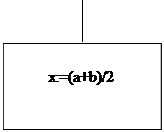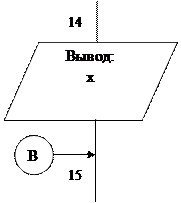Рисунок 1 – Схема программы
 |
Текст программы приведен в приложении А.
На форме расположены следующие объекты:
- три текстовых поля Label1, Label2, Label3 с вкладки Standart. В свойстве Caption этих объектов помещены пояснения для пользователя программы:
Label1.Caption – 'Введите a',
Label2.Caption – 'Введите b',
Label3.Caption – 'Корень уравнения'.
- 2 поля редактирования Edit1, Edit2, с вкладки Standart - для ввода исходных данных и 1 поле Edit3 для вывода полученного результата работы программы;
- кнопка Button1 с вкладки Standart для создания обработчика события, который вычисляет корень заданной функции. В свойстве Caption этого объекта помещено пояснение для пользователя программы: Button1.Caption - 'Рассчитать количество информации'.
Обработчик TForm1.Button1Click обрабатывает щелчок по кнопке «Вычмслить». В разделе описания переменных этого обработчика описаны:
- переменные вещественного типа real:
a – первая граница,
b – вторая граница,
fa – значение функции для a,
fb – значение функции для b,
c – среднее значение,
fc – значение функции для c,
x – корень уравнения,
- раздел const:
e – задаваемая точность.
Исполняемая часть обработчика начинается с ввода исходных данных a, b. Эти переменные вводится с помощью свойства Text объектов Edit. При этом используется стандартная функция преобразования из строкового типа (string) в вещественный тип (real) — StrToFloat. Затем происходит расчет значений для fa, fb подстановкой в функцию и получение среднего значения для c задаваемых границ a, b
f(a):=sin(a)/cos(a)-2*a,
f(b):=sin(b)/cos(b)-2*b,
c:=(a+b)/2
Переход к отношению синуса к косинусу необходим потому, что в языке Object Pascal нет стандартной функции тангенса.
Для вывода результата формируется поле Edit3, в которое записывается результат работы программы преобразования вещественного числа в строку FloatToStrF(x).
4 Программа и методика испытаний
Для проверки правильности работы программы подготовлен тестовый набор данных, представленный в таблице 1 и рисунок 1.
Таблица 1
| Данные | Значение |
| Граница a | -1,5 |
| Граница b |
Вручную рассчитаем функцию для a, b
f(a)=sin(-1,5)/cos(-1,5)-2*(-1,5)=-11,1014199
f(b)=sin(1)/cos(1)-2*(1)=-0,44259227
и среднее значение
c=(-1,5+1)/2=0,25
Рассчитаем значение для функции c
f(c)=sin(0,25)/cos(0,25)-2*(0,25)=0,244685
Приблизительный ответ после ручных расчётов составляет -4.0E-6
Для проверки правильности работы программы необходимо запустить ее на выполнение и ввести исходные данные из таблицы 1. После этого нажать левой кнопкой мыши на кнопку «Вычислить». На форме появляется результат работы программы.
Таблица 2
| Данные | Значение |
| Граница a | -1 |
| Граница b | 1,5 |
Вручную рассчитаем функцию для a, b
f(a)=sin(-1)/cos(-1)-2*(-1)=11,1014199
f(b)=sin(1,5)/cos(1,5)-2*(1,5)=-0,44259227
и среднее значение
c=(1,5+1)/2=2,5
Рассчитаем значение для функции c
f(c)=sin(2,5)/cos(2,5)-2*(2,5)=0,498255
Приблизительный ответ после ручных расчётов составляет 3.8E-6
При работе программы с тестовыми данными получены результаты, приведенные в приложении Б на рисунках Б.1. Результаты приведенные в таблице 2 совпадают с результатами на рисунке Б.1. Таким образом, можно сделать вывод, что программа работает правильно
Если ввести границы a и b, имеющие одинаковые знаки, то программа выведет текстовое сообщение в открывшемся окне и закончит свою работу (см. Рисунок 3).
5 Описание применения
После запуска программы на выполнение на экране появляется 2 строчки для ввода a и b границ (см. Приложение Б). Пользователь должен заполнить поля «Введите a», «Введите b» и нажать левой кнопкой мыши на кнопку «Вычислить». На форме появляется результат работы программы.
Вывод
В ходе выполнения лабораторной работы было сформулировано и утверждено техническое задание на разработку программы, вычисляющей корень уравнения с заданной точностью в сообщении, разработан алгоритм решения 
задачи, составлена и отлажена программа, оформлена документация на программу. Проведенные испытания показали, что программа работает правильно.
 |
ТЕКСТ ПРОГРАММЫ
Приложение А
(обязательное)
unit Unit1;
{$mode objfpc}{$H+}
interface
uses
Classes, SysUtils, FileUtil, Forms, Controls, Graphics, Dialogs, StdCtrls;
type
{ TForm1 }
TForm1 = class(TForm)
Button1: TButton;
Edit1: TEdit;
Edit2: TEdit;
Edit3: TEdit;
Label1: TLabel;
Label2: TLabel;
Label3: TLabel;
procedure Button1Click(Sender: TObject);
private
{ private declarations }
public
{ public declarations }
end;
var
Form1: TForm1;
implementation
{$R *.lfm}
{ TForm1 }
procedure TForm1.Button1Click(Sender: TObject);
function f(x:real):real;
begin
f:=sin(x)/cos(x)-2*x;
end;
const e= 0.00005;
var a,b,c,x,fa,fb,fc:real;
begin
a:=StrToFloat(edit1.text);
b:=StrToFloat(edit2.text);
fa:=f(a);
fb:=f(b);
If (a<0) and (b<0) or (a>0) and (b>0) then
Begin
Edit3.text:=' ';
ShowMessage ('Введены не верные значения для границ')
end
else
Begin
repeat
c:=(a+b)/2;
fc:=f(c);
if (f(a)*f(c)<0) and (c>0) then b:=c
else a:=c;
until abs(b-a)<e;
x:=(a+b)/2;
edit3.text:=FloatToStr(x);
end;
end;
end.
 |
РЕЗУЛЬТАТЫИСПЫТАНИЙ
Приложение Б
(обязательное)
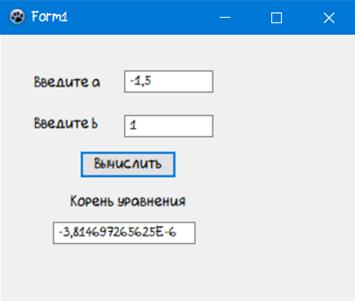
Рисунок Б.1
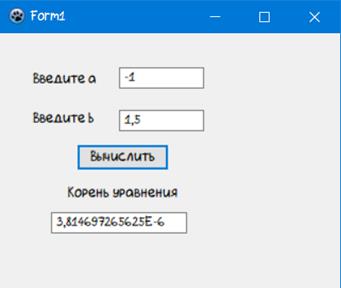
Рисунок Б.2
Рисунок Б.3
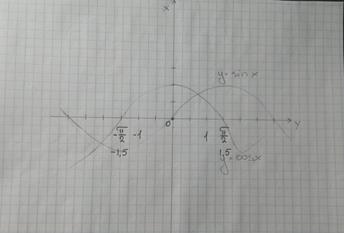
Рисунок Б.4