 Применим II правило Кирхгофа:
Применим II правило Кирхгофа:  . Из определения электроемкости
. Из определения электроемкости  следует, что
следует, что 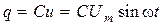 . Учитывая определение силы тока
. Учитывая определение силы тока  получим зависимость мгновенного значения силы тока от времени:
получим зависимость мгновенного значения силы тока от времени:
 , или
, или 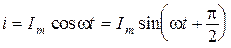 . Следовательно,
. Следовательно,
 ,
,  .
.
Формулу  можно записать в виде
можно записать в виде
 ,
,
 который можно интерпретировать как закон Ома для участка цепи с электроемкостью. Здесь
который можно интерпретировать как закон Ома для участка цепи с электроемкостью. Здесь  представляет емкостное сопротивление.
представляет емкостное сопротивление.
Условие  означает, что синусоиды, изображающие зависимости силы тока и напряжения от времени, сдвинуты относительно друг друга на четверть периода, то есть ток по фазе опережает напряжение на
означает, что синусоиды, изображающие зависимости силы тока и напряжения от времени, сдвинуты относительно друг друга на четверть периода, то есть ток по фазе опережает напряжение на  .
.
Зависимость тока и напряжения на конденсаторе изображены на графике.
Контур с индуктивностью
 При протекании по катушке переменного тока в ней возникает ЭДС самоиндукции
При протекании по катушке переменного тока в ней возникает ЭДС самоиндукции  Применим II правило Кирхгофа:
Применим II правило Кирхгофа:  , или
, или  . Из этого выражения следует, что
. Из этого выражения следует, что
 .
.
Интегрируя это уравнение, получим зависимость мгновенного значения силы тока от времени:
 , или
, или 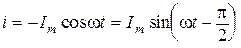 . Следовательно,
. Следовательно,
 ,
,  .
.
Формулу  можно записать в виде
можно записать в виде
 ,
,
который можно интерпретировать как закон Ома для участка цепи с индуктивностью. Здесь  представляет индуктивное сопротивление.
представляет индуктивное сопротивление.
 Условие
Условие  означает, что синусоиды, изображающие зависимости силы тока и напряжения от времени, сдвинуты относительно друг друга на четверть периода, то есть напряжение по фазе опережает ток на
означает, что синусоиды, изображающие зависимости силы тока и напряжения от времени, сдвинуты относительно друг друга на четверть периода, то есть напряжение по фазе опережает ток на  .
.
Зависимость тока и напряжения на индуктивности изображены на графике.
Емкостное и индуктивные сопротивления называют реактивными, сопротивление R - активным сопротивлением.
Реактивное сопротивление измеряют в тех же единицах, что и активное. Но между ними существует и принципиальное различие, а именно: только активное сопротивление определяет необратимые процессы в цепи, такие например, как преобразование электромагнитной энергии в джоулеву теплоту.
Последовательное соединение R, L, C в цепи переменного тока. Закон Ома
 |
При последовательном соединении токи, протекающие по всем элементам цепи, одинаковы, а мгновенные значения напряжений складываются, то есть
 .
.
Таким образом, в результате сложения трех колебаний получается четвертое.
Для сложения колебаний применим метод векторных диаграмм. Вы разим амплитудные значения напряжений на участках цепи через амплитудные значения силы тока:
 ,
, 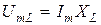 ,
,  . (1)
. (1)
Выделим направление и обозначим его как ось токов. Поскольку сдвиг фаз между током и напряжением на активном сопротивлении равен нулю, вектор напряжения длиной, равной амплитуде  , направим по оси токов. Учитывая, что на индуктивном сопротивлении напряжение опережает ток на
, направим по оси токов. Учитывая, что на индуктивном сопротивлении напряжение опережает ток на  , вектор
, вектор 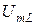 направим перпендикулярно оси токов вверх (будем считать положительными углы поворота против часовой стрелки). Тогда вектор, изображающий напряжение на емкости
направим перпендикулярно оси токов вверх (будем считать положительными углы поворота против часовой стрелки). Тогда вектор, изображающий напряжение на емкости  , которое отстает от тока на
, которое отстает от тока на  , будет ориентирован противоположно вектору
, будет ориентирован противоположно вектору 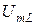 . Результатом сложения этих трех векторов будет вектор длиной
. Результатом сложения этих трех векторов будет вектор длиной  .
.
 Вначале сложим противоположно направленные векторы
Вначале сложим противоположно направленные векторы 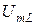 и
и  . Затем применим теорему Пифагора, согласно которой
. Затем применим теорему Пифагора, согласно которой
 .
.
Подставим в эту формулу выражения (1)
 ,
,
откуда выразим амплитуду силы тока
 .
.
Эту формулу можно записать в виде
 ,
,
она представляет закон Ома для участка цепи, содержащего последовательно соединенные активное, емкостное и индуктивное сопротивления. Величину
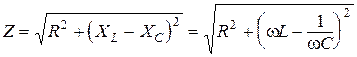
называют полным сопротивлением цепи переменного тока или импедансом.
С помощью векторной диаграммы найдем сдвиг фаз между током и напряжением:
 .
.
В практике широко применяют так называемый коэффициент мощности, равный  . Из векторной диаграммы видно, что
. Из векторной диаграммы видно, что  . Применяя закон Ома, получаем, что
. Применяя закон Ома, получаем, что  , или
, или
 .
.
 В рассматриваемой цепи ток будет максимальным, если
В рассматриваемой цепи ток будет максимальным, если  , то есть напряжения на индуктивном и емкостном сопротивлениях совпадают по величине:
, то есть напряжения на индуктивном и емкостном сопротивлениях совпадают по величине:  . Это явление называется резонансом напряжений.
. Это явление называется резонансом напряжений.
При резонансе полное сопротивление цепи минимально и равно активному сопротивлению: Z = R, сдвиг фаз между током и напряжением равен нулю.
Параллельное соединение R, L, C в цепи переменного тока
 При параллельном соединении напряжения на всех элементах цепи, одинаковы и равны внешнему напряжению, а мгновенные значения токов складываются, то есть
При параллельном соединении напряжения на всех элементах цепи, одинаковы и равны внешнему напряжению, а мгновенные значения токов складываются, то есть
 .
.
Таким образом, в результате сложения трех колебаний получается четвертое.
Также, как и раньше, для сложения колебаний применим метод векторных диаграмм. По закону Ома для участков цепи имеем
 ,
,  ,
,  . (1)
. (1)
Выделим направление и обозначим его как ось напряжений. Поскольку сдвиг фаз между током и напряжением на активном сопротивлении равен нулю, вектор тока длиной, равной амплитуде  , направим по оси напряжений. Учитывая, что на индуктивном сопротивлении напряжение опережает ток на
, направим по оси напряжений. Учитывая, что на индуктивном сопротивлении напряжение опережает ток на  , вектор
, вектор  направим перпендикулярно оси токов вниз. Тогда вектор, изображающий ток на электроемкости
направим перпендикулярно оси токов вниз. Тогда вектор, изображающий ток на электроемкости  , который опережает напряжение на
, который опережает напряжение на  , будет ориентирован противоположно вектору
, будет ориентирован противоположно вектору  . Результатом сложения этих трех векторов будет вектор длиной
. Результатом сложения этих трех векторов будет вектор длиной  .
.
 Вначале сложим противоположно направленные векторы
Вначале сложим противоположно направленные векторы  и
и  . Затем применим теорему Пифагора, согласно которой
. Затем применим теорему Пифагора, согласно которой
 .
.
Подставим в эту формулу выражения (1)
 ,
,
откуда выразим амплитуду напряжения
 .
.
Эту формулу можно записать в виде
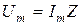 ,
,
она представляет закон Ома для участка цепи, содержащего параллельно соединенные активное, емкостное и индуктивное сопротивления. Величину

называют полным сопротивлением цепи переменного тока или импедансом.
Из векторной диаграммы видно, что при выполнении условия  , или, что то же самое,
, или, что то же самое,  полное сопротивление цепи минимально и равно активному сопротивлению: Z = R. Токи на индуктивном и емкостном сопротивлениях совпадают по величине:
полное сопротивление цепи минимально и равно активному сопротивлению: Z = R. Токи на индуктивном и емкостном сопротивлениях совпадают по величине:  , сдвиг фаз между током и напряжением равен нулю. Это явление называется резонансом токов
, сдвиг фаз между током и напряжением равен нулю. Это явление называется резонансом токов
Комбинированное соединение R, L, C в цепи переменного тока
Фактически “чистых” индуктивностей в природе не существует, любая катушка индуктивности обладает омическим (активным) сопротивлением. Поэтому катушку можно рассматривать как последовательно соединенные индуктивность и активное сопротивление. Рассмотренный выше случай предполагает малость активного сопротивления катушки по сравнению с ее индуктивным сопротивлением.
 Рассмотрим параллельное соединение катушки и конденсатора. При параллельном соединении напряжения на всех элементах цепи, одинаковы и равны внешнему напряжению, а мгновенные значения токов складываются, то есть
Рассмотрим параллельное соединение катушки и конденсатора. При параллельном соединении напряжения на всех элементах цепи, одинаковы и равны внешнему напряжению, а мгновенные значения токов складываются, то есть
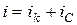 .
.
Связь между амплитудными значениями тока и напряжения на катушке выражается законом Ома
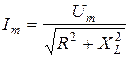 ,
,
а сдвиг фаз между током и напряжением соотношением

 ,
,
причем напряжение опережает ток.
Построим векторную диаграмму для параллельного соединения катушки и конденсатора. Как и раньше, выберем ось напряжений и построим векторы токов  и
и  . Сложим эти векторы по правилу параллелограмма. Силу тока в подводящих проводах
. Сложим эти векторы по правилу параллелограмма. Силу тока в подводящих проводах 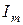 найдем по теореме косинусов
найдем по теореме косинусов
 .
.