В настоящее время в естествознании и в теории управления господствует пространственно временная парадигма (ведущее научное управление). Типичным представителем в теории управления этой парадигмы является критерий оптимального быстродействия. Однако в последние годы в современной прикладной теории управления актуализируется выдвижение синергетической концепции синтеза управляемых систем, базирующейся на теории самоорганизующихся систем.
Синергетика - наука о коллективном, когерентном поведении динамических систем различной природы (от древнегреческого слова “синергос” - вместе действующий), основой которой являются общие закономерности процессов самоорганизации. Самоорганизация - это такой процесс в динамических системах, который приводит вдали от состояния равновесия к возникновению внутренних упорядоченных пространственных и пространственно-временных структур, получивших название диссипативных (от dissipato - рассеивать). Возникновение последних обусловлено обменом энергией, информацией и веществом между элементами системы, внешней средой и их взаимодействием. Образование таких структур приводит к принципиально новым явлениям в поведении системы, а именно к высокой степени упорядоченности поведения огромного количества частиц и вообще компонентов, входящих в состав общей системы.
Примерами процессов самоорганизации являются:
- когерентные колебания в лазерах,
- явления флаттера в авиации,
- образование макроскопических колебательных структур в химии,
- динамика популяций и эволюция как образование макроскопических структур в биологии,
- торнадо и тайфуны - в природе.
В теории управления техническими объектами понятие “диссипативные упорядоченные структуры” оказывается весьма полезным, поскольку позволяет изучать динамические свойства систем с единых математических позиций и единых понятий.
|
|
Диссипативные структуры, на которых могут возникать когерентные или хаотические колебания, получили названия аттракторов. Если рассматривать состояние и движение системы в фазовом пространстве, то аттрактор - это притягивающее множество, то есть некоторая совокупность точек, к которой притягиваются все близлежащие траектории движения.
В фазовом пространстве линейных и нелинейных динамических систем существуют различные типы аттракторов: точка (в частности, устойчивый фокус), устойчивый узел, предельный цикл, тор и “странный аттрактор”.
Обычный аттрактор определяет установившийся режим движения системы, к нему устремляются все переходные режимы, попавшие в область его притяжения. Этот класс аттракторов отличается тем, что они всегда лежат на многообразиях в пространстве состояний системы и называются притягивающими.
Притягивающие многообразия, остающиеся неизменными, называются инвариантными. Движение ИТ вдоль инвариантного аттрактора существенно отличается от движения ее, когда она находится вне аттрактора.
Пример 2:
Рассмотрим механическую систему: пружина (1) - груз существенной массы М (2) - демпфер (3). (рис.2).
 |
1
 |
2
3
 | |||
| |||
 |
Рис.2. Механическая система
В статике 
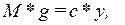где с - коэффициент жесткости пружины, g - ускорение свободного падения 9,81 м/сек2, y – величина растяжения пружины. Таким образом, в статике сила гравитации (левая часть уравнения), уравновешивается силой растяжения пружины (правая часть уравнения).
|
|
Дифференциальное уравнение движения этой системы из некоторого начального состояния 
имеет вид:
(1)
где a - коэффициент демпфирования демпфера.
Если ввести обозначение y - Zo = x, то уравнение (1) можно привести к виду:
, (2)
где 2 h = а/M, w2= c/M.
Характеристическое уравнение (2)
,
а его корни 
.
В таких системах всегда h > w поэтому корни характеристического уравнения - вещественные и разные. Обозначим х через x1 и представим уравнение (2) в виде системы двух уравнений:
. (3)
Поделив первое уравнение на второе, получим уравнение фазовых траекторий
. (4)
Уравнение (4) решается подстановкой 
/ 
. Тогда:
Все фазовые траектории стягиваются к началу координат. Можно, однако, показать, что существуют два луча, проходящих через начало координат, которые одновременно являются фазовыми траекториями. Уравнение лучей:
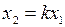. (4а)
Отсюда
, 
. (5)
Тогда с учетом уравнения (4) можно записать:
,
, (6)
, 
, (5.6а)
где k1, k2 - корни уравнения (6), которые одновременно являются корнями характеристического уравнения (2), а уравнение (5) - решением уравнения (5.2). Это свидетельствует о том, что луч x2 =k x1 существует и что этих лучей два. Они располагаются соответственно во втором и четвертом квадрантах фазовой плоскости. Линия x2 =kx1 есть инвариантный аттрактор (притягивающее многообразие). Его уравнение
y(x1,x2) = x2 - k x1 = 0 (7)
есть аттрактор типа «устойчивый узел». Движение изображающей точки на фазовой плоскости вдоль аттрактора описывается дифференциальным уравнением
|
|
,
порядок которого на единицу меньше исходного дифференциального уравнения. Его решение
,
. (8)
Из уравнения (8) видно, что движение вдоль инвариантного многообразия описывается уравнением, существенно отличающимся от исходного (2).