Задание.
- Переписать текст задачи, заменяя все параметры их значениями для решаемого варианта.
- Определить исследуемое событие А и другие события.
- Установить, какие формулы следует использовать для вычислений и выполнить их.
- Номер варианта = порядковый номер в списке группы.
Задача 1. Бросаются две монеты. Найти вероятность того, что:
1) на обеих монетах появиться «герб»,
2) хотя бы на одной монете появиться «герб»,
3) ни на одной монете не появиться «герб»;
Бросаются три монеты. Найти вероятность того, что:
4) на всех монетах появиться «герб»,
5) хотя бы на одной монете появиться «герб»,
6) только на двух монетах появиться «герб»,
7) только на одной монете появиться «герб»,
8) ни на одной монете не появиться «герб»;
Бросаются четыре монеты. Найти вероятность того, что:
9) на всех монетах появиться «герб»,
10) хотя бы на одной монете появиться «герб»,
11) только на одной монете появиться «герб»,
12) только на двух монетах появиться «герб»,
13) только на трех монетах появиться «герб»,
14) ни на одной монете не появиться «герб»;
Бросают игральную кость. Найти вероятность того, что на верхней грани появится:
15) четное число очков,
16) «1» или «6».
Бросают две игральные кости. Найти вероятность того, что на верхних гранях появятся следующие числа очков:
17) только четные,
18) одно четное, другое нечетное,
19) сумма которых четна,
20) сумма которых нечетна,
21) сумма которых больше, чем их произведение,
22) сумма которых меньше шести,
23) сумма которых больше восьми;
Бросают три игральные кости. Найти вероятность того, что на верхних гранях появятся следующие числа очков:
24) 24) только четные,
25) одно четное, другое нечетное,
26) сумма которых четна,
27) сумма которых нечетна,
28) которые все одинаковы,
29) которые все различны,
30) сумма которых делится на четыре.
Задача 2. Слово составлено из карточек, на каждой из которых написана одна буква. Затем карточки смешивают и вынимают без возврата по одной. Найти вероятность того, что буквы вынимаются в порядке заданного слова, если заданным словом является ваша фамилия.
Задача 3. В урне содержится K черных и H белых шаров, Случайным образом вынимают M шаров. Найти вероятность того, что среди них имеется:
а) P белых шаров;
б) меньше, чем P белых шаров;
в) хотя бы один белый шар.
Значения параметров K, H, M и P по вариантам:
| № | |||||||||||||||
| K | |||||||||||||||
| H | |||||||||||||||
| M | |||||||||||||||
| P |
| № | |||||||||||||||
| K | |||||||||||||||
| H | |||||||||||||||
| M | |||||||||||||||
| P |
Задача 4. Устройство состоит из трех независимых элементов, работающих в течении времени t безотказно соответственно с вероятностями p1, p2 и p3. Найти вероятность того, что за время t выйдет из строя:
1) только один элемент;
2) хотя бы один элемент.
Значения параметров вычислить по формулам:
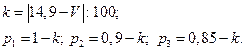
где V – номер варианта.
Задача 5. В первой урне K белых и L черных шаров, а во второй урне M белых и N черных шаров. Из первой урны вынимают случайным образом P шаров, а из второй – Q шаров. Найти вероятность того, что среди вынутых шаров:
1) все шары одного цвета;
2) Только три белых шара;
3) Хотя бы один белый шар.
Значения параметров K, L, M, N, P и Q по вариантам:
| № | |||||||||||||||
| K | |||||||||||||||
| L | |||||||||||||||
| M | |||||||||||||||
| N | |||||||||||||||
| P | |||||||||||||||
| Q |
| № | |||||||||||||||
| K | |||||||||||||||
| L | |||||||||||||||
| M | |||||||||||||||
| N | |||||||||||||||
| P | |||||||||||||||
| Q |
Задача 6. В урне K белых и черных шаров, к ним добавляют L белых шаров. После этого из урны случайным образом вынимают M шаров. Найти вероятность того, что все вынутые шары белые, предполагая, что все возможные предположения о первоначальном содержании урны равновозможны.
Значения параметров K, L и M,по вариантам:
| № | |||||||||||||||
| K | |||||||||||||||
| L | |||||||||||||||
| M |
| № | |||||||||||||||
| K | |||||||||||||||
| L | |||||||||||||||
| M |
Задача 7. В первой урне K белых и L черных шаров, а во второй урне M белых и N черных шаров. Из первой урны вынимают случайным образом P шаров и опускают во вторую урну. После этого из второй урны также случайно вынимают R шаров. Найти вероятность того, что все шары, вынутые из второй урны, белые.
Значения параметров K, L, M, N, P и R по вариантам:
| № | |||||||||||||||
| K | |||||||||||||||
| L | |||||||||||||||
| M | |||||||||||||||
| N | |||||||||||||||
| P | |||||||||||||||
| R |
| № | |||||||||||||||
| K | |||||||||||||||
| L | |||||||||||||||
| M | |||||||||||||||
| N | |||||||||||||||
| P | |||||||||||||||
| R |
Задача 8. В пирамиде стоят R винтовок, из них L с оптическим прицелом. Стрелок, стреляя из винтовки с оптическим прицелом, может поразить мишень с вероятностью p1? А стреляя из винтовки без прицела, – с вероятностью p2. Найти вероятность того, что стрелок поразит мишень, стреляя из случайно взятой винтовки.
Значения параметров вычислить по формулам:
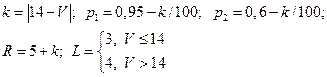
где V – номер варианта.
Задача 9. В монтажном цехе к устройству присоединяется электродвигатель. Электродвигатели поставляются тремя заводами–изготовителями. На складе имеются электродвигатели этих заводов соответственно в количестве M1, M2 и M3 штук, которые могут безотказно работать до конца гарантийного срока с вероятностями соответственно p1, p2 и p3. Рабочий берет случайно один электродвигатель и монтирует его к устройству. Найти вероятности того, что смонтированный и работающий безотказно до конца гарантийного срока электродвигатель поставлен соответственно первым, вторым или третьим заводом–изготовителем.
Значения параметров вычислить по формулам:
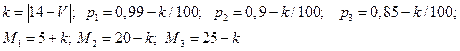
где V – номер варианта.
Задача 10. В каждом из n независимых испытаний событие А происходит с постоянной вероятностью p. Вычислить все вероятности Pn(m). Построить многоугольник распределения и найти наивероятнейшее число появлений события А.
Значения параметров вычислить по формулам:
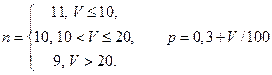
где V – номер варианта.