Лекция. Дифференциальные уравнения второго порядка.
Уравнения, допускающие понижение порядка.
Рассмотрим дифференциальное уравнение вида: y’’= f(x). Дважды интегрируем правую часть и получаем общее решение.
Пример 1
Найти общее решение дифференциального уравнения y’’ = x2 – 2x
Решение:
Данное дифференциальное уравнение имеет вид y’’= f(x). Дважды интегрируем правую часть и получаем общее решение.
Понижаем степень уравнения до первого порядка:
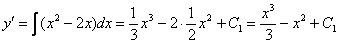
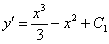, где С1 – константа
Теперь интегрируем правую часть еще раз, получая общее решение:
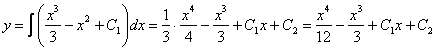
Ответ: общее решение: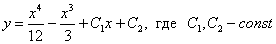 
Проверить общее решение такого уравнения обычно очень легко. В данном случае необходимо лишь найти вторую производную:
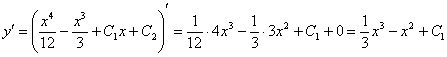
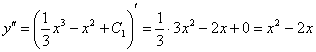
Получено исходное дифференциальное уравнение y’’ = x2 – 2x, значит, общее решение найдено правильно.
2) В дифференциальном уравнении в явном виде отсутствует функция у
Простейшее уравнение данного типа в общем виде выглядит так: F(x, y', y'')=0.
В этом уравнении всё есть, а «игрека» нет. Точнее, его нет в явном виде, но он обязательно всплывёт в ходе решения. Кроме того, во всех этих уравнениях обязательно присутствует независимая переменная «икс».
Решаются такие уравнения с помощью замены.
Пример 2
Решить неполное дифференциальное уравнение второго порядка: y’’= 5x - 1
Решение:
Пусть у’ = u, тогда y’’ = u’, получим u’ = 5x – 1 или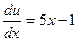 
Разделим переменные: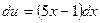 
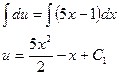
Подставляя обратно в уравнение у’ = u получим:
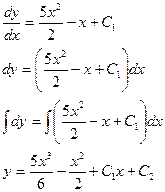
На заключительном этапе нарисовался партизан «игрек», который, как мы помним, в дифференциальное уравнение в явном виде не входил.
Ответ: Общее решение: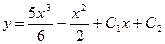 
Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Дифференциальное уравнение вида: у’’+рy’+qy = f(x)
где коэффициенты p, q – постоянные, называется линейным дифференциальным уравнением второго порядка с постоянными коэффициентами
В теории и практике различают два типа таких уравнений – однородное равнение и неоднородное уравнение.
Однородное ДУ второго порядка с постоянными коэффициентами имеет следующий вид:
у’’+рy’+qy = 0, где p и q – константы (числа), а в правой части – строго ноль.
Неоднородное ДУ второго порядка с постоянными коэффициентами имеет вид:
у’’+рy’+qy = f(x), где p и q – константы, а f(x) – функция, зависящая только от «икс». В простейшем случае функция f(x) может быть числом, отличным от нуля.
Чтобы научиться решать неоднородные уравнения необходимо уметь решать однородные уравнения. По этой причине сначала рассмотрим алгоритм решения линейного однородного уравнения второго порядка:
у’’+рy’+qy = 0
Для того чтобы решить данное ДУ, нужно составить так называемое характеристическое уравнение:
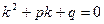или 
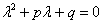
По какому принципу составлено характеристическое уравнение, отчётливо видно:
вместо второй производной записываем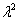 
;
вместо первой производной записываем просто «лямбду»;
вместо функции у ничего не записываем.
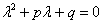– это обычное квадратное уравнение, которое предстоит решить.
В зависимости от значений корней характеристического уравнения записываем общее решение ЛОДУ с постоянными коэффициентами в виде:
1) Характеристическое уравнение имеет два различных действительных корня
Если характеристическое уравнение 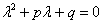имеет два различных действительных корня 
, 
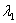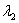(т.е., если дискриминант 
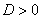), то общее решение однородного уравнения выглядит так:
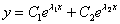, где 
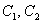– константы.
В случае если один из корней равен нулю, решение очевидным образом упрощается; пусть, например,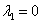 
, тогда общее решение: 
.
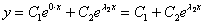2) Характеристическое уравнение имеет два кратных действительных корня
Если характеристическое уравнение 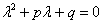имеет два кратных (совпавших) действительных корня 
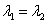(дискриминант D=0), то общее решение однородного уравнения принимает вид: 
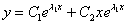, где 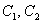– константы.
Вместо 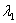в формуле можно было нарисовать 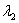, корни всё равно одинаковы.
Если оба корня равны нулю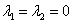 
, то общее решение имеет вид: 
.
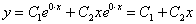Пример 3
Решить дифференциальное уравнение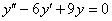 
Решение: составим и решим характеристическое уравнение:
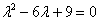
Вычисляя дискриминант, получаем два кратных действительных корня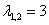 
Ответ: общее решение: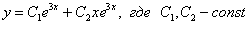 
3) Характеристическое уравнение имеет сопряженные комплексные корни (Данный случай приведен только для ознакомления. Тему «Комплексные числа мы будем проходить позже»)
Если характеристическое уравнение 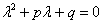имеет сопряженные комплексные корни 
, 
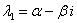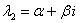(дискриминант 
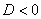), то общее решение однородного уравнения принимает вид:
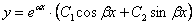, где 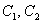– константы.
Примечание: Сопряженные комплексные корни почти всегда записывают кратко следующим образом: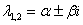 
Если получаются чисто мнимые сопряженные комплексные корни: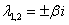 
, то общее решение упрощается:
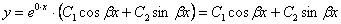
Пример 4
Решить однородное дифференциальное уравнение второго порядка
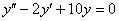
Решение: Составим и решим характеристическое уравнение:
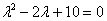
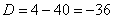
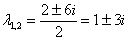– получены сопряженные комплексные корни
Ответ: общее решение: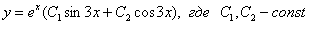 
Дома: 1. Составить конспект лекции;
2. Разобрать примеры из лекции:
3. Решить примеры: Найдите общее решение:
1. у'' + 2у' -35у = 0
2. у'' + 14у' + 49у = 0
3. у'' - 4у' +12у = 0