Прежде всего, изучите разделы 11.1 и 11.2 пособия “Математический анализ” (файл Мат.ан.2013.pdf) – с. 97 - 99.
Все определения, утверждения и доказательства этих разделов приводятся для случая вещественной переменной, но они практически дословно переносятся на случай комплексной переменной. Неравенство вида
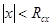на числовой прямой определяет интервал, а на комплексной плоскости – круг радиуса 
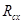, поэтому понятие “интервал сходимости” для случая комплексной переменной превращается в “круг сходимости”.
Итак, перенос изложенного в указанных разделах материала на случай комплексной переменной позволяет получить следующее утверждение.
Областью сходимости степенного ряда от комплексной переменной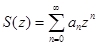 
является круг 
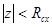, точнее ряд абсолютно сходится во всех точках внутри этого круга и расходится во всех точках вне круга (поведение на границе круга может быть разным).
В частности, возможны крайние случаи, когда область сходимости фактически перестает быть кругом: при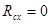 
область сходимости представляет собой единственную точку 
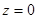, а при 
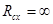- всю комплексную плоскость.
Если записать степенной ряд в более общем виде, подставив вместо переменной z ее разность с фиксированной точкой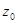 
, то областью сходимости такого ряда 
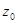будет круг с центром в точке , определяемый неравенством 
.
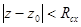Итак, область сходимости степенного ряда определяется единственным числом – его радиусом сходимости 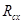. Вычислять радиус сходимости можно по формуле, доказанной в Предложении 11.1 в конце раздела 11.2 пособия. В некоторых случаях более удобно пользоваться другой формулой, основанной на признаке Даламбера. Выведем эту формулу для наиболее общего вида степенного ряда.
Предложение 11.1а. Пусть для степенного ряда существует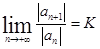 
. Если 
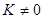, то 
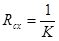(при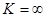 
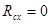); если 
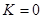, то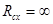 
.
Доказательство. Рассмотрим ряд из модулей общих членов исходного ряда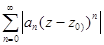 
= 
= 
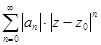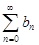и применим к этому ряду признак Даламбера. Для этого вычислим 
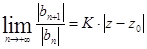. Если K = 0, то этот предел равен 0 при любом z, и по признаку Даламбера исходный ряд абсолютно сходится на всей комплексной плоскости (). Если 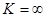, то абсолютной сходимости ряда нет ни при каком z (кроме 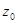), и значит 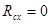. При конечном значении 
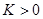по признаку Даламбера ряд абсолютно сходится при 
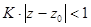, а при 
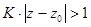абсолютной сходимости нет. Таким образом, круг сходимости ряда определяется неравенством 
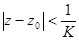, это и значит, что .
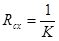Определение. Функция комплексной переменной, которая может быть представлена в виде суммы степенного ряда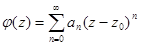 
называется аналитической внутри круга сходимости этого ряда.
Например, любой многочлен является аналитической функцией на всей комплексной плоскости (так как он фактически представляет собой степенной ряд с конечным числом членов, который совпадает со своими частичными суммами с достаточным числом слагаемых, и поэтому везде сходится).
Еще один пример – функция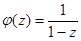 
. Согласно формуле суммы членов бесконечно убывающей геометрической прогрессии при 
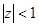справедливо равенство 
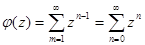, поэтому данная функция является аналитической в круге .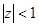