ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
«СИБИРСКИЙ КОЛЛЕДЖ ТРАНСПОРТА И СТРОИТЕЛЬСТВА
Методические указания по выполнению расчетно-графических работ
для студентов обучающихся по специальности:
270835 «Строительство железных дорог, путь и путевое хозяйство»
Практическая работа № 1
Определение равнодействующей плоской системы сходящихся сил
Задания
Заданы модули сил F1, F2, F3, пересекающихся в одной точке, и направление этих сил – углы α1, α2, α3 относительно оси Х
Цель работы – произвести графическое и аналитическое исследование плоской системы сходящихся сил, выявить уравновешена ли заданная система сил.
Задание:
F1 = 4Н, α = 45 
, F2 = 2Н, α2 = 135 , F3 = 5H, α3 = 315
1. Графическое определение равнодействующей.
Выбираем масштаб сил – μF =
Модуль равнодействующей -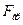 
= μF * 1 = 2,3 H
Направление равнодействующей - 
= 18°
2. Аналитическое определение равнодействующей проекции заданных сил на оси х и у:
F1x = F1* cosα1= 4*cos 135° = -2.828 H; F1y = F1* sin α1 = 4* sin 135° = 2.828 H
F2x = F2 * cosα2 = 2* cos 45° = 1,414 H; F2y = F2 * sin α2 = 2* sin 45° = 1,414H
F3x = F3* cosα3 = 5* cos 315° = 3,535 H; F3y = F3* sin α3 = 5*sin 315° = -3,535 H
Проекции равнодействующей:
F∑x = ∑Fix = -2.828 +1,414 + 3,535 = 2,121 H,
F∑y =∑Fiy = 2.828 + 1.414 – 3,535 = 0,707 H,
Модуль равнодействующей: F∑ah= 
= 2.23 H
Направление равнодействующей: α 
= arctg 
3. Относительные погрешности
Погрешность вычисления модуля равнодействующей.
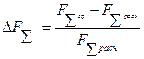* 100% = 
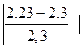х 100% = 3,0%
Погрешность вычисления направления равнодействующей
*100% = 
х100% = 2.3%
|
|
Вывод: система является неуравновешенной.
Модуль равнодействующей - F∑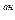 
= 2.23 Н, направление - 
= 18.43°.
Относительные погрешности не превышают 5.0%
Контрольные вопросы
1. Как производится графическое сложение сил, приложенных к твёрдому телу в одной точке?
2. Влияет ли порядок сложения векторов при построении силового многоугольника на величину равнодействующей?
3. Каково направление равнодействующей силы в силовом многоугольнике?
4. Можно ли построив силовой многоугольник, сделать вывод об уравновешенности заданной системы?
5. Как определяется проекция силы на ось? В каком случае она равна нулю?
6. Каково аналитическое условие равновесия плоской системы сходящихся сил?
7. В каких случаях следует графический способ определения равнодействующей, а в каких –
аналитический?
8. Как можно произвести уравновешивание плоской системы сходящихся сил?
Таблица 1.1
| № варианта | Заданные силы, Н | Углы между силой и осью х, град | ||||
| F1 | F2 | F3 | α1 | α2 | α3 | |
Расчетно-графическая работа № 2
|
|
Определение опорных реакции статически определимых балок
Цель работы – построить расчётную схему балки, составить уравнения равновесия балки, определить реакции ее опор и выявить наиболее нагруженную опору.
Задание
Задана горизонтальная двух опорная балка. Балка нагружена активными силами: сосредоточенной F, распределенной силой интенсивностью q и парой сил с моментом М (табл.2.1 и рис 2.6).
Теоретическое обоснование
Во многих машинах и сооружениях встречаются конструктивные элементы, предназначенные преимущественно для восприятия нагрузок, направленных перпендикулярно их оси. Расчетные схемы таких элементов (валы, части металлоконструкции и др.) могут быть представлены балкой. Балки имеют опорные устройства для передачи усилий и сопряжения с другими элементами.
Основными типами опор балок являются шарнирно – подвижная, шарнирно – неподвижная опоры и жесткая заделка.
Шарнирно – подвижная опора (рис.2.1,а) допускает поворот балки вокруг оси шарнира и линейное перемещение на незначительное расстояние параллельно опорной плоскости. Точкой приложения опорной реакции является центр шарнира. Направление реакции R – перпендикуляр к опорной поверхности.
|
|
Шарнирно – неподвижная опора (рис.2.1,6) допускает только поворот балки вокруг оси шарнира. Точкой приложения являются также центр шарнира. Направления реакции здесь неизвестно, оно зависит от нагрузки, приложенной к балке. Поэтому для такой опоры определяются две неизвестные – взаимно перпендикулярные составляющие Rx и Ry опорной реакции.
Жесткая заделка (защемление) (рис.2.1,в) не допускает ни линейных перемещений, ни поворота. Неизвестными в данном случае являются не только величина, но и её точка приложения. Таким образом, для определения опорной реакции необходимо найти три неизвестные: составляющие Rx и Ry по осям координат и реактивный момент MR относительно центра тяжести опорного сечения балки.
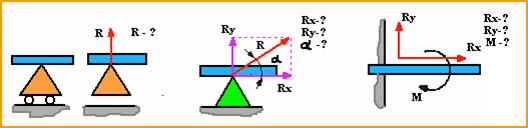
А б в
Рис.2.1
Равновесие балки под действием любой системы заданных сил, расположенных в одной плоскости, может быть обеспечено одной жёсткой заделкой или двумя опорами – подвижной и неподвижной. Балки называются соответственно консольными (рис.2.2,а) или двух опорными (рис.2.2,б)
А б
Рис.2.2
На балку действуют заданные силы и пары сил. Силы по способу приложения делятся на распределенные и сосредоточенные. Распределенные нагрузки задаются интенсивно q, Н/м и длиной L м, равномерно распределенные нагрузки условно изображаются в виде прямоугольника, в котором параллельные стрелки указывают, в какую сторону действует нагрузка (рис.2.3). В задачах статики равномерно – распределенную нагрузку можно заменять равнодействующей сосредоточенной силой Q, численно равной произведению q*1, приложенной посредине длины и направленной в сторону действия q.
Рис.2.3 Рис. 2.4
Сосредоточенные нагрузки приложены на сравнительно небольшой длине, поэтому считается, что они приложены в точке. Если сосредоточенная сила приложена под углом к балке, то для определения реакции опор удобно разложить её на две составляющие – Fx = F cosα и Fy =F sinα (рис.2.4).
Реакции опор балки определяются из условий равновесия плоской системы произвольно расположенных сил. Для плоской системы можно составить три независимых условия равновесия:
∑Fix = 0; ∑Fiy = 0; ∑Mio = 0 или
∑Мia = 0; ∑MiB = 0; ∑MiC = 0 или 
} (2.1)
∑MiA = 0; ∑MiB = 0; ∑Fix = 0.
Где О, А,В, С – центры моментов.
Рационально выбрать такие уравнения равновесия, в каждое из которых входила бы по одной
неизвестной реакции.