ЧИСЛОВЫЕ РЯДЫ. ОСНОВНЫЕ ПОНЯТИЯ
1. 
- числовой ряд, числа 
- члены ряда.
2. 
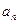- общий член ряда. Нижний индекс 
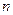- номер члена ряда.
3. Сумма 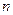первых членов ряда 
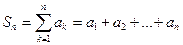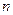- -ая частичная сумма ряда.
4. 
- сумма ряда
5. Если 
ряд называется сходящимся. Если же 
или не существует, то ряд называют расходящимся.
6. 
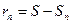- остаток ряда.
Свойства рядов
10. Если у сходящегося ряда отбросить конечное число его членов, то полученный ряд также будет сходящимся.
Верно и обратное утверждение: если сходится ряд, полученный отбрасыванием конечного числа членов у данного ряда, то и данный ряд также сходится.
20. Если 
сходится, и его сумма равна 
, то ряд 
, где 
- произвольное число, также сходится, причем его сумма равна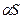 
.
30. Пусть ряды и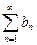 
сходятся, и их суммы, соответственно равны 
и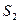 
. Тогда ряд 
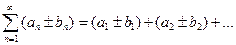также сходится, причем его сумма равна 
.
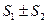Исследование сходимости рядов обычно сводится к вычислению пределов. При этом часто используются известные условия эквивалентности бесконечно малых, которые применительно к рядам при 
принимают вид:
(формула Стирлинга)
Часто приходится иметь дело с пределами:
.
ПРИЗНАКИ СХОДИМОСТИ ЧИСЛОВЫХ РЯДОВ
Необходимый признак сходимости ряда
Если ряд (1) сходится, то его общий член 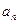стремится к нулю при , т.е. 
.
Следствие: Если 
, то ряд расходится.
Признаки сравнения
Пусть даны два числовых ряда с положительными членами:
(1)
(2)
Первый признак сравнения. Если для некоторого числа 
при всех натуральных 
выполняется неравенство
1) 
и ряд (2) сходится, то ряд (1) тоже сходится;
2) 
и ряд (2) расходится, то ряд (1) тоже расходится.
Второй признак сравнения. Если существует конечный и отличный от нуля предел 
, то ряды (1) и (2) сходятся или расходятся одновременно.
При использовании признаков сравнения исследуемый ряд часто сравнивают
с бесконечной геометрической прогрессий 
,
где а – любой число, отличное от нуля, которая при 
сходится, а при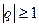 
расходится, или
С рядом Дирихле
, где 
, который при 
сходится, при 
расходится.
При 
этот ряд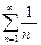 
называется гармоническим рядом.
Признак Даламбера
Пусть для ряда , 
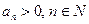существует предел 
. Тогда
1) если 
, то ряд сходится,
2) если 
, то ряд расходится,
3) если 
, то о сходимости или расходимости ряда ничего сказать нельзя и в этом случае нужно применить другой признак сходимости.
Замечание: Признак Даламбера применяют, если общий член ряда содержит показательные функции 
и/или факториалы 
или аналогичные по скорости роста функции.
Признак Коши
Пусть для ряда , 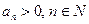существует предел 
. Тогда
1) если , то ряд сходится,
2) если , то ряд расходится,
3) если , то о сходимости или расходимости ряда ничего сказать нельзя и в этом случае нужно применить другой признак сходимости.
Замечание: Признак Коши используется, если общий член ряда содержит , 
или аналогичные по скорости роста функции.
Интегральный признак Коши-Маклорена
Если функция 
на промежутке 
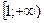является непрерывной, положительной и невозрастающей, то числовой ряд , где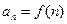 
сходится или расходится одновременно с интегралом 
.
Замечание 1. Нижним пределом интегрирования может быть любое другое положительное число из области определения функции.
Замечание 2. С помощью интегрального признака легко доказать, что ряд Дирихле сходится при и расходится при .
Признак Лейбница
Если члены знакочередующегося ряда 
(
)
1) монотонно убывают по абсолютной величине, то есть 
;
2) и ,
То данный ряд сходится.
Замечание: Если знакочередующийся ряд 
() сходится, то его сумма положительна и не превосходит первого члена ряда, то есть 
.
Если знакочередующийся ряд начинается с отрицательного члена
(), и для него выполнены условия признака Лейбница, то он сходится и его сумма отрицательна и удовлетворяет неравенству 
.
Следствие: При замене суммы ряда, удовлетворяющего признаку Лейбница, суммой 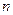его первых членов 
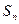абсолютная величина ошибки 
не превышает абсолютного значения первого из отброшенных членов, то есть 
. Знак ошибки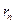 
совпадает со знаком первого из отброшенных членов.