Решение
Способ (традиционный, длинный)
Следите за преобразованиями и вычислениями
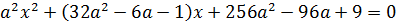
При 
получим 
.
Проверим условие 
Значит, не подходит.
Данное уравнение при 
является квадратным.
Рассмотрим варианты
1. 
При 
Отсюда, при 
.
Проверим условие 
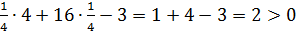, значит, 
подходит.
При 
Проверим условие
, значит, 
не подходит.
2. 
Уравнение будет иметь ровно одно решение тогда и только тогда, когда из этих корней один удовлетворяет условию , а другой нет.
Рассмотрим варианты
1. 
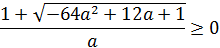
Так как числитель дроби положителен, если корень определён, то неравенство выполнено при положительном знаменателе. Значит, при 
данный корень удовлетворяет условию.
2. 
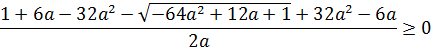
Подумайте, почему система именно такая
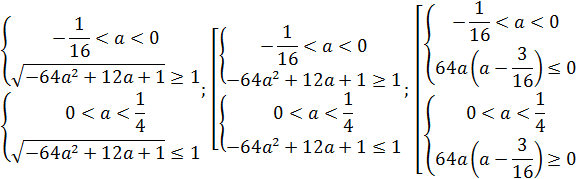
Решением является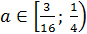 
. Значит, при 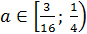данный корень удовлетворяет условию.
Отсюда получаем, что при 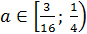оба корня удовлетворяют условию, а при 
только один.
Таким образом, получим, что при 
уравнение имеет единственное решение.
Ответ:
Замечание: данный способ можно слегка упростить, если привлечь графические соображения (как в рассмотренном далее способе 3) – подумайте, как именно
Если вы дочитали внимательно до этого места и со всем разобрались, то, наверное, понятно, что таким способом решать задачу не стоит
способ (замена переменной)
Значит, решение задачи сводится к следующему – при каки значениях 
имеет единственное решение система 
При получим 
. Значит, не подходит.
При уравнение является квадратным
Аналогично способу 1 возможны варианты
1. 
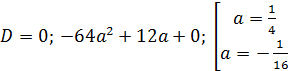
При получим
.
Значит, подходит
При получим
.
Значит, не подходит
2. 
Рассуждая аналогично способу 1, уравнение будет иметь ровно одно решение тогда и только тогда, когда из этих корней один удовлетворяет условию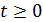 
, а другой нет.
Рассмотрим варианты
1. 
Снова рассуждая, как в способе 1 получим, что данное неравенство выполнено при
2. 
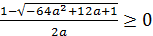
Снова рассуждая, как в способе 1 получим, что данное неравенство выполнено при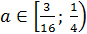
Концовка решения, снова как в способе 1 – получаем, что уравнение имеет единственное решение при
Ответ:
Способ 2 можно упростить, используя графические соображения, рассмотренные далее
3 способ (замена переменных + графические соображения)
Начинаем также как в способе 2
При получим . Значит, не подходит.
При уравнение является квадратным
Введём функцию 
Рассмотрим варианты
1. 
Тогда графиком функции является парабола, ветви которой направлены вверх, 
Уравнение будет иметь ровно одно положительное решение, если функция принимает в вершине нулевое значение (парабола 1 на рисунке) или если координата пересечения с осью ординат отрицательна (парабола 3 на рисунке)
Для параболы 1 получим
С учётом условия получим
Для парабол 2 и 3 получим
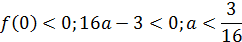
С учётом условия получим
2. 
Тогда графиком функции является парабола, ветви которой направлены вверх,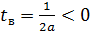 
Уравнение будет иметь ровно одно положительное решение, если координата пересечения с осью ординат равна 0 (парабола 1 на рисунке) или положительна (парабола 2 на рисунке)
Для парабол 1 и 2 получим
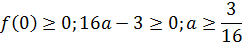
С учётом условия получим, что в данном варианте таких значений параметра нет.
Ответ:
4 способ (графические соображения + применение производной)
Рассмотрим функции 
и 
График функции 
– одна ветвь параболы с вершиной в начале координат, ветви идут вправо. График функции 
– прямая, принимающая различные положения в зависимости от значения параметра.
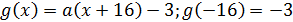
Таким образом – это пучок прямых, проходящих через точку 
Уравнение будет иметь единственное решение, если прямая касается параболы (прямая 1 на рисунке) или если прямая пересекает ординат ниже нуля, но имеет положительный наклон (расположена между прямыми 2 и 2 на рисунке)
Подумайте, почему именно такие положения прямых устраивают
Для случая касания (прямая 1) должно выполняться условие 
Отсюда 
Кроме того, в точке касания значения функций равны, то есть 
Получим 
, учитывая, что , получим
Прямая расположена горизонтально, если (прямая 3 на рисунке)
Прямая проходит через начало координат, если 
(прямая 2 на рисунке)
Отсюда необходимо, чтобы 
Значит, искомые значения параметра
Ответ:
Замечание: можно рассматривать различные функции, перенося в правую или левую части различные слагаемые