Урок №32-33
18.04.20
Тема «Практическое занятие № 5 «Звезды и галактики ». »
Цели урока: Освоить методику определения основных характеристик звезды по ее спектральному классу и абсолютной величине.
Содержание:
- Используя значения видимой и абсолютной звездных величин для своего варианта, определить расстояние до звезды в парсеках. Выразить это расстояние в световых годах и астрономических единицах. Найти параллакс звезды.
- Известны период обращения двойной звезды, большая полуось видимой орбиты и параллакс. Определить сумму масс и массы звезд в отдельности.
- Определить расстояние до галактики и ее диаметр. Исходными данными являются: скорость удаления галактики и видимый диаметр.
Общие сведения из теории
Со времен древнегреческого астронома Гиппарха (II в. до н.э.) используется понятие «звездная величина». Считая, что расстояния до звезд одинаковы, предполагали, что, чем звезда ярче, тем она больше. Наиболее яркие звезды отнесли к звездам первой величины (сокращенное обозначение 1m, от лат. magnitude — величина), а едва различимые невооруженным глазом — к шестой. В настоящее время известно, что видимая звездная величина характеризует не размеры звезды, а ее блеск, т.е. освещенность, которую создает звезда на Земле. Освещенность — световой поток, падающий на площадку в 1 см² поверхности.
Шкала звездных величин сохранилась и уточнена. Блеск звезды 1m больше блеска звезды 6m ровно в 100 раз. Следовательно, разность в 5 звездных величин соответствует различию в блеске ровно в 100 раз.
Отношение блеска двух звезд, видимые звездные величины которых известны, можно вычислить по формуле:
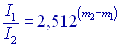
| (1) |
Светила, блеск которых превосходит блеск звезд 1m, имеют нулевые и отрицательные звездные величины (0m, -1m и т. д.). К ним относятся Солнце, Луна, несколько наиболее ярких звезд и планет. Видимая звездная величина Солнца -26,78. Шкала звездных величин продолжается и в сторону звезд, не видимых невооруженным глазом. Есть звезды 7m, 8m и т. д. Для более точной оценки блеска звезд используются дробные звездные величины 2,3m 7,1m 6,2m 14,5m и т. д.
Так как звезды находятся от нас на различных расстояниях, то их видимые звездные величины ничего не говорят о светимостях (мощности излучения) звезд. Поэтому в астрономии, кроме понятия «видимая звездная величина», используется понятие «абсолютная звездная величина».
Звездные величины, которые имели бы звезды, если бы они находились на одинаковом расстоянии (D0= 10 пк), называются абсолютными звездными величинами М.
Вся энергия, проходящая в единицу времени через замкнутую поверхность, окружающую данный источник — светимость L. Отношение светимостей двух звезд представим в виде формулы:
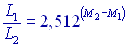
| (2) |
Cветимость звезды пропорциональна площади поверхности фотосферы (4πR2) и четвертой степени эффективной температуры (Т4)
| L = 4πR2σT4 | (4) |
Если в качестве одной из звезд выбрать Солнце, то
| или | 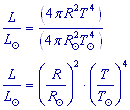
| (5) |
где буквы без индексов относятся к любой звезде, а со значком -к Солнцу.
Если известна светимость L и эффективная температура звезды, то, используя формулу (6.6), можно вычислить радиус звезды, ее объем и площадь фотосферы.
Для определения расстояний до звезд используется метод параллакса. Только в качестве базиса используется не радиус Земли, а средний радиус земной орбиты.
Угол π, под которым со звезды был бы виден средний радиус земной орбиты а, расположенный перпендикулярно направлению на звезду, называется годичным параллаксом звезды (рис. 1).
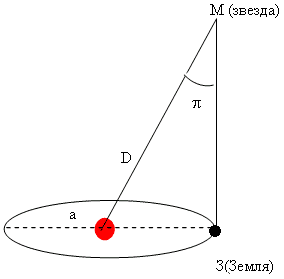
Рис.1. Годичный параллакс
В тех случаях, когда удается определить значение π, расстояние до звезды D вычисляется по формуле
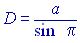
| (6) |
Параллакс всегда очень мал (меньше 1″). Поэтому формулу можно записать в виде:
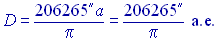
| (7) |
В звездной астрономии расстояния до далеких объектов измеряют в парсеках и световых годах, так как не только километр, но даже астрономическая единица (а.е.) слишком мала для измерения расстояний до звезд.
Парсек (пк) — расстояние, параллакс для которого равен 1″.
Световой год (св. г.) — расстояние, которое свет проходит за один год, распространяясь со скоростью 300 000 км/с.
1 пк = 206 265 а.е.=3,26 св.г.= 30,86 · 1013км.
1 св.г. = 9.46 · 1012км=63 240 а.е.=0.3 пк.
103 пк = 1 кпк (килопарсек);
106 пк = 1 Мпк (мегапарсек).
Очевидно, что расстояние до звезды в парсеках легко вычислить по формуле:
| D = 1/π | (8) |
Если известны видимая звездная величина и расстояние до звезды, абсолютную звездную величину можно вычислить по формуле
| M = m + 5 − 5 lg D | (9) |
где D — расстояние до звезды в парсеках.
Если известны видимая звездная величина и значение годичного параллакса звезды, формула (6.10) примет вид:
| M = m + 5 − 5 lg π | (10) |
Одной из важнейших характеристик звезды является ее масса. Массу звезды в массах Солнца можно вычислить по формуле
| μ / M = 3,89 · 10−0,1194 · M | (11) |
где μ — масса звезды,
М — абсолютная звездная величина звезды.
Определение средней плотности звезды, при известной ее массе и размерах, возможно по формуле
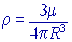
| (12) |
Третий закон Кеплера, уточненный Ньютоном, позволяет определить массу визуально — двойной звезды, если известен ее параллакс. Если А — большая полуось орбиты спутника, выраженная в а.е., Т — период обращения спутника около главной звезды, аз — большая полуось земной орбиты, Тз — период обращения Земли вокруг Солнца, m1 и m2 — массы звезд, М и mз — массы Солнца и Земли, то третий уточненный закон Кеплера можно выразить формулой:
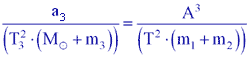
| (13) |
Заменим А соотношением
| A = a / π | (14) |
где a — большая полуось орбиты, выраженная в секундах дуги,
π — годичный параллакс звезды.
Так как большая полуось земной орбиты равна 1 а.е. и положив Тз=1, mз=0, массы звезд, выраженные в массах Солнца, можно вычислить по формуле
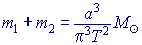
| (15) |
Классификация звезд.
Звезды чрезвычайно неоднородный класс астрономических объектов. Разнообразие звезд связано с двумя причинами: различием их масс и различием этапов эволюции, на которых они находятся в момент наблюдения.
Звезды можно классифицировать различными способами. Чаще используется деление звезд на спектральные классы и классы светимости.
Спектральные классы звезд определяются по особенностям звездных спектров и непосредственно связаны с температурой их поверхности. Используемая в настоящее время система насчитывает восемь спектральных классов и два ответвления:
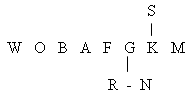
которые охватывают 90% всех звезд.
Данную классификацию можно легко запомнить, воспользовавшись выражением: "Вообразите, Один Бритый Англичанин Финики Жевал Как Морковь. Разве Не Смешно". Интервал между двумя спектральными классами разделяется на 10 подклассов. Спектральный класс тесно связан с цветом звезды. Зависимость спектральных классов и показателей цвета звезд от их температур представлено в таблице 1.
Таблица 1.
Зависимость спектральных классов и показателей цвета звезд от их температур
| Спектральный класс | Цвет | Температура, К |
| W | белый | 100 000 |
| O | 50 000 | |
| B0 | голубой | 25 000 |
| B5 | 15 000 | |
| A0 | 11 000 | |
| A5 | 8 700 | |
| F0 | желтый | 7 600 |
| F3 | 6 600 | |
| G0 | 6 000 | |
| G5 | 5 520 | |
| K0 | красный | 5 120 |
| K5 | 4 400 | |
| M0 | 3 600 | |
| M5 | 2 700 |
Классы светимости связаны с истинной интенсивностью излучения звезд. В пределах одного и того же спектрального класса (т.е. при одинаковых цвете и температуре поверхности) у звезд могут быть очень разные физические параметры.
Основные классы светимости:
I. Сверхгиганты.
II. Яркие гиганты.
III. Гиганты.
IV. Субгиганты.
V. Карлики главной последовательности.
VI. Субкарлики.
VII. Белые карлики.
При описании звезды класс светимости пишется справа от спектрального класса: так, Солнце — это звезда типа G2V.
Достаточно знать спектральный класс звезды и ее абсолютную звездную величину, чтобы определить все основные характеристики звезды: температуру, радиус, светимость, объем, площадь фотосферы, массу и плотность.
Галактика.
В начале ХХ века было доказано, что туманные пятна, видимые в телескоп в разных участках неба, представляют собой галактики, каждая из которых, подобно нашей, состоит из миллиардов звезд. Существует несколько методов определения расстояний до галактик.
Один из методов определения основан на определении видимых и абсолютных звездных величин цефеид, новых и сверхновых звезд, открываемых в других галактиках. По формуле (6.20) можно вычислить расстояние до тех галактик, в которых обнаружены цефеиды, новые и сверхновые звезды.
О расстояниях до удаленных галактик, в которых перечисленные объекты не видны, судят по их видимым угловым размерам или по видимой звездной величине. Для этого необходимо знать размеры или светимости галактик данного типа.
Наконец, еще один способ основан на определении величины красного смещения.
В ХХ веке человечество свыклось с еще более странным фактом: расстояния между звездными системами — галактиками, не связанными друг с другом силами тяготения, постоянно увеличивается. И дело здесь не в природе галактик: сама Вселенная непрерывно расширяется!
В 1929 г. американский астроном Эдвин Хаббл подтвердил расширение видимой части Вселенной. Он использовал при этом эффект Доплера. Линии в спектре движущегося источника смещаются на величину, пропорциональную скорости его приближения или удаления. Исследовав спектры нескольких галактик, астрономы заметили, что у большинства из них спектральные линии смещены в красную сторону. Смещение линий в сторону длинных волн в спектре, который получен от далекого космического источника (галактики, квазары), по сравнению с длинами волн тех же линий, измеренными от неподвижного источника, называется красным смещением.
Закон, по которому скорость удаления пропорциональна расстоянию, получил названия закона Хаббла. Если скорость невелика по сравнению со скоростью света (с = 300000 км/с), она выражается простой формулой
| ν = H · r | (16) |
где ν — лучевая скорость галактики, выраженная в км/с;
r — расстояние до нее, выраженное в Мпк;
Н — постоянная Хаббла.
По современным оценкам, значение Н заключено в пределах
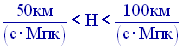
Пример решения задач
Задача 1. Во сколько раз звезда 3,4 звездной величины выглядит слабее, чем Сириус, имеющий видимую звездную величину — 1.6? Чему равны абсолютные величины этих звезд, если расстояние до обеих составляет 3 пк?
| Дано: | Решение: | |
| m1=−1,6 m2=3,4 D=3пк | I1/I2=2,512m2−m1, M=m + 5−5 lg D | I1/I2=2,5123,4+1,6= 100; M1=−1,6+5−5 lg 3 = 1; M2=3,4+5−5 lg 3 = 6. |
| Найти: I1/I2=? M1=? M2=? |
Ответ: В 100 раз Сириус ярче. M1 = 1, M2 = 6.
Задача 2. Какова светимость звезды ζ Скорпиона, если ее видимая звездная величина 3, а расстояние до нее 7500 св. лет?
| Дано: | Решение: | |
| М=4,8 m = 3 D=7500 св.лет | L=2,512M−M M = m + 5−5 lg D 1 пк = 3,26 св.лет | D пк = 2300 пк M = 3+5−5 lg 2300 = −8,8; L=2,5124,8−(−8,8;)≈3,3·105. |
| Найти: L=? |
Задача 3. У двойной звезды период обращения 100 лет. Большая полуось видимой орбиты a = 2″, а параллакс π = 0.05″. Определите сумму масс и массы звезд в отдельности, если звезды отстоят от центра масс на расстояниях, относящихся как 1:4.
| Дано: | Решение: | |
| T = 100 лет a = 2″ π = 0,05″ A2 / A1 = 1/4 | Отсюда 5m1=6,4 массы Солнца. m1≈1,3 массы Солнца, m2≈5,1 массы Солнца. | |
| Найти: (m1+m1)=? m1=? m1=? |
Ответ: Сумма масс двойной звезды равна 6,4 массы Солнца; m1≈1,3; m2≈5,1.
Домашнее задание: Изучить урок, примеры задач записать в тетрадь
Обратная связь
Выполненное задание присылайте:
В группу согласно расписанию
e-mail: r.r-ko@yandex.ru