Общая схема исследования функции и построения графиков

Найти ОДЗ и точки разрыва функции.Найти точки пересечения графика функции с осями координат.Провести исследование функции с помощью первой производной, то есть найти точки экстремума функции и интервалы возрастания и убывания.Исследовать функцию с помощью производной второго порядка, то есть найти точки перегиба графика функции и интервалы его выпуклости и вогнутости.Найти асимптоты графика функции: а) вертикальные, b) наклонные.На основании проведенного исследования построить график функции.

Заметим, что перед построением графика полезно установить, не является ли данная функция четной или нечетной.Вспомним, что функция называется четной, если при изменении знака аргумента значение функции не меняется: f(-x) = f(x) и функция называется нечетной, если f(-x) = -f(x).В этом случае достаточно исследовать функцию и построить её график при положительных значениях аргумента, принадлежащих ОДЗ. При отрицательных значениях аргумента график достраивается на том основании, что для четной функции он симметричен относительно оси Oy, а для нечетной относительно начала координат.

15)Первообра́зной данной функции f называют такую F,производная

которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием. Если F — первообразная f, и функция f определена на каком-либо интервале, тогда каждая последующая первообразная G отличается от F на константу: всегда существует число C, такое что G(x) = F(x) + C для всех x. Число C называют постоянной интегрирования.

Множество первообразных функции f(x) называется неопределённым интегралом от этой функции и обозначается символом .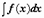
F(x) - некоторая первообразная функции f(x), то , где C - произвольная постоянная. Функцию f(x) принято называть подынтегральной функцией, произведение f(x) dx - подынтегральным выражением.

16)Задача нахождения неопределенного интеграла заключается в нахождении такой функции, производная которой равняется подынтегральному выражению. Данная функция определяется с точностью до постоянной, т.к. производная от постоянной равняется нулю. формулу интегрирования по частям

или

С помощью формулы интегрирования по частям вычисляется достаточно большой класс неопределенных интегралов. Во многих случаях, применяя данную формулу, это есть единственный способ вычислить интеграл.

Для применения данной формулы, необходимо подынтегральную функцию разбить на произведение двух функций, одна из которых является производной, далее применить формулу интегрирования по частям. Замена переменной: Положив в , что , т.е. переменная является функцией от 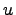, тогда

получим выражения для и . Теперь подставим полученные выражения в интеграл, следовательно:

где 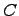--произвольная постоянная и функция -- обратная функция к . Такое преобразование интеграла называется интегрированием подстановкой (замена переменных).

Замечание. Последнее действие в предыдущем равенстве является обязательным, т.к. интеграл зависит от переменной , следовательно, ответ должен быть функцией от . Это операция называется - обратная замена переменных.

Общая замена переменных выглядит следующим образом:

тогда

и, используя эти равенства, добиваемся, чтобы в исходном интеграле, зависящим от , не было вхождения , т.е.

Здесь следуя предыдущему замечанию необходимо сделать обратную замену переменных. Отметим, что если изначально, например, интегрировали по , то ответ не должен содержать других переменных кроме .

17)Определенный интеграл от функции: Предел от суммы при , если он существует и конечен, называется определенным интегралом от функции в пределах от до и обозначается:

 

Свойства определённого интеграла: 1) Линейность. Если функции y = f(x), y = g(x) интегрируемы по отрезку [a,b], то по этому отрезку интегрируема их линейная комбинация A f(x) + B g(x) (A, B = const), и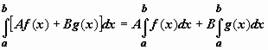

2) Аддитивность. Если y = f(x) интегрируема по отрезку [a,b] и точка c принадлежит этому отрезку, то 3) Теорема об интегрировании неравенств. Если в любой точке выполняется неравенство , и функции f(x), g(x)интегрируемы по отрезку [a,b], то .

 

18)Формула Ньютона-Лейбница. Если f(x) непрерывна на отрезке [a, b], и F(x) - некоторая первообразная функции , то 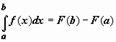. Формула интегрирования по частям для определённого интеграла. Если u(x), v(x) - непрерывно дифференцируемые функции, то . Замена переменной в определённом интеграле. Теорема. Пусть функция 1)определена, непрерывно дифференцируема и монотонна на отрезке ,2) ,3)функция непрерывна на отрезке [a, b].Тогда .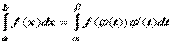

Таблица дифференциалов

19)Производная обратной функции: Пусть - дифференцируемая функция от аргумента x в некотором интервале . Если в уравнении y считать аргументом, а x - функцией, то возникает новая функция , где - функция обратная данной.Пример: Дифференцирование функций, заданных параметрически: Пусть задана зависимость двух переменных и 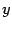от параметра , изменяющегося в пределах от до :

Пусть функция имеет обратную: . Тогда мы можем, взяв композицию функций и , получить зависимость 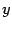от : . Зависимость величины 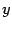от величины , заданная через зависимость каждой из них от параметра в виде , называется функцией , заданной параметрически.

Производную функции , заданной параметрически, можно выразить через производные функций и : поскольку и, по формуле производной обратной функции, , то

где -- значение параметра, при котором получается интересующее нас при вычислении производной значение .

Заметим, что применение формулы приводит нас к зависимости между и , снова выраженной в виде параметрической зависимости: , ; второе из этих соотношений -- то же, что участвовало в параметрическом задании функции . Несмотря на то, что производная не выражена через в явном виде, это не мешает решать нам задачи, связанные с нахождением производной, найдя соответствующее значение параметра .

20)Определение несобственного интеграла по бесконечному промежутку. Пусть функция f(x) определена на полуоси и интегрируема по любому отрезку [a,b], принадлежащему этой полуоси. Предел интеграла при 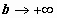называется несобственным интегралом функции f(x) от a до и обозначается .
Итак, по определению, . Если этот предел существует и конечен, интеграл называется сходящимся; если предел не существует или бесконечен, интеграл называется расходящимся. Формула Ньютона-Лейбница для несобственного интеграла. В приведённых примерах мы сначала вычисляли с помощью первообразной функции определённый интеграл по конечному промежутку, а затем выполняли предельный переход. Объединим два этих действия в одной формуле. Символом 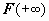будем обозначать ; символом - соответственно, ; тогда можно записать , , 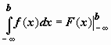, подразумевая в каждом из этих случаев существование и конечность соответствующих пределов. Теперь решения примеров выглядят более просто: - интеграл сходится; 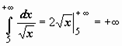- интеграл расходится.

Для несобственных интегралов применимы формулы интегрирования по частям и замены переменной: ; при замене переменной несобственный интеграл может преобразовываться в собственный. Так, например, вычислим интеграл: 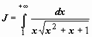. Пусть 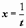, ; если , то ; если то ; 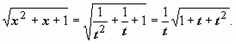Поэтому (это уже собственный интеграл) = .

21)Вычисление площади в декартовых координатах

Если плоская фигура ограничена прямыми x=a, x=b, a<b, и кривыми , то ее площадь вычисляется по формуле

(рис. 1).

Аналогично можно рассматривать фигуру относительно оси ОУ.

В некоторых случаях границы х=а и х=b могут вырождаться в точку пересечения кривых .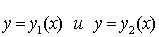

В сложных случаях область следует разбить на фигуры, границы которых удовлетворяют указанным соотношениям.

При решении задач удобно придерживаться следующего порядка:

- построить в декартовых координатах фигуру, площадь которой требуется найти;

- найти точки пересечения кривых, образующих границу области для определения пределов интегрирования;

- записать формулу для вычисления и найти площадь.

Вычисление площади в полярных координатах

Пусть фигура представляет собой сектор, заданный в полярной системе координат кривой , где - неотрицательная непрерывная кривая на отрезке . Разобьем угол на nчастей лучами < <…< и обозначим

Площадь криволинейного сектора равна сумме n площадей , заданных разбиением , i = 1, 2, …, n, .Выберем один из элементов разбиения , соответствующий сектору , и зафиксируем на этом промежутке произвольное значение 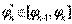. Значение функции в точке обозначим и заменим площадь криволинейного сектора круговым сектором радиуса , площадь которого . Выполним такую же операцию на каждом участке разбиения и просуммируем полученные значения.Сумма площадей круговых секторов представляет собой интегральную сумму, предел которой, существующий в силу непрерывности функции , равен определенному интегралу, выражающему площадь фигуры в полярных координатах При вычислении площади фигуры в полярных координатах рекомендуется придерживаться такого же порядка исследования, что и в декартовых координатах: построение чертежа, вычисление точек пересечения кривых, образующих границу фигуры; запись формулы.

22)Определение несобственного интеграла по бесконечному промежутку. Пусть функция f(x) определена на полуоси и интегрируема по любому отрезку [a,b], принадлежащему этой полуоси. Предел интеграла при 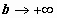называется несобственным интегралом функции f(x) от a до и обозначается . Итак, по определению, . Если этот предел существует и конечен, интеграл называется сходящимся; если предел не существует или бесконечен, интеграл называется расходящимся. Признаки сравнения для неотрицательных функций. В этом разделе мы будем предполагать, что все подынтегральные функции неотрицательны на всей области определения. До сих пор мы определяли сходимость интеграла, вычисляя его: если существует конечный предел первообразной при соответствующем стремлении (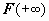 или ), то интеграл сходится, в противном случае - расходится. При решении практических задач, однако, важно в первую очередь установить сам факт сходимости, и только затем вычислять интеграл (к тому же первообразная часто не выражается через элементарные функции). Сформулируем и докажем ряд теорем, которые позволяют устанавливать сходимость и расходимость несобственных интегралов от неотрицательных функций, не вычисляя их.

 

 

 

25)Формула Тейлора показывает поведение функции в окрестности некоторой точки. Формула Тейлора функции часто используется при доказательстве теорем в дифференциальном исчислении.

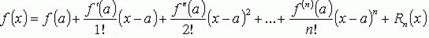
, где R_n(x) - остаточный член формулы Тейлора.