Практическое занятие № 5.
Основные понятия теории вероятностей.
Действия с вероятностями.
Ø Изучите материалы лекций 4 и 5.
Ø Ответьте на контрольные вопросы к занятию.
Контрольные вопросы
1. Что такое «испытание», «событие»? Приведите примеры испытаний и событий.
2. Какие события называются совместными и несовместными?
3. В каком случае два события называются противоположными? Приведите примеры несовместных и противоположных событий.
4. Что такое «достоверное событие», «невозможное событие», «случайное событие», «полная группа событий», «элементарные события/исходы»?
5. Дайте классическое определение вероятности.
6. Что такое абсолютная и относительная частота события А? Сформулируйте статистическое определение вероятности.
7. Сформулируйте геометрическое определение вероятности. Приведите примеры.
8. Что такое сумма и произведение событий? Приведите примеры.
9. Какие события называются независимыми? Зависимыми? Приведите примеры.
10. Сформулируйте теоремы о вероятности суммы несовместных событий.
11. Сформулируйте теоремы о вероятности суммы совместных событий.
12. Сформулируйте теоремы о вероятности произведения независимых событий.
13. Дайте определение условной вероятности. Сформулируйте теоремы о вероятности произведения зависимых событий.
Ø При выполнении заданий практического занятия № 5 используйте ваши знания по темам: «Комбинаторика. Правила и формулы комбинаторики»,
«Основные понятия теории вероятностей», «Действия с вероятностями»
Ø Используйте материалы лекций №№ 3, 4, 5,
Ø а также другие источники (учебники, интернет)
Непосредственное нахождение вероятности событий —
вычисление вероятности событий по определению.
Ø При решении задач 1.1-1.8 установите, о каком испытании (опыте) идёт речь в задачной ситуации;
Ø какое определение вероятности искомого события применяется для решения задачи;
Ø как можно использовать комбинаторные соединения при подсчёте числа всех возможных исходов опыта и числа исходов, благоприятных для данного события.
ü Во многих задачах в первую очередь используется классическая формула вычисления вероятности события.
Если производится некоторый опыт, имеющий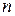 
равновозможных исходов, из которых 
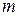исходов благоприятствуют наступлению события А, то вероятность события А, обозначаемая 
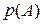или просто 
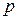, равна отношению числа благоприятствующих исходов к общему числу исходов опыта:
.
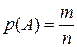1.1. В соревнованиях по толканию ядра участвуют 4 спортсмена из Эстонии, 6 спортсменов из Латвии, 3 спортсмена из Литвы и 7 — из Польши. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Литвы.
Решение. В соревнованиях участвуют 4 + 6 + 3 + 7 = 20 спортсменов. Следовательно, общее число мест для выступлений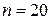 
. Три из них предназначены спортсменам из Литвы, т. е. т = 3. Т.к. порядок выступлений определяется жребием, то вероятность литовским спортсменам занять любое место из них, в том числе и последнее, одинакова и равна 
.
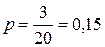1.2. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 2, но не дойдя до отметки 5 часов.
Решение. Благоприятствующими для наступления нужного события будут 3 деления из 12. Тогда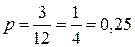 
.
1.3. Покупая карточку лотереи «Спортлото», игрок должен зачеркнуть 6 из 49 возможных чисел от 1 до 49. Если при розыгрыше тиража лотереи он угадает все 6 чисел, то имеет шанс выиграть значительную сумму денег. Чему равна вероятность угадать все 6 номеров?
Решение. Так как число исходов данного опыта конечно, и все они равновозможны, используем классическую формулу вычисления вероятности: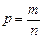 
.
Общее число исходов опыта n равно числу способов выбрать 6 чисел из 49, при этом порядок выбора значения не имеет, значит, считаем число сочетаний из 49 по 6:
.
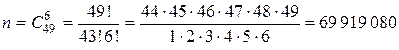К сожалению, благоприятный вариант только один.
Тогда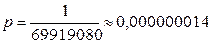 
.
1.4. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орел не выпадет ни разу.
Решение. При одном бросании монеты практически возможны два исхода: выпадение герба, орла (О) или цифры, решки (Р). Т.к. монета симметрична, то вероятности этих вариантов одинаковы. При двух бросаниях монеты возможны 4 (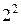
) исхода: ОО, ОР, РО, РР. При трёх бросаниях монеты возможны 8 (
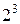) исходов: ООО, ООР, ОРО, РОО, ОРР, РОР, РРО, РРР.
??? Какие комбинаторные соединения здесь применяются?
??? Применима ли здесь формула размещения с повторениями?
В общем случае при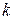 
бросаниях монеты будет 
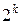исходов. В нашем случае 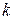= 4, следовательно, 
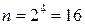. Благоприятствующим будет только один вариант.
Тогда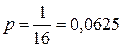 
.
1.5. В случайном эксперименте симметричную монету бросают пять раз. Найдите вероятность того, что орел выпадет ровно 4 раза.
Решение. Учитывая решение задачи 1.4, найдём, что общее число исходов опыта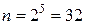 
. Рассмотрим благоприятствующие исходы: ООООР, ОООРО, ООРОО, ОРООО, РОООО, их пять. Тогда 
.
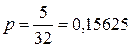1.6. В группе туристов 8 человек. С помощью жребия они выбирают двух человек, которые должны идти в село за продуктами. Турист Б. хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что Б. пойдёт в магазин?
Решение. Опыт состоит в том, что выбирают двоих человек из восьми (важен ли порядок выбора?), общее число исходов такого опыта равно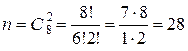 
.
Благоприятствующими будут те способы, когда выбранная пара состоит из туриста Б. (его можно выбрать 1 способом) и кого-то из оставшихся 7 туристов. Согласно правилу произведения число благоприятствующих способов будет равно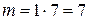 
. Тогда искомая вероятность равна 
.
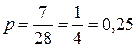1.7. В классе 33 учащихся, среди них два друга — Андрей и Михаил. Класс случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Андрей и Михаил окажутся в одной группе.
Решение. Общее количество способов создать группу в одиннадцать человек из тридцати трёх равно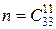 
. (Почему?)
Благоприятствующими будут те способы, когда два друга будут вместе в одной из трёх групп, а оставшиеся девять человек будут произвольным образом выбраны из тридцати одного: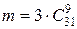 
. (Что означает множитель 3?)
Тогда
.
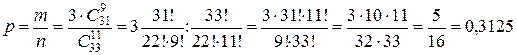К задаче 1.8.
??? Можно ли решить следующую задачу, используя классическое определение вероятности события?
1.8. Две грузовых машины могут подойти на погрузку в промежуток времени от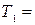 
17 часов до 
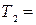18.30. Погрузка первой машины длится 
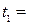10 минут, второй – 
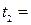5 минут. Найти вероятность того, что одной из машин придётся ждать окончания погрузки другой.
Решение.
??? Что можно сказать об общем числе исходов испытания? Является ли оно конечным?
??? Можно ли установить число благоприятствующих исходов? Почему?
??? Можно ли решить данную задачу, используя классическое определение вероятности события?
Ø Используем геометрическое определение вероятности. Составим геометрическую модель задачи, введя необходимые обозначения.
Ø При построении чертежа выберите удобный масштаб (1 кл. - 10 мин.)
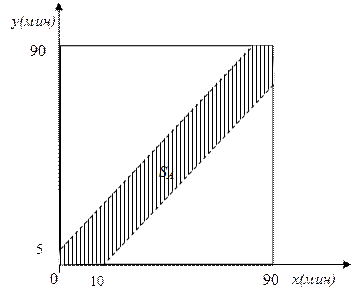Пусть первая машина подошла на погрузку через x минут после 17 часов, а вторая – через y минут. Тогда время прибытия машин можно изобразить точкой на координатной плоскости. Так как обе координаты могут принимать значения от 0 до 
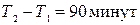, то все возможные исходы данного опыта будут представлены точками квадрата со стороной, равной 90 минут.
Исходы, благоприятствующие искомому событию А – одной из машин придётся ожидать окончания погрузки другой, изобразятся точками той части квадрата, которые являются решением системы неравенств: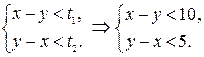 
Чтобы изобразить указанную область, нарисуем прямые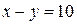 
и 
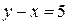. Для удобства уравнения этих прямых можно преобразовать к виду: 
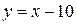и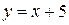 
. Первая прямая проходит через точки (10; 0) и (90; 80). Вторая прямая проходит через точки (0; 5) и (85; 90). Нарисованные прямые делят квадрат на три части. Подставив координаты точки из средней части квадрата, например, точки (45; 45), убеждаемся, что оба неравенства выполняются в средней части квадрата, заштрихованной на рисунке.
Искомая вероятность будет равна отношению заштрихованной площади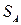 
к площади квадрата. Величину 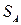можно найти, вычтя из площади квадрата площадь двух прямоугольных треугольников.
.
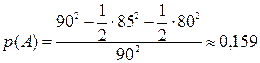Ответ: 0,159.