ü Часто в задачах нужно найти вероятность события, составленного из других событий при помощи действий.
??? Какие действия с событиями вы знаете?
??? В чём они состоят?
??? Как вычислить вероятности составных событий?
Ø В следующих утверждениях 1*-10* вставьте недостающие термины и/или формулы:
1*. Если событие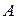 
состоит в осуществлении хотя бы одного из событий
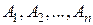, то говорят,
что событие 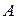равно ................................... событий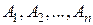
и записывают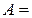 
.....................................
2*. Несколько событий называются несовместными в данном опыте,
если ......................................(?) могут произойти вместе.
Несколько событий называются совместными в данном опыте,
если ......................................(?) могут произойти вместе.
3*. Вероятность события А, являющегося суммой несовместных событий
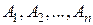, равна .............................. вероятностей отдельных событий:
...............................
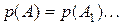4*. Вероятность события А, являющегося суммой совместных событий
А1 и А2, равна..............................
5*. Если событие 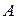состоит в ................................ осуществлении событий
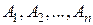, то говорят, что
оно равно произведению событий 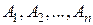и записывают
.
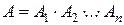6*. Вероятность события А, являющегося
произведением независимых событий ,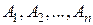
равна .............................. вероятностей отдельных событий:
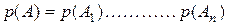
7*. Независимыми называются события,
вероятность которых ...................... от того,
произошло другое событие или нет.
Зависимыми называются события,
вероятность которых .................. от того,
произошло другое событие или нет.
8*. Вероятность события А, являющегося
произведением зависимых событий А1 и А2,
вычисляется по формуле: ...........................................
9*. Событие, состоящее в ненаступлении события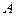 
,
называется .............................. ему и обозначается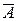 
.
|
|
10*. Сумма вероятностей противоположных событий
равна .........................: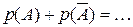 
.
Ø В следующих задачах при анализе событий опишите их взаимосвязь: являются ли группы событий совместными/несовместными, зависимыми/независимыми, как выражается искомое событие через другие составляющие его события.
Ø Выразите взаимосвязь событий формулой, при необходимости введите нужные обозначения.
Ø Укажите формулы для вычисления вероятности каждого составного события, зная вероятности элементарных событий.
2.1. На экзамене по математике студенту достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Числовые ряды», равна 0,1. Вероятность того, что это вопрос на тему «Классическая вероятность», равна 0,35. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене студенту достанется вопрос по одной из этих двух тем.
Решение. Событие 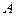(студенту достанется вопрос по одной из двух указанных тем) состоит в осуществлении одного из двух событий:
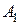- студенту достанется вопрос по теме «Числовые ряды»,
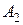- студенту достанется вопрос по теме «Классическая вероятность».
Следовательно, событие А является их суммой: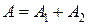 
.
Тогда, т.к. события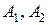 
несовместны, то
.
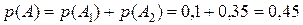2.2. Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,7. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Решение. Событие - биатлонист первые два раза попал в мишень, последние два раза промахнулся, будет совместным осуществлением, т.е. произведением четырёх событий: 
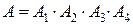, где
|
|
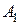- при первом выстреле попал,
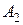- при втором выстреле попал,
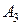- при третьем выстреле промахнулся,
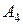- при четвёртом выстреле промахнулся.
??? Какими являются эти события между собой – зависимыми или независимыми?
??? Как вычислить вероятность события А?
Поскольку данные элементарные события являются независимыми,
следовательно,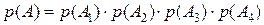 
.
Поскольку события «попал» и «промахнулся» являются противоположными, то вероятность промаха равна 1 – 0,7 = 0,3.
С учётом этого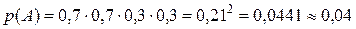 
.
2.3. По отзывам покупателей Пётр Петрович оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,87. Вероятность того, что этот товар доставят из магазина Б, равна 0,92. Пётр Петрович заказал товар сразу в обоих магазинах.
Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.
Решение. Событие 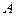- товар не доставит ни один магазин, произойдёт, если совместно произойдут два события А1 и А2:
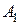- товар не доставит первый магазин,
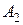- товар не доставит второй магазин.
Таким образом,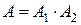 
.
??? Какими являются события А1 и А2: зависимыми или независимыми?
??? Как найти вероятность произведения независимых событий?
Ø Запишите необходимые формулы.
Ø Выразите вероятности каждого из событий, исходя из условия задачи.
Ø Чему равна искомая вероятность?
??? Так ли у вас получилось?
.
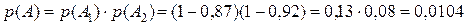ü Довольно часто при решении задач нужно использовать не одно действие с событиями, а сразу оба. Причём бывают самые разные комбинации этих действий.
|
|
2.4. Чтобы поступить в институт на специальность «Международные отношения», абитуриент должен набрать на ЕГЭ не менее 79 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 79 баллов по каждому из трёх предметов — математика, русский язык и обществознание.
Вероятность того, что абитуриент И. получит не менее 79 баллов по математике, равна 0,8, по русскому языку — 0,7, по иностранному языку — 0,9 и по обществознанию — 0,5.
Найдите вероятность того, что И. сможет поступить на одну из двух упомянутых специальностей.
Решение. Событие 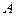- абитуриент поступит на одну из упомянутых специальностей, произойдёт при наступлении одного из двух событий:
М – абитуриент поступит на «Международные отношения»,
К – абитуриент поступит на «Коммерцию».
Следовательно, А = М + К.
Событие М будет совместным осуществлением, т.е. произведением трёх событий:
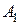- абитуриент получил по математике не менее 79 баллов,
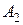- абитуриент получил по русскому языку не менее 79 баллов,
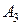- абитуриент получил по иностранному языку не менее 79 баллов.
Событие К будет совместным осуществлением, т.е. произведением трёх событий:
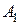- абитуриент получил по математике не менее 79 баллов,
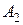- абитуриент получил по русскому языку не менее 79 баллов,
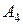- абитуриент получил по обществознанию не менее 79 баллов.
Ø Запишите формулу для события А.
.............................................................................................................................
Ø Как вычислить его вероятность?
..............................................................................................................................
Ø Проверьте себя:
Следовательно, событие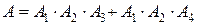 
.
Вероятность события А находится по формуле:
=
= 
.
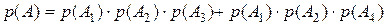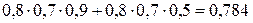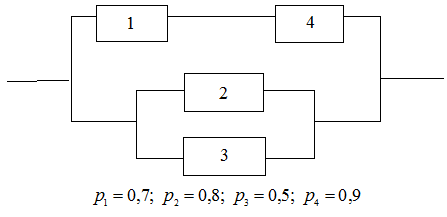2.5.
Определите надёжность схемы, представленной на рисунке, где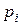 
- вероятность
безотказной работы
i-того элемента.
(Под надёжностью схемы понимается вероятность безотказной работы схемы.)
Решение. Соединение элементов, представленное на схеме, является комбинированным, так как содержит и последовательное, и параллельное соединение. Напомним, что
при последовательном соединении система работает,
если работают все элементы, соединённые последовательно;
и не работает, когда не работает хотя бы один элемент.
При параллельном соединении система работает,
если работает хотя бы один элемент системы;
и не работает, когда не работает ни один элемент.
Выделим участок схемы, содержащий последовательное соединение элементов (1) и (4) в отдельный элемент (5). Участок схемы, содержащий параллельное соединение элементов (2) и (3), выделим в элемент (6).
Обозначим В – событие, состоящее в том, что элемент (5) работает,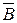 
- противоположное событие, состоящее в том, что элемент (5) не работает.
Событие С – это безотказная работа элемента (6),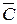 
- событие состоящее в том, что элемент (6) не работает.
Событие, состоящее в том, что работает вся схема, обозначим А. Так как элементы (5) и (6) соединены параллельно, то для наступления события А необходимо, чтобы работал хотя бы один из элементов (5) и (6):
1 сл. – работают оба,
2 сл. – работает (5) и не работает (6),
3 сл. – не работает (5) и работает (6).
Тогда событие А: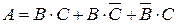 
.
Все три варианта наступления события А несовместны,
а в каждом случае работы блоков 5 и 6 события являются независимыми.
Соответственно, его вероятность
.
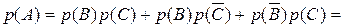
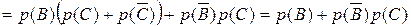Учитывая, что элемент 5 содержит последовательное соединение 1 и 4 элементов, вероятность его работы равна произведению вероятностей безотказной работы каждого из этих элементов: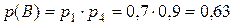 
Тогда,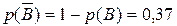 
.
Для нахождения вероятности события С рассмотрим противоположное ему событие 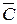- событие, состоящее в том, что элемент (6) не работает. Элемент 6 состоит из параллельно соединённых 2 и 3 элементов, тогда он не работает, когда не работают оба элемента 2 и 3:
; 
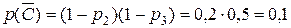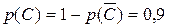
Таким образом, для вероятности события А получим:
.
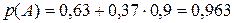Ответ: вероятность безотказной работы схемы равна 0,963.
??? Какова вероятность безотказной работы блока 5?... блока 6?
??? Как по-другому можно вычислить вероятность события А?
2.6.
??? Какими являются события А, В и С: зависимыми или независимыми?
Решите задачу 2-м способом.
??? Сколькими способами можно выбрать 3человек из всех 10?
??? Сколькими способами можно сделать выбор 3-х мужчин?
Ø Запишите с помощью комбинаторных соотношений эти результаты.
......................................................................................................................................
??? Как вычислить вероятность события А*В*С?
.....................................................................................................................................
Ø Сравните результаты решения 2-мя способами. Сделайте вывод.
Ø Какой из способов для вас является более предпочтительным?
2.7. Из урны, в которой находится 10 белых и 5 черных шаров,
вынимаем 2 шара. Найт и вероятность того, что:
А) оба шара белые,
Б) оба шара чёрные,
В) шары разных цветов.
Решение: а) оба шара белые (два способа решения).
1 способ. Пусть шары вынимаются последовательно, один за другим.
Рассмотрим два события: А –«первый шар белый», В – «второй шар белый».
Тогда, событие « оба шара белые» - это А*В.
??? Верно ли что Р(АВ)= Р(А) *Р(В)?
??? Какими являются события А и В: зависимыми или независимыми?