S сфероидической тр-ции. Размеры рамок тр-ций топографических карт
Тр-ция топокарты люб. м-ба явл. отображением на пл-ти в соотв-й проекции сфероидической тр-ции, ограниченной мерид. и паралл. с соотв-й разграфке м-бных рядов разностью долгот и широт. Например, для м-ба 1: 1 000 000 у нас в стране эти разности приняты соотв-но в 60 и 40. В других странах принята иная разграфка. Везде стремятся к тому, чтобы линейные размеры тр-ций карт люб. м-ба были бы примерно одинаковыми.
Пусть мы имеем такую сфероидическую трапецию. Тогда S пов-ти элл-да, ограниченная парами мерид. и паралл.определяется двойным интегралом
Подынтегральное выражение преобразуем. Для этого перейдем к первому эксцентриситету по известной ф-ле e/2 = e2 / (1 – e2), в рез-те получим
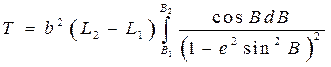(4. 33)
Используя новую переменную по ф-ле esinB = sinQ, будем иметь
cosB dB = ( cosQ dQ) / e.
В рез-те имеем после очевидных преобразований и интегрирования
(4. 34)
Возвращаясь от переменной Q к широте В, получим
(4. 35)
Вычисление площади по полученной ф-ле производится при условии, что разность долгот берется в радианной мере. При этом точность вычислений зависит только от их разрядности, так как ф-ла (4. 35) строгая.
Прежде чем приступить к ф-лам для вычислений размеров рамок топографических карт, полезно заметить следующее. Во – первых, эти размеры нужны для вычерчивания рамок соответствующего м-ба карт, когда предельная графическая точность равна 0. 1 мм в м-бе карты. Во – вторых, линейные размеры тр-ций карты люб. м-ба примерно одинаковы и не превосходят величины 50 х 50 см. В – третьих, численные значения размеров рамок нужны для их нанесения на планшет и вычерчивания с графической точностью (до 0. 1 мм). Т.о. мы видим, что в любом случае при вычислениях необходимо учитывать не более 4 значащих цифр.
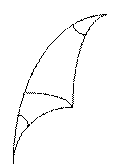
На рисунке 4.4 показана тр-ция топокарты, у к-рой основаниями явл. изображения на пл-ти параллелей, а боко
Рис. 4. 4 | выми сторонами – изображения меридианов элл-да. Для вычисления их длин воспользуемся ранее полученными ф-лами для малой дуги меридиана и параллели, при этом будем иметь в виду, что карта м-ба 1: m, линейные параметры элл-да даны в метрах. С учетом этого имеем |
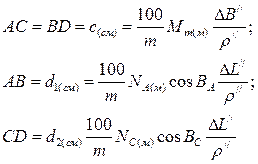(4. 36)
С-ма дифференциальных ур-ний геодез. линии
На рисунке 4. 5 имеем полярный сфероидический тр-к PTK,
Рис. 4. 5 | у к-ого Р – полюс, T и K – бесконечно близкие друг другу точки, соединенные элементарной дугой геод. линии dS, проходящей ч/з т. T в азимуте А. Ч/з т. К ( широта к-рой равна В) проведем параллель, к-рая пересечет мерид. т. Т в нек-рой т. С. Рассмотрим элементарный прямоуг. тр-к ТСК у к-ого все стороны будут бескон. малы потому, что гипотенуза dS по условию бескон. мала. Этот тр-к решаем как плоский прямоуг., при этом будем иметь в виду, что элем. дуга мерид. ТС равна M dB, а паралл. СК - rdL, где d L – разность долготт. К и Т. РЗ |
В рез-те можем записать.
M dB = dS cos A; r dL = dS sin A, (4. 37)
откуда получаем дифференциальные зависимости
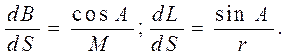(4. 38)
Обратимся теперь к треуг. РTК. Не смотря на то, что одна из его сторон T К бесконечно мала, стороны РT и РК могут достигать значительных величин, зависящих от значения широты точки Т. В этом случае мы можем рассматривать его как сферический и решать по ф-лам сферической тригонометрии. Угол при вершине Р равен dL, при вершине T – азимут А, сторона РТ выражается на сфере как (p / 2 - В). Угол этого тр-ка при вершине К можем определить как (p - А – d A), так как азимут геод. линии в т. К равен (A + dA).
Применяя теорему косинуса угла для решения сферического тр-ка РТК, имеем
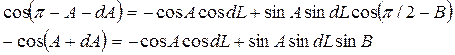
Применяя ф-лу для косинуса суммы и разлагая синусы и косинусы бескон. малых аргументов в ряд и ограничиваясь первыми членами разложений, получим дифф-ное ур-ние
,
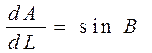в к-ром выражаем dL из второго ур-ния (4. 38) в ф-ции dA и запишем с-му трех дифф-ных ур-ний для геодез. линии элл-да в виде
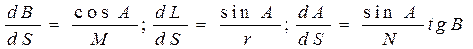(4. 39)