Основным видом построений в ГГС явл. треуг. триангуляции и трилатерации. Для того, чтобы использовать их для передачи коорд. от исходных к опред-мым пунктам необх. знать длины их сторон и внутренние углы. В проц.предварительных вычислений вводят поправки в измер. углы (в трианг.) и длины сторон (в трилат.) за редуцирование с физ. пов-ти З. на пов-ть элл-да. В рез-те получают сфероидические треуг., сторонами к-рых служат геодез. линии элл-да.
Возникает необх-ть решения этих тр-ков. При этом в триангуляции по измер. углам и длине одной из сторон тр-ка вычисляют стороны всех тр-ков сети. В трилатерации – по измер. длинам сторон вычисляют углы тр-ков. Проблема решения этой задачи закл-ся в том, что не сущ. ф-л сфероидической тригонометрии, подобных ф-лам плоской и сферической тригонометрии. Вместе с тем замечаем: во – первых, полярное сжатие земного элл-да величина малая, во – вторых, длины сторон сфероидических тр-ков – малые величины по ср. с радиусом кривизны элл-да.
Ранее мы получили выражение для ср. радиуса кривизны элл-да R = 
. Возникает вопрос, при каких условиях для решения тр-ков можно заменить область на пов-ти элл-да соотв-й областью на пов-ти шара, если его радиус принять равным R0, вычисленным по ср. широте В0 данной области элл-да. Другими словами, когда элементы сфероидического тр-ка будут с необходимой точностью соответствовать элементам сферического тр-ка. В этом случае тр-ки можно решать как сферические. Исследования показывают, что такое возможно, если сеть тр-ков располагается в сфероидическом поясе шириной до 300 км или на удалении от параллели с широтой В0 до 150 км. В этом случае длины сторон тр-ков первого и последующих классов будут отличаться на величину, не более 0. 001 м, а углы – 0. 001//. При пониженных требованиях к необходимой точности решения тр-ков ширина пояса увеличивается, например, при точности, на порядок ниже, ширина пояса может достигать 570 км.
Решение тр-ков по ф-лам сферической тригонометрии не совсем удобно на практике, когда длины сторон нужно выражать в долях радиуса (S / R0), поэтому в геодезии применяют методы решения малых сферических тр-ков по ф-лам плоской тригонометрии, основанным на теореме Лежандра и способе аддитаментов.
Теорема Лежандра
Пусть мы имеем сферический тр-к ABC на сфере радиуса R0. Возьмем плоский тр-к A/ B/ C/ с соответственно равными сторонами (рис. 5. 1). Углы этих тр-ков, расположенные против соответственно равных сторон, не будут равны соответствующим углам сферического тр-ка.
 |
Рис. 5. 1
Применяя теорему косинуса стороны для сферического тр-ка АВС, запишем
, (5. 1)
откуда можем выразить
. (5. 2)
Стороны тр-ка малы по сравнению с радиусом R0, поэтому тригоном. ф-ции малых аргументов разложим в ряд Маклорена, в рез-те получим вместо (5. 2)
(5. 3)
Заметим, что наибольший из отброшенных членов разложений в (5. 3) будет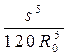 
. Поставим условие, чтобы он не превосходил величины 5*10-10, что соответствует точности вычисления углов в 0. 0001//, тогда получаем предельные длины сторон тр-ка, для к-ого (5. 3) будет обеспечивать требуемую точность 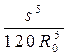£ 5*10-10, s £ R0 * 10-2 (600)1/5 » 230км. Преобразуем выражение (5. 3) с принятой точностью
Откуда несложно получить после приведения подобных членов
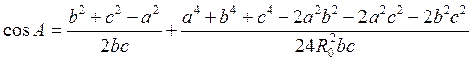. (5. 4)
Обратимся теперь к плоскому тр-ку на рис. 5. 1. Для него можем записать по теореме косинусов плоской тригонометрии
.
И выражение для sin2A = 1 – cos2A
.
С учетом этого выражение (5. 4) принимает вид
. (5. 5)
Преобразуя разность косинусов в произведение и полагая
,
получим вместо (5. 5) для разности сферического и соотв. плоского углов выражение
Несложно заметить, что ур-ние
выражает S тр-ка, поэтому для разности любых углов сферического и плоского тр-ков справедливы выражения
Поскольку сумма внутренних углов плоского тр-ка всегда равна p, можем записать для суммы углов сферического тр-ка
(5. 6)
Величина, определяющая в (5. 6) насколько сумма внутренних углов сферического тр-ка больше p, носит название сфер. избытка и обозначается e. Отсюда вывод, что сфер. избыток тр-ка прямо пропорционален площади и обратно пропорц. квадрату радиуса сферы, что и выражает теор. Лежандра. При этом каждый угол сферического тр-ка больше соотв. угла плоского тр-ка на величину одной трети сферического избытка (для n – угольника – больше на величину e / n).
Сфер. избыток может достигать в общем случае величины до 2p. Для малых тр-ков, к-рые мы рассматриваем, эта величина малая и ее выражают в секундах, поэтому ф-ла для вычисления сферического избытка имеет вид
(5. 7)
Для вычисления площади Р тр-ка можно применять любую ф-лу. Так для тр-ков триангуляции, когда известна только одна сторона удобнее ф-лы вида
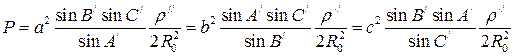(5. 8)
В трилатерации измерены длины сторон, а углы неизвестны, поэтому здесь более удобно вычислять S тр-ка по ф-ле Герона
(5. 9)
Из ф-лы (5. 7) видно, что наиб. сфер. избыток (при заданном порядке длин сторон) будет иметь равносторонний тр-к. Сфер. избыток для разл. длин сторон геодез. тр-ков не превзойдет следующих величин: при s км = 5, 10, 20, 30, 60 - e// = 0. 07, 0. 25, 1. 0, 2. 0, 8. 0 соответственно. Величина f = r// / 2R2 изменяется с широтой очень медленно. Учитывая, что сфер. избыток даже в сети 1 класса с длинами сторон до 60 км не превышает 8//, а точность вычисления углов – 0. 001//, при его вычислении достаточно удерживать 4 верные значащие цифры. Это значит, что при его вычислении можно пренебречь различием площадей сферического и плоского тр-ков, а величину f можно считать постоянной и равной для всей территории Республики Беларусь (f = 2. 530* 10 –9 ), если длины сторон выражены в метрах.