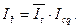Тема 5. ИНДЕКСЫ
ПЛАН:
1. Понятие об индексах и их роли в статистике.
2. Индивидуальные индексы.
3. Общие (сводные) индексы.
4. Средние индексы.
Понятие об индексах и их роли в статистике
Слово «индекс» (от лат. index) в переводе означает «указатель», «показатель», «список». В статистике под индексом понимается относительная величина (показатель), выражающая изменение сложного экономического явления во времени, в пространстве или по сравнению с эталоном (план, прогноз, норматив).
Индекс – обобщающий показатель сравнения двух сложных совокупностей, состоящих из элементов, которые непосредственно не подлежат суммированию.
Основой индексного метода при определении изменений в производстве и обращении товаров является переход от натурально-вещественной формы выражения товарных масс к стоимостным (денежным) измерителям. Именно посредством денежного выражения стоимости отдельных товаров устраняется их несравнимость как потребительских стоимостей и достигается единство.
Основным элементом индексного отношения является индексируемая величина. Под индексируемой величиной понимается значение признака статистической совокупности, изменение которой является объектом изучения. Индексы измеряются либо в виде процентов (%), либо в виде коэффициентов.
С помощью экономических индексов решаются следующие задачи:
1) измерение динамики социально-экономического явления за два и более периодов времени;
2) измерение динамики среднего экономического показателя;
3) измерение соотношения показателей по разным регионам;
4) определение степени влияния изменений значений одних показателей на динамику других;
|
|
5) пересчёт значений макроэкономических показателей из фактических цен в сопоставимые цены.
Все экономические индексы можно классифицировать по следующим признакам:
1. По степени охвата явления индексы бывают индивидуальные и общие (сводные).
1.1. Индивидуальные индексы служат для характеристики изменения отдельных элементов сложного явления.
1.2. Общие (сводные) индексы используются для измерения динамики сложного явления, составные части которого непосредственно не соизмеримы.
1.3. Групповые индексы (субиндексы) занимают промежуточное положение между индивидуальными и общими индексами, отражают закономерности в развитии отдельных частей изучаемых явлений.
2. По базе сравнения все индексы можно разделить на три группы:
2.1. Динамические (базисные и цепные) отражают изменения явлений во времени.
2.2. Индексы выполнения плана.
2.3. Территориальные применяются для межрегиональных сравнений. Большое значение эти индексы имеют в международной статистике при сопоставлении показателей социально-экономического развития различных стран.
3. По характеру объекта исследования (содержанию изучаемых объектов) общие индексы подразделяются на:
3.1. Индексы количественных показателей (индекс физического объёма продукции, работ, услуг, товарооборота).
3.2. Индексы качественных показателей (как цена, себестоимость, производительность труда, заработная плата).
В основе такого деления индексов лежит вид индексируемой величины.
4. По форме построения (методу расчёта) различаются индексы агрегатные и средние взвешенные (арифметические и гармонические).
|
|
4.1. Агрегатная форма общих индексов является основной формой экономических индексов.
4.2. Средние взвешенные (гармонические и арифметические) – это производные индексы, они получаются в результате преобразования агрегатных индексов.
5. По виду весов индексы бывают:
5.1. С постоянными весами (стандартными, отчётного периода, базисного периода).
5.2. С переменными весами.
6. По составу явления можно выделить две группы индексов:
6.1. Индексы постоянного состава.
6.2. Индексы переменного состава.
Деление индексов на эти две группы используется для анализа динамики средних показателей.
7. По периоду исчисления индексы подразделяются на годовые, квартальные, месячные, недельные.
В международной практике индексы принято обозначать символами i и I (начальная буква латинского слова index). Буквой «i » обозначаются индивидуальные (частные) индексы, буквой «I » – общие индексы.
К какому бы экономическому явлению ни относились индексы, чтобы рассчитать их, необходимо сравнивать различные уровни, которые относятся либо к различным периодам времени, либо к плановому заданию, либо к различным территориям. В связи с этим различают базисный период (период, к которому относится величина, подвергаемая сравнению) и отчётный (текущий) период (период, к которому относится сравниваемая величина). При исчислении важно правильно выбрать период, принимаемый за базу сравнения. Знак внизу справа от индекса означает период его исчисления: 0 – базисный; 1 – отчётный.
В статистике используются определённые символы для обозначения индексируемых показателей:
|
|
q – количество (объём) произведённой продукции (или количество проданного товара) данного вида в натуральном выражении;
р – цена единицы продукции или товара;
z – себестоимость единицы продукции;
v – выработка продукции в натуральном выражении на одного рабочего или в единицу времени;
t – затраты рабочего времени (труда) на производство единицы продукции данного вида, т. е. трудоёмкость единицы изделия;
Q=pq – общая стоимость произведённой продукции данного вида или товарооборот;
F=zq – общие затраты на производство продукции данного вида;
Т=tq – общие затраты рабочего времени (труда) на производство продукции данного вида или численность работников предприятия и т. д.;
W=q/Т – производство продукции данного вида в единицу времени или в расчёте на одного рабочего, т. е. уровень производительности труда в стоимостном выражении.
Индивидуальные индексы
К индивидуальным индексам прибегают, если исследователь не интересуется структурой изучаемого явления и количественную оценку уровня в данных условиях сравнивает с такой же конкретной величиной уровня этого явления в других условиях. Индивидуальный индекс характеризует динамику уровня изучаемого явления во времени за два сравниваемых периода или выражает соотношение отдельных элементов совокупности.
Так, уровень товарооборота в виде суммы выручки от продажи товара в условиях отчётного года Q1 сравнивается с аналогичной суммой выручки базисного года Q0. В итоге получаем индивидуальный индекс товарооборота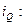 
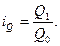
Аналогично индивидуальные индексы можно рассчитать и для любого интересующего нас показателя. В частности, поскольку сумма выручки определяется ценой товара (р) и количеством продаж в натуральном измерении (q), можно отдельно определить индивидуальные индексы цены ip и физического объёма продукции iq: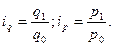 
С аналитической точки зрения iq показывает, во сколько раз увеличилась (или уменьшилась) общая сумма выручки под влиянием изменения объёма продажи в натуральных единицах. Аналогично ip показывает, во сколько раз изменилась общая сумма выручки под влиянием изменения цены товара.
Индивидуальный индекс себестоимости единицы продукции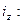 
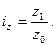
Индивидуальный индекс количества продукции, произведённой в единицу времени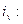 
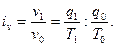
Индивидуальный индекс производительности труда по трудовым затратам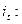 
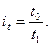
Между количеством продукции, произведённой в единицу времени, и затратами рабочего времени на производство единицы продукции существует обратная пропорциональная зависимость, т. е.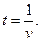 
Индивидуальный индекс выработки продукции в стоимостном выражении на одного рабочего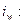 
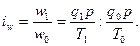
Индивидуальный индекс численности рабочих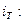 
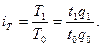
Очевидно, что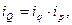 
или 
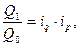откуда 
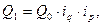где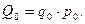 
Последняя формула представляет собой двухфакторную индексную мультипликативную модель итогового показателя, в данном случае – объёма товарооборота. Посредством такой модели находят прирост итога под влиянием каждого фактора в отдельности.
Мультипликативнойона называется потому, что содержит только действие умножения. Если в формуле только сложение, или вычитание, или оба этих действия, то она называется аддитивной моделью. Если в формуле только деление, то она называется кратной моделью. Если в формуле сложение и вычитание с умножением и делением в любом сочетании, то она называется смешанной моделью.
Так, если основываться на формуле выручки вида Q = pq, то её изменение за счёт цены, как первого фактора, будет равняться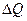 
p = (ip –1) Q0 .
Изменение выручки за счёт количества товара, как второго фактора, определится по выражению 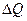q= ip(iq –1) Q0.
Суммарное по факторам изменение выручки по-прежнему равняется её общему изменению: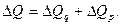 
Общие (сводные) индексы
В экономических расчётах чаще всего используются общие (сводные) индексы, которые характеризуют обобщающие результаты совместного изменения всех единиц, образующих статистическую совокупность. Основной формой общих индексов являются агрегатные индексы.
Агрегатный индекс (от лат. aggregatus – соединённый, складываемый, суммируемый) – сложный относительный показатель, который характеризует среднее изменение социально-экономического явления, состоящего из несоизмеримых элементов. Особенность этой формы индекса состоит в том, что в агрегатной форме непосредственно сравниваются две суммы одноимённых показателей.
Индексируемой величиной называется признак, изменение которого изучается (цена товаров, курс акций, затраты рабочего времени на производство продукции, количество проданных товаров и т. д.). Для преодоления разнородности и несуммарности отдельных элементов изучаемого явления в индекс вводится дополнительный неизменный показатель, тесно связанный с индексируемой величиной. Этот показатель называется весом агрегатного индекса, или показателем сопряжения. Вес индекса– это величина, служащая для целей соизмерения индексируемых величин в сложных статистических совокупностях, поэтому веса индекса называют ещё соизмерителями. Они необходимы для перехода от натуральных измерителей разнородных единиц статистической совокупности к однородным показателям. При этом в числителе и знаменателе общего индекса изменяется лишь значение индексируемой величины, а их соизмерители являются постоянными величинами. В качестве соизмерителей индексируемых величин выступают тесно связанные с ними экономические показатели: цены, количество продукции и др. Так, если индексируются цены, то для того, чтобы преодолеть несуммарность цен, цены умножают на количество. Произведение каждой индексируемой величины на соизмеритель образует в индексном отношении определённые экономические категории (товарооборот).
Правила определения весов общих индексов:
1). Если индексируемой величиной является качественный признак, то вес принимается на уровне текущего периода, по отчётным данным.
2). Если же индексируемой величиной является количественный признак, то вес принимается на уровне базисного периода.
1. Агрегатный индекс физического объёма товарооборота
(формула, предложенная немецким статистиком Этьеном Ласпейресом в 1864 году):
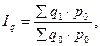
где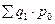 
– условная стоимость товаров, реализованных в отчётном периоде по ценам базисного периода;
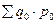– размер товарооборота в базисном периоде.
Индекс физического объёма показывает, как за счёт изменения количества реализованной продукции изменяется размер товарооборота в отчётном периоде по сравнению с базисным.
Поскольку в числителе формулы индекса Ласпейреса содержится сумма стоимости реализации товаров в текущем периоде по неизменным (базисным) ценам, а в знаменателе – сумма фактической стоимости товаров, реализованных в базисном периоде в тех же неизменных (базисных) ценах, то данный индекс является агрегатным индексом товарооборота в сопоставимых (базисных) ценах.
При построении индекса физического объёма продукции в качестве соизмерителей (весов) принимаются не только сопоставимые, неизменные, фиксированные цены, отличающиеся от текущих (действующих) цен (в условиях инфляции это могут быть цены предшествующего периода), но и себестоимость продукции z 0. В последнем случае индекс будет характеризовать изменение издержек производства:
.
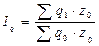2. Агрегатный индекс цен
(формула, предложенная немецким статистиком Германом Пааше в 1874 году):
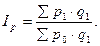
Индекс цен Пааше показывает изменение цен отчётного периода по сравнению с базисным (на сколько товары стали дороже (дешевле)). Тем самым определяется величина фактической экономии при условии, что товары были бы реализованы в отчётном периоде по базисным ценам.
В целом общий индекс цены показывает, на сколько процентов изменился размер товарооборота в отчётном периоде по сравнению с базисным за счёт изменения индивидуальных цен. Индексы цен широко используются в экономических расчётах для отражения динамики инфляционных процессов и для пересчёта важнейших показателей системы национальных счетов из фактических цен в сопоставимые цены.
3. Агрегатный индекс общего объёма товарооборота (стоимости продукции):
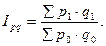
Общий индекс товарооборота показывает, на сколько процентов изменяется товарооборот в отчётном периоде по сравнению с базисным при влиянии двух факторов: и цены, и физического объёма продукции.
Многие экономические индексы тесно связаны между собой и образуют индексные системы. Между индексом цены, индексом физического объёма и индексом товарооборота существует взаимосвязь:
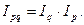
Произведение индекса цен на индекс физического объёма товарооборота или продукции даёт индекс физического объёма товарооборота в фактических ценах, или индекс стоимости продукции. При этом входящие в эту двухфакторную импликативную модель индексы физического объёма и цен должны выражаться по разным формулам: один – по Ласпейресу, другой – по Пааше.
Данная модель используется для определения абсолютного прироста стоимости продукции, обусловленной влиянием двух факторов: изменения физического объёма продукции (q) и изменения уровня цен на продукцию (p):
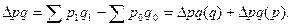
Дальнейший расчёт величин составляющих формулу факторных приростов может осуществляться двояким образом:
1). Если принимается предположение об очерёдности влияния факторов – сначала q, а затем р, – то общий прирост товарооборота будет распределяться по факторам следующим образом:
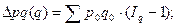
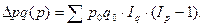
2). Если же принимается предположение об обратной последовательности влияния факторов – сначала р, затем q, – то меняются и формулы разложения прироста и формулы расчёта индексов Iq и Ip. Тогда:
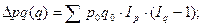
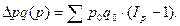
Индекс себестоимости промышленной продукции связан с индексом физического объёма продукции по себестоимости, образуя следующую индексную систему:
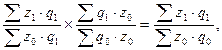или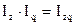 
.
Произведение индекса себестоимости продукции на индекс физического объёма даёт индекс затрат в производстве.
Используя индексные системы, можно по двум известным индексам найти третий, неизвестный.
При использовании агрегатных индексов придерживаются следующих правил:
1) при расчёте индексов количественных показателей соизмерители принимаются на уровне базисного периода, т. е. расчёт ведётся по формуле Ласпейреса;
2) при расчёте индексов качественных показателей веса фиксируются на уровне, относящемся к текущему периоду, т. е. используется формула Пааше.
Средние индексы
Средний индекс – это индекс, вычисленный как средняя величина из индивидуальных индексов.
Поскольку существует несколько форм (видов) средних величин, то при расчёте средних индексов прежде всего возникает вопрос о форме средней и о весах. В статистической практике средние индексы рассчитываются на основе агрегатных индексов преимущественно в форме среднего арифметического и среднего гармонического индексов.
Всякий агрегатный индекс может быть преобразован в средний арифметический из индивидуальных индексов. Для этого индексируемая величина отчётного периода, стоящая в числителе агрегатного индекса, заменяется произведением индивидуального индекса на индексируемую величину базисного периода.
Средний арифметический индекс физического объёма используется, если неизвестны данные о физическом объёме в отчётном периоде, в таком случае физический объём отчётного периода рассчитывают исходя из индивидуального индекса физического объёма.
Индивидуальный индекс физического объёма продукции (товарооборота) равен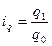 
, откуда 
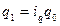, следовательно, преобразование агрегатного индекса в средний арифметический принимает вид:
= 
= 
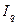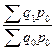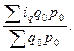
Аналогично индивидуальный индекс цен равен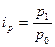 
, откуда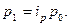 
Средний арифметический индекс цен:
= 
= 
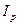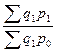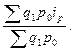
Аналогично индивидуальный индекс себестоимости равен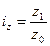 
, откуда 
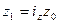, следовательно, средний арифметический индекс себестоимости:
= 
= 
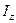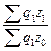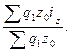
Средний арифметический индекс производительности труда:
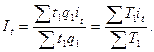
Для анализа производительности труда чаще используется индекс Станислава Густавовича Струмилина:
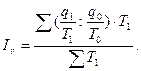
Средний гармонический индекс физического объёма используется для аналитических оценок в случае, когда неизвестно q 0, но дано значение q 1 и индивидуальный индекс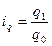 
(откуда 
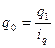), а также стоимость продукции базисного периода p 0:
.
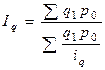Средний гармонический индекс цены определяется из преобразования агрегатного индекса цены, учитывая, что цена базисного периода определяется через индивидуальный индекс цены (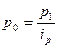
):
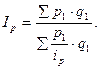
Средний гармонический индекс себестоимости:
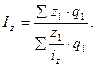
При определении среднего гармонического индекса цен весами является стоимость продукции текущего периода, а при определении среднего гармонического индекса себестоимости – издержки производства.
“Идеальный” индекс цен Ирвинга Фишера, предложенный в начале ХХ века, рассчитывается как средняя геометрическая индексов цен Пааше и Ласпейреса:
.
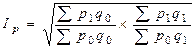Этот индекс Фишер назвал «идеальным»,поскольку в нём не отдаётся предпочтение ни продукции базисного периода, ни продукции текущего периода.
Индекс цен Фишера “обратим” во времени (т. е. при перестановке базисного и отчётного периода местами получается индекс, равный обратной величине первоначального индекса), но лишён конкретного экономического содержания.
Вместе с тем, проведённые В. Ф. Ворониным многочисленные расчёты показали, что для целей статистики вполне можно применять не среднюю геометрическую, а простую среднюю арифметическую величину из индексов Ласпейреса и Пааше, определяя её по формулам:
- для количества товаров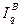 
= 
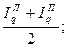
- для цен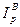 
= 
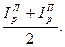
При синтезировании общего индекса цен вместо фактического количества товаров (в отчётный и базисный периоды) в качестве соизмерителей индексируемых величин р 1 и р 0 могут применяться средние величины реализации товаров. При таком способе расчёта формула сводного индекса цен (называемого индексом цен Лоу) выглядит следующим образом:
.
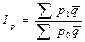Индекс цен Лоу применяется в расчётах при закупках или реализации товаров в течение продолжительных периодов времени (пятилетках, десятилетиях и т. п.), поскольку он даёт возможность анализа цен с учётом происходящих внутри отдельных субпериодов изменений в ассортиментном составе товаров.
Средние индексы широко используются для анализа рынка ценных бумаг. Наиболее известным из них является Промышленный индекс Доу-Джонса (Dow Jones Industrial Average Index). Этот индекс был предложен и опубликован в 1896 году американским бизнесменом и основателем крупнейшей для делового мира газеты «The Wall Street Journal» Чарльзом Доу (1851 – 1902). Он представляет собой средний арифметический индекс значений курсов акций ведущих американских компаний, котирующихся на Нью-Йоркской фондовой бирже. С 1928 года рассчитывается по 30 компаний, список который постоянно ротируется. В качестве базового выбран 1920 год. Индекс Стэндарда и Пура (Standard and Poor’s 500 Stock Index) – фондовый индекс, представляющий собой средний взвешенный показатель, рассчитываемый по курсам акций 500 компаний США, имеющих наибольшую капитализацию.
При изучении качественных показателей часто приходится рассматривать изменение во времени (или пространстве) средней величины индексируемого показателя для определённой совокупности. Динамику среднего показателя можно отразить как за счёт изменения самой индексируемой величины и её веса, так и за счёт каждого из этих двух факторов отдельно.
Индекс постоянного (фиксированного) состава по своей форме тождественен агрегатному индексу и отражает динамику среднего показателя лишь за счёт изменения индексируемой величины, при фиксировании весов на уровне, как правило, отчётного периода.
Он показывает изменение общей средней цены за счёт изменения индивидуальных цен в отчётном периоде по сравнению с базисным:
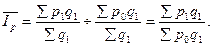
Другими словами, индекс фиксированного состава исключает влияние изменения структуры (состава) совокупности на динамику средних величин, т. е. он характеризует динамику средних величин, рассчитанных для двух периодов при одной и той же фиксированной структуре.
Индекс переменного состава отражает динамику среднего показателя (для однородной совокупности) как за счёт изменения индексируемой величины у отдельных элементов (частей целого), так и за счёт изменения весов, по которым взвешиваются отдельные значения этой величины. Любой индекс переменного состава – это отношение двух средних величин для однородной совокупности (за два периода или по двум территориям). К такому типу индексов относится индекс средней цены, который показывает, на сколько процентов средняя цена (определяемая по формуле средней арифметической взвешенной) изменяется в отчётном периоде по сравнению с базисным:
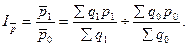
Индекс структурных сдвигов показывает динамику среднего показателя лишь за счёт изменения весов индекса, отражающих структуру изучаемого явления, при фиксировании индексируемой величины на уровне базисного периода. Он показывает изменение средней цены за счёт изменения физического объёма:
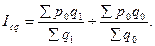
Экономическая сущность индекса структурных изменений состоит в том, что он показывает, во сколько раз изменился общий средний уровень только за счёт изменения удельного веса каждого объекта в общем объёме количественного признака. В той же мере индекс структурных изменений показывает влияние процессов перераспределения на общий прирост итогового показателя.
Если от абсолютных весов перейти к относительным (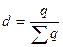
и Σ d =1), формулы индексов динамики средних величин примут вид:
а) индекс фиксированного состава: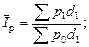 
б) индекс переменного состава: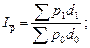 
в) индекс структурных сдвигов: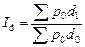 
.
Исходя из вышеизложенных формул, можно определить абсолютный прирост (уменьшение) среднего уровня признака в целом по совокупности и за счёт отдельных факторов.
Очевидно, что между трёмя указанными индексами существует тесная взаимосвязь. Индекс переменного состава равен произведению индекса постоянного состава на индекс структурных сдвигов:
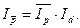
Индекс структурных сдвигов используется также для построения трёхфакторной импликативной модели определения общего индекса товарооборота:
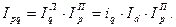
Трёхфакторная модель возможна к широкому применению в экономическом анализе для установления количественного влияния каждого фактора на вариацию сложного явления.
Подставляя значение индекса товарооборота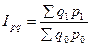 
в полученную формулу импликативной модели, получаем:
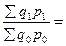
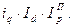
Отсюда можно найти общую выручку отчётного периода:
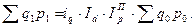
Агрегатный индекс товарооборота может быть рассчитан ещё двумя способами, учитывая взаимосвязь индексов динамики:
а) через индекс постоянного состава: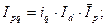 
б) через индекс переменного состава: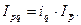 
Следовательно, общий индекс выручки от реализации есть произведение индивидуального индекса количества товаров и индекса переменного состава.
Результат расчёта любым способом должен быть одинаковым и это яркий пример того, что истина всегда одна, хотя пути её достижения могут быть разными.
Пример 1.
Имеются данные о продаже мяса на двух рынках города:
| Рынок | Цена за 1 кг, руб. | Продано, кг | ||
| Базисный период, p0 | Отчётный период, p1 | Базисный период, q0 | Отчётный период, q1 | |
Определить:
1) индивидуальные индексы: цен; физического объёма;
2) общие агрегатные индексы: цен; физического объёма; товарооборота.
Решение:
1). Индивидуальные индексы цен:
а) для рынка 1: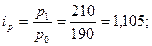 
б) для рынка 2: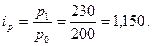 
2). Индивидуальные индексы физического объёма товарооборота:
а) для рынка 1: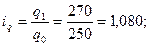 
б) для рынка 2: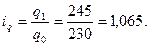 
3). Агрегатный индекс цен по формуле Пааше:
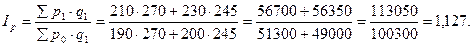
4). Агрегатный индекс физического объёма товарооборота по формуле Ласпейреса:
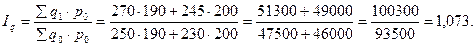
5). Агрегатный индекс товарооборота:
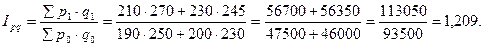
Проверка правильности расчётов по импликативной модели:
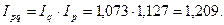
6). Общее изменение товарооборота:
∆pq= 113050 – 93500 = 19550 руб.
Изменение товарооборота за счёт цены:
∆pq(p) = 113050 – 100300 = 12750 руб.
Изменение товарооборота за счёт объёма продаж:
∆pq(q) = 100300 – 93500 = 6800 руб.
Проверка правильности расчёта: 19550 = 12750 + 6800.
Пример 2.
Имеются следующие данные о выпуске продукции и затратах на её производство в условиях новой и старой технологии:
| Технология | Количество выпущенной продукции, тыс. шт. | Затраты времени на изготовление единицы продукции, ч. | ||
| Базисный период | Отчётный период | Базисный период | Отчётный период | |
| Старая | 4,0 | 3,9 | ||
| Новая | 2,0 | 1,8 |
Определить индексы постоянного и переменного состава, индекс влияния структурных сдвигов на изменение средних затрат времени.
Решение:
Индекс постоянного состава:
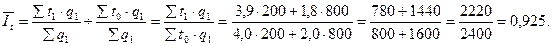
Индекс переменного состава:
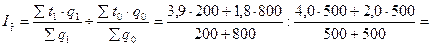
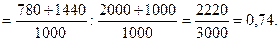
Индекс влияния структурных сдвигов:
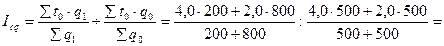
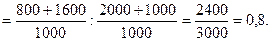
Проверка правильности выполненных расчётов:
