Кинематика и динамика
1. Мгновенной скоростью при криволинейном неравномерном движении называют (производную радиус- вектора по времени)
2. За один оборот колеса радиуса R, которое катится по плоскости вдоль прямой линии, модуль перемещения одной из точек равен (2πR)
3. Расстояние между двумя городами автобус проехал со скоростью 10м/с, а обратный путь со скоростью 15м/с. Средняя скорость автобуса на всём пути равна (12м/с)
4. Материальная точка движется вдоль оси х. Координата точки задается формулой х=8-5t-t 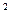 .Зависимость проекции скорости точки от времени имеет вид (v=-5-2t)
.Зависимость проекции скорости точки от времени имеет вид (v=-5-2t)
5. Материальная точка движется вдоль оси х по закону х=3-t+10t 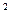 м. Проекция ускорения точки на ось х равна (20м/с
м. Проекция ускорения точки на ось х равна (20м/с  )
)
6. Компоненты ускорения равны (вторым производным соответствующих координат по времени)
7. Модуль ускорения характеризует быстроту измерения (скорости)
8. Точка движется по спирали от периферии к центру с постоянной по модулю скоростью. Как при этом изменяются ее тангенциальное и нормальное ускорения (а(т) не изменяется, а(н) увеличивается)
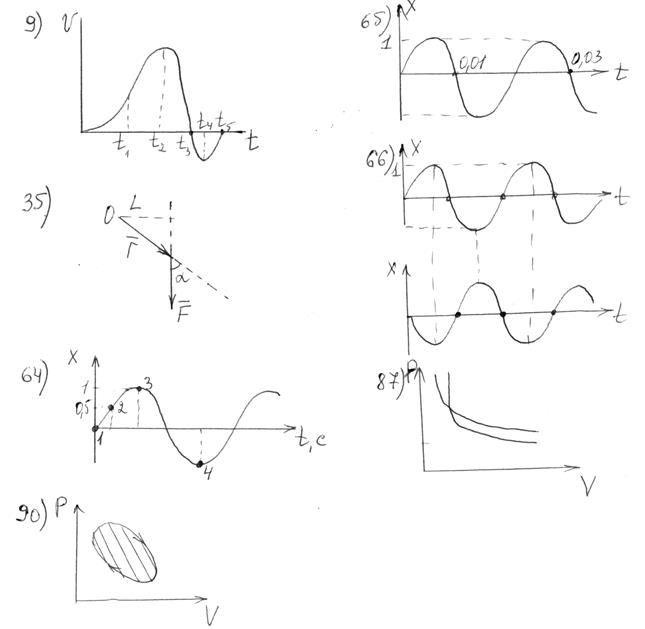
9. На рисунке приведен график скорости прямолинейного неравномерного движения. В какой момент времени тело имеет максимальное ускорение? Максимальную скорость? Максимальную координату? (t1, t2, t3)
10. Если центростремительное ускорение точки на ободе вращающегося колеса возрастает в 4 раза, то линейная скорость этой точки возрастает в (2 раза)
11. При угловом ускорении вращающегося тела равном 5 рад/с 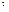 , модуль тангенциального ускорения точки тела на расстоянии 10 см от оси вращения равен (0,5 м/ с
, модуль тангенциального ускорения точки тела на расстоянии 10 см от оси вращения равен (0,5 м/ с  )
)
12. Инерциальной системой отсчета называют такую систему, в которой тела не подверженные воздействию других тел движутся (равномерно и прямолинейно)
13. Какая из перечисленных физических величин имеет размерность 
 (момент силы)
(момент силы)
14. Какая из перечисленных физических величин имеет размерность 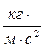
 (давление)
(давление)
15. Согласно второму закону Ньютона равнодействующая всех сил действующих на частицу равна (скорости изменения импульса)
16. Согласно третьему закону Ньютона два тела действуют друг на друга с силами (равными по модулю и противоположными по направлению. Силы приложены к разным телам)
17. При замедленном движении тела, массой m, вертикально вниз с ускорением а модуль силы F действующей на горизонтальную опору или подвес равен (P=m(g+a))
18. Тело массой 1кг лежит на горизонтальной поверхности. Коэффициент трения =0,1. g=10м/ с  . Сила трения действующая на тело равна (1Н)
. Сила трения действующая на тело равна (1Н)
19. Зависимость потенциальной энергии от его положения изображается параболой, удовлетворяющей уравнению W=ax 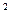 .При этом сила действующая на тело изменяется по закону (F=-2ax)
.При этом сила действующая на тело изменяется по закону (F=-2ax)
20. Какая из перечисленных сил является неконсервативной (сила трения)
21. Какая из перечисленных сил является диссипативной (сила сопротивления)
22. Сумма внутренних сил действующих между телами механической системы (равно нулю)
23. Мощность это (работа, совершаемая в единицу времени)
24. Вектор силы, действующий на тело составляет с вектором скорости движения угол α>π/2. При этом работа, совершаемая силой (А<0)
Неинерциальные системы отсчета
25. Сила Карнолиса (не совершает работу над частицей, но изменяет направление её скорости относительно диска)
26. Если скорость вращения системы отсчета увеличить в n раз, то модуль центробежной силы (увеличится в n 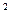 раз)
раз)
27. При изменении угловой скорости вращающейся системы отсчета в 3 раза, центробежная сила (увеличится в 9 раз)
Гравитация
28. Как изменится напряженность гравитационного поля при подъеме с поверхности земли на высоту равную диаметру земли. Вращение земли не учитывать (уменьшится в 9 раз)
29. Как связаны напряженность и потенциал гравитационного поля земли (напряженность гравитационного поля равна градиенту потенциала, взятого с обратным знаком) Законы сохранения
30. Какова связь между кинетической энергией материальной точки и работой приложенных к точке сил (работа равна приращению кинетической энергии материальной точки)
31. Суммарный импульс системы материальных точек остается постоянным в (замкнутой механической системе)
32. Стальной шарик массы m падает на стальную плитку с высоты h1 и отскакивает от неё на высоту h2=h1. За время удара плитка получает импульс силы равный ( )
)
33. В основе закона сохранения энергии лежит (однородность времени)
34. Для системы материальных точек, находящихся под действием консервативных и неконсервативных сил, полная механическая энергия (не сохраняется)
35. Момент силы относительно (.) О это вектор, точка приложения которого (совпадает с (.) О, а направление перпендикулярно вектору F и r за чертеж)
36. Момент импульса L материальной точки относительно (.) О определяется следующим соотношением массы m, скорости v и радиус- вектора r ([r, mv])
37. При равноускоренном движении материальной точки по окружности для вектора момента импульса справедливо утверждение (модуль момента импульса увеличивается, а направление остается постоянным)
38. Частные производные потенциальной энергии по направлениям декартовой системы координат x,y,z взятые с обратным знаком являются (компонентами консервативной силы по осям координат)
39. Кинетическая энергия движущегося со скоростью v тела пропорциональна (квадрату скорости) Соударение тел
40. При абсолютно упругом ударе тела разлетаются со скоростями определяемыми (законами сохранения полной механической энергии и импульса)
41. Шары равной массы имеющие скорости v1 и v2 до удара, после абсолютно упругого центрального соударения имеют скорости u1 и u2, которые равны (u1=v2, u2=v1) Механика твердого тела
42. Шар, диск и цилиндр одинаковой массы и радиуса скатываются с наклонной плоскости высотой h. При этом кинетическая энергия (шара меньше, чем диска и цилиндра)
43. Центр масс системы материальных точек r, где mi, ri –масса и радиус- вектор i-ой материальной точки, m- масса всех материальных точек системы определяется следующей формой (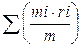 )
)
44. Центр масс изолированной инерциальной системы материальных точек движется (с ускорением а=0)
45. Момент инерции тела равен (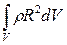 )
)
46. Момент инерции I равен 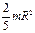 для (шара)
для (шара)
47. Кинетическая энергия тела массой m катящегося с линейной скоростью V определяется формулой (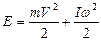 )
)
48.При уменьшении скорости вращения гироскопа вокруг оси угловая скорость прецессии (увеличивается пропорционально этой скорости)
Механика жидкости
48. Жидкость называется несжимаемой если всюду одинакова (её плотность)
49. При течении несжимаемой жидкости со скоростью V, динамическое давление пропорционально (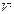 )
) 
50. Стационарное течение несжимаемой и идеальной жидкости вдоль любой линии тока описывает уравнение (Бернулли)
51. Формула Пуазейля справедлива для течения жидкости в трубах при режиме течения (ламинарном)
52. Профили скорости при ламинарном и турбулентном течении жидкости в круглой трубе (параболический и плоский)
53. Какая из перечисленных величин имеет размерность м 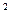 /с (кинематическая вязкость) Элементы специальной теории относительности
/с (кинематическая вязкость) Элементы специальной теории относительности
54. Прямые преобразования Галилея (х=х’+vt; y=y’; z=z’; t=t’)
55. В соответствии с принципом относительности Галилея законы ньютоновской кинетической механики (во всех инерциальных системах отсчета одинаковы)
56. Преобразования Галилея верны когда имеем дело со скоростями (существенно меньшими, чем скорость света в вакууме)
57. Преобразования Лоренца это (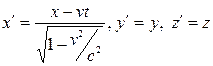 ) если x y z v t – координаты, скорость и время в покоящейся системе отсчета, а со штрихами- в системе отсчета движущейся относительно покоящейся инерциальной системы отсчета.
) если x y z v t – координаты, скорость и время в покоящейся системе отсчета, а со штрихами- в системе отсчета движущейся относительно покоящейся инерциальной системы отсчета.
58. Из преобразований Лоренца следует, что продольная длина (не является неизменной величиной, не существует абсолютной одновременности)
59. Собственное время это время (отсчитываемое по часам, движущимся вместе с телом отсчета. Собственное время самое длинное)
60. В релятивистской динамике масса (возрастает с увеличением скорости. Релятивистский импульс увеличивается)
61. В релятивистской динамике полная энергия определяется, если m- масса покоя (E=mc 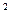 ) Колебания материальной точки
) Колебания материальной точки
62. Если период синусоидальной внешней силы приближается к периоду собственных колебаний, то (амплитуда возрастает. Это явление названо резонансом)
63. На графике представлена временная зависимость смещения некоторой материальной точки из положения равновесия при гармонических колебаниях. Чему равняются фазы колебаний соответственно в точках 1,2,3,4 (0; π/6 рад; π/2 рад; 3π/2 рад)
64. Чему равна амплитуда колебаний, период колебаний и частота (1м, 0,02с, 50Гц)
65. Чему равна разность фаз колебаний первого и второго колебания и частота колебаний (π рад, 5Гц)
66. Точка совершает колебательное движение по уравнениям 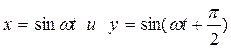 . По какой траектории движется точка (точка движется описывая восьмерку, с длинной осью y)
. По какой траектории движется точка (точка движется описывая восьмерку, с длинной осью y)
67. При затухающих колебаниях амплитуда колебаний спустя два периода после начала колебаний, уменьшается в 2 раза. Во сколько раз уменьшится энергия колебаний (в 4 раза)
68. Материальная точка совершает колебания в соответствии с соотношением x=0,1sin(10t+π/2)м. Какова скорость движения точки в момент времени t=0 (0м/с)
69. При сложении колебаний с одинаковыми амплитудами и близкими частотами одного направления, чем меньше разность частот, тем (меньше частота биений, больше максимальная амплитуда)
70. Материальная точка совершает колебания в соответствии с уравнением x=0,01sin(10t+π). Какова скорость движения точек в момент времени t=0 (0,1м/с) Пружинный, математический и физический маятник
71. Как изменится период колебаний груза на пружине, если жесткость пружины уменьшится в 16 раз (увеличится в 4 раза)
72. Как изменится период колебаний пружинного маятника при увеличении массы груза в 2 раза (возрастет в 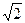 раз)
раз)
73. Как изменится частота колебаний пружинного маятника при увеличении жесткости пружины в 4 раза (возрастет в 2 раза)
74. Ускорение свободного падения на Луне в 6 раз меньше на Земле. Во сколько раз отличаются периоды колебаний маятника, если вначале они измерятся на Земле, а затем на Луне (в 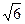 раз больше)
раз больше)
75. Два математических маятника имеют длины, отличающиеся в 9 раз. Во сколько раз частота колебаний маятника с большей длиной отличается от маятника с меньшей (в 3 раза меньше)
76. Период колебаний математического маятника вблизи поверхности Земли (прямо пропорционален корню квадратному из длины маятника и обратно пропорционален корню квадратному из величины ускорения свободного падения, от массы не зависит)
77. Тонкий однородный стержень отклонили на малый угол и отпустили, в результате чего начались свободные колебания стержня. При каких условиях период колебания стержня наибольший (чем больше длина и масса стержня) Волновые процессы
78. Звуковые волны это (упругие или механические волны с частотами от 16 до 2*10 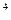 Гц)
Гц)
79. Скорость звука в воздухе тем больше, чем (выше температура, независимо от давления)
80. Плоская волна отражается от плоскости, падая на нее нормально. Амплитуда волн, посылаемых источником Ао. Какая амплитуда А стоячей волны будет наблюдаться в пучностях (А=2Ао)
81. Плоская волна длиной λ набегает на плоскую преграду, от которой отражается, меняя фазу. На каком расстоянии от преграды (ℓ1 и ℓ2) образуются в стоячей волне ближайший к преграде узел и ближайшая к преграде пучность (ℓ1= ℓ2=) Основы молекулярной физики и термодинамики
82. Атомная масса химического элемента это (отношение массы атома этого элемента к 1/12 массы атома углерода)
83. Удельной теплоемкостью тела называется количество теплоты, необходимое для нагревания (единицы массы тела на 1 К)
84. К термодинамическим параметрам системы относятся (температура, давление и объем)
85. Адиабатным называют процесс в термодинамической системе, если он не сопровождается (теплообменом с окружающей средой)
86. График для изотермы с адиабатой
87. Распространение звука в газах при нормальных условиях рассматривают как (адиабатный процесс)
88. Первый закон термодинамики: количество теплоты, сообщенное системе, идет на (увеличение её внутренней энергии и совершение работы против внешних сил)
89. Где правильно обозначена работа над телом при изменении объема в термодинамическом цикле
90. При хаотичном движении молекул идеального газа внутри кубического объема об единичную площадку поверхности этого объема в единицу времени ударяется (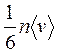 молекул) n- общее число молекул, v- средняя скорость
молекул) n- общее число молекул, v- средняя скорость
91. Числом степеней свободы механической системы называется количество (независимых величин, с помощью которых может быть задано положение системы в пространстве)
92. Согласно закону равнораспределения на каждую степень свободы молекулы, приходится в среднем одинаковая кинетическая энергия, равная (1/2kT)
93. Отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме зависит от числа степеней свободы молекулы идеального газа как (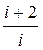 )
)
94. Из закона распределения Больцмана следует, что молекулы располагаются большей концентрацией там, где (больше их потенциальная энергия)
95. Политропическим процессом называют процесс проходящий при (постоянном значении показателя политропы)
96. Из второго начала термодинамики следует что (энтропия изолированной термодинамической системы может возрастать или оставаться постоянной)
97. При стремлении температуры к абсолютному нулю энтропия всякого тела (стремится к нулю)
98. Теорема Барно: коэффициент полезного действия всех обратимых машин, работающих в идентичных условиях одинаков и (определяется только температурами нагревателя и холодильника)
99. Тройная точка на фазовой диаграмме, точка в которой (могут находится в равновесии газообразная, твердая и жидкая фазы)