Типовые контрольные работы
По дискретной математике.
ТЕМА 1. Алгебра высказываний.
Задание 1. Проверить с помощью таблицы истинности, является
Ли данная формула тавтологией.
Вариант 1.

Вариант 2.
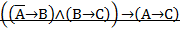
Вариант 3.

Вариант 4.

Вариант 5.
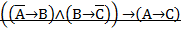
Вариант 6.
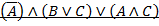
Вариант 7.
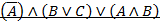
Вариант 8.

Вариант 9.

Вариант 10.

Задание 2. Проверить с помощью равносильных преобразований является ли формула из Задания 1 тавтологией.
Задание 3. Решить уравнение(найти одно из возможных решений, если такие имеются).
Вариант 1.
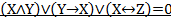
Вариант 2.
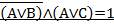
Вариант 3.
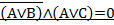
Вариант 4.
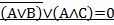
Вариант 5.
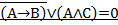
Вариант 6.
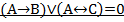
Вариант 7.
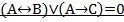
Вариант 8.
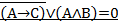
Вариант 9.
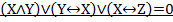
Вариант 10.

Задание 4. Построить СДНФ для данной функции.
Вариант 1.
⌐ (X/\ Y)→ ⌐ (X\/Z)
Вариант 2.
(X↔Z)→(X/\ ⌐ Y)
Вариант 3.
(X↔Y) /\ (⌐ Z → (T/\ ⌐ X))
Вариант 4.
((X\/Y)→Z) ↔ ⌐ X
Вариант 5.
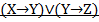
Вариант 6.
(X/\ Y) \/Z
Вариант 7.
(⌐ Z → ⌐ Y) → ((X/\ ⌐ Z) /\ Y)
Вариант 8.
(X ↔ Y)∨ (⌐ Y ∧ Z)
Вариант 9.
(⌐Y ∧ X)∨ (Z ↔ Y)
Вариант 10.
(⌐X → Z)→Y)→ X
Задание 6. Построить СКНФ для данной функции.
Вариант 1.

Вариант 2.

Вариант 3.
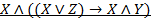
Вариант 4.
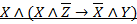
Вариант 5.

Вариант 6.
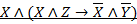
Вариант 7.
((⌐X ↔Y) ∨ Z) ∧⌐Y
Вариант 8.
(Y ↔ X)→(Y ∧ ⌐Z)
Вариант 9.
((⌐X → Z)→Y)→ X
Вариант 10.
(X ∧ Z) ∨ (⌐Y ↔ Z)
Тема 2. Множества.
Задание 1. Доказать тождества, используя основные теоремы и аксиомы алгебры множеств или с помощью диаграмм Эйлера-Венна.
Вариант 1.
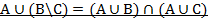
Вариант 2.

Вариант 3.
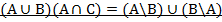
Вариант 4.
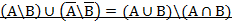
Вариант 5.
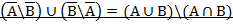
Вариант 6.
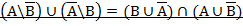
Вариант 7.

Вариант 8.
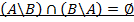
Вариант 9.
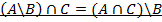
Вариант 10.
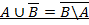
Задание 2.
1. Установить биекцию между полуинтервалом (0,1] и интервалом (2,7).
2. Установить биекцию между множеством рациональных чисел отрезка [ a, b ] и множеством рациональных чисел отрезка [ c, d ], где a, b, c, d – рациональные числа.
3. Установить биекцию между множеством рациональных чисел отрезка [0, 1] и множеством рациональных чисел больших числа 2.
4. Установить биекцию между множеством точек прямой и множеством точек полуокружности.
5. Установить биекцию между множеством точек произвольной окружности и множеством точек прямой.
6. Установить биекцию между множеством точек замкнутого круга и множеством точек открытого круга.
7. Установить биекцию между множеством точек окружности и множеством точек круга.
8. Указать биекцию между точками куба и ребром куба.
9. Установить биекцию между точками плоскости R 2 и точками полуплоскости y ³ 0.
10. Установить биекцию между точками открытого круга и точками дополнения к его замыканию.
Задание 3. Решите задачу.
| Номер варианта. | Задача |
| В классе 32 учащихся. Из них 18 посещают химический кружок, 12 – биологический, 8 учеников не посещают ни одного их этих кружков. Сколько учеников посещают и химический и биологический кружки? | |
| В классе 32 учащихся. Из них 18 посещают химический кружок, 12 – биологический, 8 учеников не посещают ни одного их этих кружков. Сколько учеников посещают только химический кружок? | |
| Все студенты первого курса КГТУ специальности «ИС» изучают 3 языка программирования. В этом году 19 студентов предпочли изучать Pascal, 14 выбрали Basic, а 17 решили заниматься Delphi. Кроме того, было 4 студента, слушающих курс по Pascal и Basic, трое изучают Pascal и Delphi, трое – Delphi и Basic. Известно, что никто из студентов не отважился посещать сразу 3 курса. Сколько студентов в группе «ИС»? | |
| Все студенты первого курса КГТУ специальности «ИС» изучают 3 языка программирования. В этом году 19 студентов предпочли изучать Pascal, 14 выбрали Basic, а 17 решили заниматься Delphi. Кроме того, было 4 студента, слушающих курс по Pascal и Basic, трое изучают Pascal и Delphi, трое – Delphi и Basic. Известно, что никто из студентов не отважился посещать сразу 3 курса. Сколько из них были увлечены только Delphi? | |
| Опрошено 200 аквариумистов, 85 из них разводят дома сомов, 95 предпочитают гуппи, 100 – золотых рыбок, 26 – сомов и золотых рыбок, 22 – гуппи и золотых рыбок, 17 – сомов и гуппи, 5 опрошенных любуются в своем аквариуме на все три вида рыбок. Сколько аквариумистов держат в своем аквариуме сомов, но не имеют гуппи? | |
| Опрошено 200 аквариумистов, 85 из них разводят дома сомов, 95 предпочитают гуппи, 100 – золотых рыбок, 26 – сомов и золотых рыбок, 22 – гуппи и золотых рыбок, 17 – сомов и гуппи, 5 опрошенных любуются в своем аквариуме на все три вида рыбок. Сколько аквариумистов держат в своем аквариуме сомов или гуппи, но не любят золотых рыбок? | |
| Среди счастливчиков, кому повезло поймать золотую рыбку, пожелавших новую квартиру оказалось 18 человек, дорогую машину – 14, хорошую работу – 28, квартиру и машину – 5, квартиру и работу – 10, машину и работу – 8, все три желания загадало 3 человека. Сколько всего человек поймали золотую рыбку? Сколько среди них загадавших только одно желание? | |
| В лыжной, хоккейной и конькобежной секциях 38 студентов потока. Известно, что в лыжной секции занимается 21 студент, среди которых 3 студента занимались еще в конькобежной секции, 6 студента еще в хоккейной секции и один студент занимался одновременно во всех трех секциях. В конькобежной секции занимались 13 студентов, среди которых 5 студентов занимались одновременно в двух секциях. Сколько студентов занималось в хоккейной секции? | |
| Преподаватель решил узнать, кто из 40 студентов курса читал книги А, В и Результаты опроса оказались таковы: книгу А читали 25 студентов, книгу В – 22, книгу С – также 22. Книгу А или В читали 33 студента, А или С – 32, В или С – 31; все три книги прочли 10 студентов. Сколько студентов прочли только по одной книге? Сколько студентов не читали ни одной из этих трех книг? | |
| В группе 25 учащихся. Из них 13 лыжников, 8 пловцов, 17 велосипедистов. Причем каждый спортсмен занимается только двумя видами спорта и учится на «3» или на «4». В группе 6 круглых отличников. Сколько в группе спортсменов? Сколько в группе неуспевающих? |
Задание 4. Найдите элементы множества P, если А = {0,2,3,7,8}; В = {1,3,6,7,9}; С = {0,1,4,7,8,9}; I = {0,1, 2, …,9}.
| Вариант | Задание |
| P=А⋂⌐С⋃А⋂⌐B⋃В⋂C | |
| P=⌐B⋂C⋃⌐А⋂C⋃⌐А⋂B | |
| Р=B⋂⌐С⋃A⋂⌐С⋃A⋂⌐B | |
| Р=⌐B⋂⌐С⋃A⋂C⋃A⋂B | |
| Р=B⋂C⋃⌐А⋂C⋃⌐А⋂B | |
| Р=⌐B⋂C⋃A⋂⌐С⋃A⋂B | |
| Р=B⋂⌐С⋃⌐А⋂⌐С⋃A⋂⌐B | |
| Р=⌐B⋂⌐С⋃A⋂C⋃⌐А⋂⌐B | |
| Р=B⋂C⋃⌐А⋂C⋃A⋂B | |
| Р=⌐B⋂C⋃A⋂⌐С⋃⌐А⋂B |