Расход потока и средняя скорость

 

Одномерными называются течения, в которых основные параметры потока зависят лишь от одной координаты, направление которой совпадает с направлением вектора скорости. Использование одномерных течений позволяет достаточно просто решать многие важные прикладные задачи. Раздел механики жидкости, изучающий одномерные течения, называют гидравликой.

Для решения широкого круга прикладных инженерных задач плодотворной явилась введенная Эйлером так называемая струйная модель потока. Согласно этой модели поток представляется состоящим из бесконечного множества струек жидкости. При рассмотрении потока поперечные сечения в нем выбираются так, чтобы пересекающие их линии тока были нормальны к ним. В этом случае сечение потока называется «живым». Очевидно, что если линии тока параллельны, то живое сечение будет плоским.

Ранее было показано, что элемен­тарный объемный расход несжимаемой жидкости может быть определен как

(3.12)

где u -скорость в сечении струйки, dA - площадь ее поперечного сечения.

В соответствии со струйной моделью расход потока

(3.13)

 

Рисунок 43 – Движение в трубе

 

Рассмотрим движение жидкости в трубе круглого поперечного сечения. В силу тормозящего действия сил вязкого трения распределение скоростей в поперечном сечении трубопровода (эпюра скорости) будет иметь вид, показанный на рисунке 43. Для удобства перейдем к цилиндрическим координатам (r, ), где - полярный угол.

В этой системе

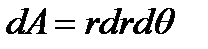(3.14)

Подставляя (3.14) в (3.13) получаем

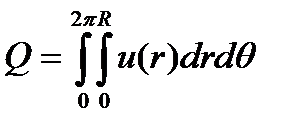(3.15)

Имея в виду, что , имеем

(3.16)

Запись 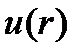обозначает, что местные скорости в сечении трубы изменяются по радиусу. Другими словами, 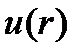описывает закон изменения скорости, т.е. является математическим описанием эпюры. Следовательно, для того, чтобы вычислить расход по (3.16), необходимо знать уравнение эпюры скорости, которое, как правило, неизвестно. Поскольку расход является важнейшим параметром, знание которого требуется при проведении любых гидравлических расчетов, необходимо найти путь, позволяющий преодолеть возникшее затруднение.

Рассмотрим, как решается эта задача в механике жидкости. С чисто математических позиций интеграл в правой части выражает объем эпюры скорости. Представим теперь, что при неизменном расходе Q в силу каких-то причин жидкость потеряла вязкость. Это, очевидно, приведет к тому, что эпюра начнет перестраиваться и, так как исчезнут силы вязкого трения, то все частицы жидкости будут двигаться с какой-то одинаковой скоростью v (рисунок 43), а так как по условию расход остается тем же, то объем новой эпюры равен объему старой. При этом условии , и из (3.16) получаем

(3.17)

Скорость , введенная таким образом носит название средней либо среднерасходной скорости. Следовательно, формально средняя скорость может быть определена как фиктивная скорость, с которой должны были бы двигаться все частицы жидкости для того, чтобы расход был равен его истинному значению.

С физической точки зрения использование понятия средней скорости, одинаковой для всех частиц жидкости в сечении, позволяет свести задачу о движении жидкости в трубах и каналах к одномерной.

Рассмотрим движение в трубе с несколько иных позиций. Если считать его установившимся, то все производные по времени, входящие в уравнение движения, равны нулю. Если исходить из одномерной модели, то равны нулю и компоненты скорости и . При этом из уравнения неразрывности следует, что 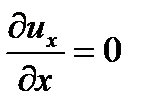Применительно к этому случаю система дифференциальных уравнений Навье-Стокса принимает вид:

(3.18)

 

Последние два уравнения (3.18) совпадают с уравнениями гидростатики, а это означает, что в плоскости поперечного сечения движущейся жидкости давления распределены по гидростатическому закону

(либо (3.19)

Этот вывод приближенно справедлив для слабодеформированных потоков. Под слабодеформированными понимают потоки, у которых угол расхождения линий тока мал, а радиус кривизны - велик, т.е. понятие это носит скорее качественный, чем количественный характер.

Как уже отмечалось, уравнение Навье-Стокса в подавляющем большинстве случаев не поддаются интегрированию. Вместе с тем, практическая деятельность, связанная с необходимостью использования законов движения жидких сред, настоятельно требовала разработки инженерных методов расчета.

Одним из путей решения этой задачи, оказавшимся наиболее плодотворным, явился путь обобщения уравнения Бернулли, т.е. распространения его на поток вязкой жидкости. В основу этого метода, как уже отмечалось, положена струйная модель - представление о потоке как о бесконечно большой сумме струек, протекающих через сечение.

Исходим из того, что движение установившееся и в рассматриваемом сечении поток слабо деформирован. Определим энергию, проносимую секундной массой струйки через сечение (т.е. мощность струйки). Эта величина может быть найдена как произведение полной удельной энергии струйки на ее массовый расход . В справедливости этого легко убедиться непосредственно. Действительно, удельная энергия - Дж/кг, массовый расход - кг/с, их произведение

(3.20)

Секундная энергия (мощность) потока в соответствии со струйной моделью

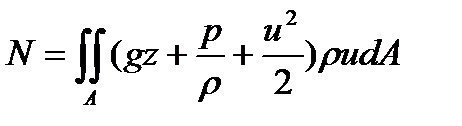(3.21)

либо

(3.22)

Так как поток слабодеформированный, то и первый интеграл принимает вид

(3.23)

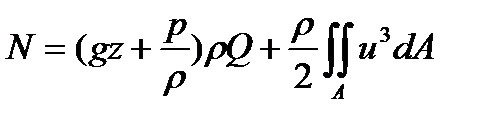(3.24)

По физическому смыслу второй член в (3.24) представляет собой кинетическую энергию секундной массы.

Поскольку мы ограничимся одномерным представлением, то в (3.24) необходимо ввести среднюю скорость. Поступим следующим образом: разделим обе части уравнения на массовый расход Q, т.е. отнесем это соотношение, как и уравнение Бернулли для струйки, к единице массы ( Дж/с; кг/с; 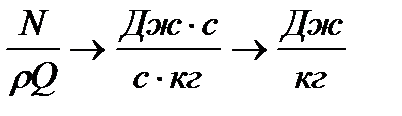и, следовательно, -удельная энергия.

Таким образом, имеем

(3.25)

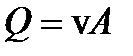Разделив и умножив третий член на квадрат средней скорости , с учетом того, что , получим

(3.26)

Обозначим выражение 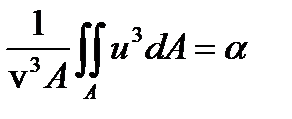; тогда

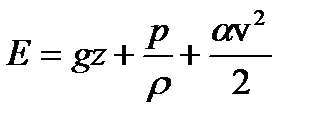(3.27)

Величина носит название коэффициента кинетической энергии, корректива скорости либо коэффициента Кориолиса. Физический смысл этой величины будет раскрыт позже.

Разделив обе части (3.27) на ускорение свободного падения g, выразим это соотношение в единицах длины, т.е. в форме напоров

(3.28)

Рассмотрим движение потока вязкой жидкости в канале (рисунке 44) от сечения 1-1 к сечению 2-2. Обозначим удельную энергию потока в сечении 1-1 через , а в 2-2 - .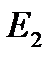

 

Рисунок 44 – Движение вязкой жидкости в канале

 

Так как жидкость вязкая, то процесс ее перемещения сопровождается диссипацией энер­гии, т.е. какая-то ее часть расходуется на преодоление сил внутреннего трения и превращается в тепло, следовательно, . Поэтому баланс энергии для выбранных сечений должен быть записан в виде

(3.29)

где - потери энергии.

Раскрывая значения и 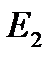, получаем:

(3.30)

Это и есть энергетическая форма уравнения Бернулли для потока вязкой жидкости.

В практических приложениях чаще используют уравнение Бернулли, выраженное в напорах

(3.31)

где - потери напора.

Для газовых потоков (без учета сжимаемости), а также при расчетах систем гидравлического привода обычно используют уравнение Бернулли в форме давлений

(3.32)

где - потери давления.

Обычно в упомянутых системах член оказывается пре­небрежимо малым по сравнению с остальными. В этих случаях (3.32) принимает вид:

(3.33)

Как уже упоминалось, коэффициент носит название коэффициента кинетической энергии, корректива скорости, коэффициента Кориолиса. Выясним физический смысл этой величины.

Как уже отмечалось выше, второй член в уравнении (3.33) представляет собой кинетическую энергию секундной массы потока, определяемую истинным распределением скоростей в сечении, т.е.

(3.34)

Если бы скорости в сечении были бы распределены равномерно, то ( 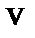- средняя скорость потока), и кинетическая энергия потока была бы

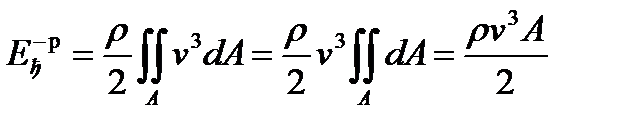(3.35)

Разделив (3.34) на (3.35), получим:

(3.36)

Следовательно, коэффициент Кориолиса представляет собой отношение кинетической энергии потока, вычисленной по истинному распределению скоростей, к кинетической энергии, определенной по средней скорости.

Для уяснения вопроса рассмотрим гипотетический «поток», состоящий из двух струек, скорости которых м/с и м/си вычислим коэффициент Кориолиса.

Истинная кинетическая энергия (сумма кинетических энергий струек)

Подведем некоторые итоги. Использование струйной модели потока и сведение его к одномерному путем введения представления о средней скорости позволяют получить одно из основных уравнений гидродинамики - уравнение Бернулли для потока вязкой жидкости. Принципиально, с помощью этого уравнения можно рассчитать движение жидкости в каналах при установившемся течении и условии, что в выбранных сечениях поток слабодеформированный либо параллельно-струйный. Однако, для полного решения задачи необходимо уметь определять потери напора (), возникающие при движении жидкости в каналах. Эта далеко не простая задача и будет являться предметом дальнейшего рассмотрения.

Если понимать под устойчивостью способность потока подавлять возникающие в нем малые возмущения, то переход к турбулентному режиму может рассматриваться как потеря устойчивости. При этом из двух категорий сил, действующих на жидкие частицы, вязкого трения и инерции, первые играют стабилизирующую роль, а вторые - дестабилизирующую. Таким образом, отношение этих сил может служить критерием (мерой) устойчивости потока, т.е.

В дальнейшем это соотношение получило название числа Рейнольдса, т.е.

(3.37)

где u - характерная скорость течения; l - характерный линейный размер.

Для круглых труб характерный размер - диаметр, характерной скоростью является средняя скорость. С учетом этого, имея в виду, что , выражение (3.37) принимает вид

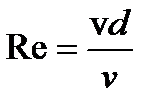(3.38)

При течении в каналах некруглого сечения в качестве характерного размера принимают так называемый гидравлический радиус

(3.39)

где A - площадь поперечного сечения канала; - смоченный периметр (часть периметра, находящаяся в контакте с жидкостью).

Для круглых труб при напорном движени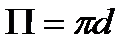и , и 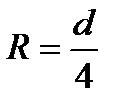, т.е. гидравлический радиус в два раза меньше геометрического.

Одним из наиболее существенных результатов, обнаружен­ных в опытах Рейнольдса являлось то, что переход от ламинарного течения к турбулентному происходил при одном и том же численном значении введенного им критерия устойчивости, названного впоследствии критическим значением числа Рейнольдса (). По данным многочисленных опытов в круглых трубах Это так называемое нижнее критическое число Рейнольдса, которое получают, если не принимать специальных мер по стабилизации потока. При принятии мер, переход к турбулентному течению можно существенно затянуть. При выполнении технических расчетов принято считать, что если число Рейнольдса, вычисленное по фактическим значениям параметров, меньше критического, то режим ламинарный, и наоборот.