Кассациер К.Е.
1. Жизнь на Земле существует в виде экосистем. Экосистема представляет собой единый природный комплекс, образованный живыми организмами и средой их обитания, в котором живые и косные компоненты связаны между собой обменом веществ и энергией. Любая экосистема состоит из биотической и абиотической частей. Биотическая часть – биоценоз - совокупность живых организмов 
биосистемы. Абиотическая часть – биотоп – климатические факторы, а также неорганические составляющие воздуха, воды, почвы и т.п.. Биотическая часть экосистемы построена из богатых энергией органических веществ, абиотическая часть из неорганических, бедных энергией веществ. Характерной особенностью любой экосистемы является непрерывный процесс формирования органических веществ из неорганических (рис.1). Для осуществления этого процесса очевидно необходим внешний источник энергии. В подавляющем числе случаев этой энергией является солнечная энергия. Одновременно с процессом синтеза в экосистеме непрерывно идет процесс разложения органических веществ на неорганические. При этом происходит выделение энергии. Энергия может выделяться в различных формах – в виде тепла, движения, звука, света и т. п.. Таким образом, в любой экосистеме происходит непрерывный переход вещества из абиотической части в биотическую и обратно. Этот круговорот вещества происходит под действием внешней по отношению к экосистеме, как правило, солнечной энергии. В чем причина такого достаточно сложного построения и функционирования экосистемы? Объясняется это фундаментальными законами, управляющими нашей Вселенной, и, в первую очередь, первым и вторым началом термодинамики, определяющими законы преобразования энергии.
2. Все окружающие нас предметы, да и мы сами, состоят из молекул и атомов, находящихся в непрерывном более или менее хаотичном тепловом движении. Известен закон сохранения атомов, который гласит, что при любых химических превращениях атомы не пропадают, не возникают, не изменяются, а лишь переходят из одних соединений в другие. Отсюда следует, что если имеется в какой-либо изолированной системе достаточный по номенклатуре и количеству набор атомов, то, в принципе, из этих атомов можно собрать сложную органическую молекулу, затем можно её разобрать и из тех же атомов заново сложить такую же, либо другую органическую молекулу. Этот процесс можно повторять бесчисленное число раз, как в детском конструкторе – собрал – разобрал и т.д.. Однако в отличие от конструктора атомы в процессе сборки-разборки не портятся, не изменяются и при любом количестве сборок-разборок они ничем не отличаются от первоначального состояния.
При сборке органической молекулы нужно затратить определённую энергию. Эта энергия переходит в энергию химических связей между атомами в органической молекуле. Условно это можно себе представить так, как будто в органической молекуле между атомами находятся пружинки в сжатом состоянии, эти пружинки необходимо сжать при сборке молекулы. Рассмотрим законы управления энергией в окружающем нас мире. Таких основных закона два - первое и второе начало термодинамики.
Первое начало термодинамики – закон сохранения энергии - гласит, что энергия не уничтожается и не появляется, а только переходит из одних форм в другие. При этом нужно учитывать энергию движения молекул и атомов, составляющих тела, входящие в рассматриваемую систему. Эту энергию принято называть внутренней или тепловой энергией. Изменить внутреннюю энергию можно совершив над телом работу (например, сжав газ) или передав этому телу тепло. Обычно понимание первого начала термодинамики не вызывает затруднений.
3. Второе начало термодинамики связано с именем французского инженера Саади Карно, который в начале XIX века дал первую формулировку этого закона. Интересно, что он сформулировал этот закон раньше, чем был сформулирован первый закон термодинамики. На протяжении всего XIX века лучшие умы человечества рассматривали этот фундаментальный закон природы и дали большое число эквивалентных формулировок этого закона. Эквивалентными формулировками закона называются такие формулировки, что приняв в качестве аксиомы одну из них, другие можно вывести из этой аксиомы путем логических заключений. Аксиоматическая формулировка рассматривается просто как результат обобщения экспериментальных фактов.
Начнем с формулировки Карно. Суть закона можно пояснить на следующем примере. Возьмем два деревянных бруска и начнем их тереть друг о друга. При этом бруски начнут нагреваться. Так наши предки добывали огонь. В этом эксперименте происходит преобразование механической энергии в тепловую. Это преобразование происходит без всяких ограничений. Чем больше мы затрачиваем механической энергии, тем больше получаем тепла. Попробуем теперь построить устройство, которое обращало бы рассмотренное действие – проводило перевод тепловой энергии в механическую. То-есть, обеспечивало бы движение брусков друг относительно друга за счет их остывания. Подчеркнем, что создание такого устройства не противоречит первому началу термодинамики. Однако С. Карно утверждает, что создание такого устройства невозможно в соответствии со 2-м началом термодинамики, которое в соответствии с идеями С. Карно можно сформулировать следующим образом.
Нельзя осуществить процесс, единственным результатом которого является превращение тепла в работу при постоянной температуре /1/.
Таким образом, оказывается, что разные виды энергии не равноценны. Так механическая энергия может переходить в тепловую без всяких ограничений, а обратный переход затруднён. В соответствии со 2-м началом термодинамики при каждом преобразовании энергии обязательно часть энергии переходит в тепловую энергию и обратно, в полном объеме, извлечена быть не может. Это приводит к тому, что в изолированной системе с течением времени общее количество энергии в соответствии с 1-м началом не изменяется, однако всё большее и большая её часть оказывается в виде тепловой энергии.
Вернемся к сборке-разборке нашей органической молекулы. При первой сборке нужно затратить определенное количество энергии, которая переходит в энергию химических связей между атомами органической молекулы. При разборке молекулы эта энергия может быть извлечена и сохранена в каких либо аккумуляторах. Однако, как бы мы не совершенствовали процессы разборки и аккумулирования энергии, в соответствии со 2-м началом термодинамики часть энергии обязательно перейдет в тепловую и не сможет быть использована при вторичной сборе молекулы. Таким образом, для поддержания процесса сборки-разборки молекулы нам необходимо использовать внешний источник энергии, который компенсировал бы неизбежное увеличение тепловой энергии. В связи с этим при описании функционирования экосистемы можно говорить о круговороте вещества, но некорректно говорить о круговороте энергии. Для функционирования экосистемы необходим внешний источник энергии.
С. Карно исследовал работу тепловых машин, поэтому его интересовала, в первую очередь, возможность преобразования тепла в механическую работу. В экологии нас интересует возможность использования тепловой энергии для синтеза органических молекул, то-есть возможность превращения тепла в энергию химических связей атомов в молекуле. Можно показать, что энергия химических связей атомов в молекуле также, как и другие виды нетепловой энергии, может быть преобразована в работу при постоянной температуре. Следовательно, постулат Карно можно переформулировать в следующем виде: нельзя осуществить процесс, единственным результатом которого является превращение тепла в другие нетепловые формы энергии при постоянной температуре.
Иногда на вопрос, за счет какой энергии растут грибы, можно услышать ответ. Грибы растут за счет тепла, то-есть тепловой энергии окружающей среды. Но это противоречит постулату Карно. Грибы имеют температуру окружающей среды и, следовательно, не могут использовать тепло для формирования органических молекул. Теплокровные организмы также большую часть времени находятся в состоянии близком к температурному равновесию с окружающей средой. Таким образом, из 2-го начала термодинамики следует важный для экологии вывод. Живые организмы не могут использовать тепло окружающей среды для синтеза органических молекул, для этого они обязательно должны иметь другие источники энергии.
4. Чем определяются особые свойства тепловой формы энергии? На это дают ответ другие эквивалентные формулировки 2-го начала термодинамики. Для того, чтобы разобраться в этом вопросе обратим внимание на следующее обстоятельство. В окружающем нас мире мы наблюдаем процессы двух типов. Первые протекают самопроизвольно, без всякого постороннего воздействия, для протекания других требуется затратить определенные усилия. Например, при контакте горячего и холодного тела всегда тепло потечет от горячего тела к холодному, но никогда наоборот. Горячее тело всегда будет остывать, а холодное нагреваться. Для организации обратного процесса отбора тепла от холодного тела и передачу его горячему (построение холодильника) требуется затратить определенные усилия. При контакте двух растворов разной концентрации всегда самопроизвольно будет протекать процесс выравнивания концентраций, при контакте двух разных газов они будут смешиваться, но никогда разделяться. Вообще в окружающем нас мире всегда существенно проще, что либо смешать, чем разделить, проще сломать, чем построить. И это относится не только к микромиру. Например, нет ничего проще, чем смешать сахарный песок с манной крупой, а попробуйте их разделить. Или другой пример. Пусть у вас имеется приличная по размерам библиотека и вы аккуратный человек. У вас книги расставлены на полках в полном алфавитном порядке. У вас есть младший братик - озорник, который азбуки ещё не знает, но любит книги листать и рассматривать картинки. В ваше отсутствие он сбросил книги с полок и стал их перебирать, рассматривать картинки и т.д.. А потом перед вашим приходом решил их поставить на полку, чтобы ему не попало. Встанут они у него в алфавитном порядке, очевидно, что практически никогда.
Как объяснить все эти факты. Можно рассматривать их как экспериментально полученные факты, которые обосновывают следующую эквивалентную формулировку 2-го начала – тепло не может перетечь само собой от холодного тела к горячему /1/.
Для понимания дальнейшего необходимо знакомство читателя с теорией вероятности. К сожалению, при изучении экологии студенты, как правило, еще не знакомы с этой теорией. Постараемся дальнейший материал изложить, основываясь на интуитивном представлении о равновероятных событиях.
Основной объект изучения теории вероятности – процедура подбрасывания монеты. Основная особенность этого эксперимента заключается в том, что до начала опыта невозможно предсказать, что выпадет в результате – орел или решка. Говорят, что эти события равновероятны. Однако, удивительно, но факт, если провести серию из n таких бросаний, результат каждого из которых невозможно предсказать, и подсчитать число выпадения «орлов» в серии, то результат становится предсказуемым, причем с тем большей достоверностью, чем больше длина серии n. Именно поэтому теория вероятности является теорией. Почему так происходит? Постараемся это понять на простом примере.
Рассмотрим возможные результаты серии из n бросаний. Пусть, например, n= 4. Будем для простаты обозначать выпадение «орла» через 1, а «решки» - через 0. Могут в результате бросаний выпасть все 4 нуля, конечно, могут. Может, например, сначала выпасть 1, а потом три нуля? Конечно, может. А сколько всего может быть различных результатов N из n бросаний? Не трудно догадаться, что их будет N =2 n .
На рис. 2 приведены все возможные исходы результатов серий из 4-х бросаний. Принципиальным является то, что каждый из этих 16 результатов не имеет ни каких преимуществ перед другими. Все 16 возможных результатов являются равновероятными событиями. Однако, мы видим, что случай, когда единица отсутствует, встречается один раз из 16, а случай, когда выпадает две единицы в серии встречается 6 раз. Если теперь нас попросят предсказать, что получится в результате проведения серии из четырех бросаний, мы, очевидно, скажем, что скорей всего выпадет 2 единицы. А что будет при увеличении n? При увеличении n общее число возможных результатов N= 2 n быстро растет, например, при n= 10 N= 1024, из которых только в одном случае не выпадет ни одной единицы, а в 252 случаях число единиц будет равно r=n/2= 5.
 Можно сообразить, что число различных реализаций в серии из n бросаний монеты, содержащих ровно r единиц, равно числу сочетаний из n по r, Cnr . Числа Cnr являются коэффициентами бинома Ньютона. Из школьного курса известно выражение
Можно сообразить, что число различных реализаций в серии из n бросаний монеты, содержащих ровно r единиц, равно числу сочетаний из n по r, Cnr . Числа Cnr являются коэффициентами бинома Ньютона. Из школьного курса известно выражение
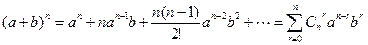 (1)
(1)
 (2)
(2)
Если положить a=b= 1, то получим представление общего числа возможных исходов в серии из n бросаний монеты в виде суммы, каждое слагаемое которой показывает, сколько среди этих исходов будет исходов с числом единиц равным r.
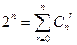 (3)
(3)
Анализ численных значений биномиальных коэффициентов показывает, что с увеличением числа бросаний n резко увеличиваются число исходов с числом единиц в серии близким к n/2.
Философы широко обсуждают вопросы: каким образом в нашем мире случайность соотносится с детерминизмом, каким образом закономерность пробивает дорогу через случайность? Анализ поведения биномиальных коэффициентов освещает этот вопрос. Поистине, как сказал один известный физик, в биноме Ньютона заключена вся суть мироздания.
5. Перейдем теперь от математики к физике. Рассмотрим замкнутый сосуд, содержащий n молекул газа. Разделим мысленно сосуд на две половинки, и определим, сколько молекул будет находиться в левой половине сосуда в некоторый фиксированный момент времени. Так как молекулы находятся в непрерывном хаотическом тепловом движении, то любая молекула независимо от положения других молекул в каждый фиксированный момент времени с одинаковой вероятностью может оказаться в любой половине сосуда. То-есть, попадание молекулы в левую половину аналогично получению единицы при подбрасывании монеты, а попадание в левую половины r молекул эквивалентно выпадению r единиц в серии из n бросаний. Конечно, распределение молекул между половинами сосуда будет непрерывно меняться. В принципе все молекулы могут случайно собраться в левой половине или наоборот в правой или распределяться между половинками более или менее равным образом. Аналогия с серией подбрасывания монеты позволяет понять, что, если, например, в сосуде содержится 4 молекулы то примерно 1\16 часть времени наблюдения они будут находиться все в левой половине, 1\16 в правой, 6\16 времени наблюдения они будут поровну распределены между половинками сосуда.

При n =10 молекулы будут находиться все в левой половине в среднем в течении 1\1024 времени наблюдения, при n =1000 в течении только 10-301 части времени наблюдения. Реально обычно мы имеем дело с существенно большими значениями n. Так, например, в 1 см3 кислорода при температуре 0оС и атмосферном давлении содержится 1019 молекул.
На рис.3 приведены результаты 3-х экспериментов по 100 серий подбрасывания монет в каждом. (Подбрасывание монеты моделировалось с помощью компьютерной программы). Эксперименты отличались числом n (число подбрасываний монеты в серии или число молекул газа в сосуде). На графике рис. 3 по оси ординат отложено значение r/n, где r число молекул в левой половине сосуда. На рисунке синяя кривая соответствует n= 4, зелёная n= 10, красная n= 1000. Из приведенных данных видно, что число молекул в левой половине сосуда, также как и в правой, будет с течением времени флюктуировать относительно величины n/ 2. Причем относительная величина этих флюктуаций будет быстро уменьшаться с увеличением числа молекул. Если в начальный момент все молекулы были собраны в одной половине, то из этого состояния они самопроизвольно перейдут в состояние примерного равного числа молекул в обеих половинках сосуда и будут в дальнейшем флуктуировать относительно этого положения. Принято говорить, что в этом состоянии обе половинки сосуда находятся в состоянии термодинамического равновесии друг с другом. Состояние, когда молекулы сгруппированы в одной половине сосуда, является маловероятным состоянием, в то время как при больших n состояние с близким к равномерному распределению молекул имеет существенно большую вероятность. Система, предоставленная сама себе, переходит самопроизвольно из состояния имеющего меньшую вероятность в состояние большей вероятности. Или другими словами самопроизвольно система стремиться к состоянию термодинамического равновесия.
Рассмотрим другой пример. Пусть в начальном состоянии сосуд разделен перегородкой на две половины, по разные стороны от которой находятся молекулы разных газов. После удаления перегородки каждая молекула, независимо от вида газа, вследствие теплового движения с одинаковой вероятностью может находиться в любой половине сосуда. Следовательно, в соответствии с вышеизложенным, молекулы как одного, так и другого газа распределяться приблизительно равномерно по обеим половинам, то-есть газы самопроизвольно перемешаются. Аналогичная ситуация будет иметь место и при соприкосновении растворов разной концентрации, они самопроизвольно могут только выравниваться. При соприкосновении горячих и холодных масс по аналогичной причине за счет перемешивания «горячих» и «холодных» молекул будет происходить выравнивание температур. Во всех случаях системы будут самопроизвольно переходить из состояний, имеющих малую вероятность, в состояние с наибольшей вероятностью, или, другими словами, самопроизвольно будут стремиться к состоянию термодинамического равновесия.
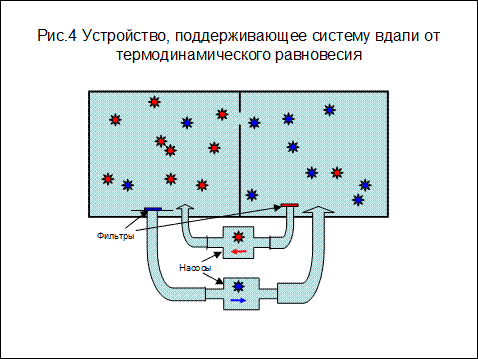
Рассмотрим опять ситуацию с двумя разными газами, отделёнными друг от друга перегородкой. Пусть, например, слева будут молекулы обозначаемые красным цветом, а справа синим (рис. 4). Пусть на перегородке появилось небольшое отверстие, через которое могут перемещаться молекулы между половинами сосуда. Для того, чтобы молекула перешла из одной половины сосуда в другую необходимо, чтобы в процессе теплового движения молекула оказалась перед отверстием и, чтобы её скорость оказалась направленной в сторону отверстия. Очевидно, чем больше молекул данного класса находится в рассматриваемой половине сосуда, тем чаще будет выполняться это условие, и молекулы данного класса самопроизвольно потекут из той половины, где их больше, в ту половину, где их меньше. Процесс будет протекать до тех пор, пока концентрации газов в половинках сосуда не выровняются, то-есть система не прейдет в состояние термодинамического равновесия.
А теперь предположим, что нам нужно поддержать первоначальный порядок или рассортировать по половинкам сосуда газы, если они оказались перемешены. Другими словами необходимо либо удерживать систему в состоянии, удаленном от термодинамического равновесия, или вывести её из состояния термодинамического равновесия. Для этого необходимо задействовать некое устройство, которое бы перекачивало «красные» молекулы из правой половины в левую, а «синие» наоборот. Очевидно, для этого необходимо затрачивать какую то энергию. Но одной энергии мало. Для того, чтобы поддерживать систему в удаленном от термодинамического равновесия состоянии необходимо иметь определенную информацию о порядке, который мы собираемся поддерживать в системе. Мы должны заранее знать, в какой половине сосуда необходимо концентрировать «красные» молекулы, а в какой «синие». Необходимо знать, по каким свойствам «красные» молекулы отличаются от «синих», чтобы построить устройство, обеспечивающее перекачку в одну сторону только
 |
«красных», а в другую только «синих» молекул. Таким образом, мы видим, что если в направлении установления термодинамического равновесия процесс идет самопроизвольно без всяких внешних усилий, то обратный процесс или просто поддержка неравновесного состояния требует определенных энергетических затрат и применения достаточно сложных устройств, использующих информацию о характере неравновесного состояния.
6. В предыдущем примере, когда газы разделены в сосуде, мы воспринимаем это состояние, как состояние определенного порядка в системе. Напротив, когда газы перемешаны, это воспринимается как отсутствие порядка или беспорядок, хаос. Из этого примера можно предположить, что понятие порядка связано со степенью удаления системы от положения термодинамического равновесия или, другими словами, порядок характеризуется менее вероятным состоянием системы по сравнению с беспорядком.
Вернёмся к примеру расстановки книг в библиотеке. При наличии n книг их можно расставить на полке N=n! способами. Из этих способов только один способ установки соответствует полному алфавитному порядку, а остальные n!- 1соответствуют беспорядочной установке. Порядка может быть больше или меньше. Например, можно устанавливать книги в алфавитном порядке по фамилиям авторов, но при наличии однофамильцев, не обращать внимание на имена, а устанавливать книги однофамильцев в произвольном порядке. Очевидно, что при такой расстановке порядка будет меньше и ему будет соответствовать не одно, а большее число различных размещений. Понятия порядка и беспорядка являются дополняющими друг друга понятиями. При увеличении порядка в системе уменьшается количество беспорядка и наоборот. Принято степень беспорядка в системе количественно оценивать логарифмом от числа возможных равновероятных состояний системы, которые соответствуют понятию беспорядка.
S=log N (4)
S - носит название энтропии системы.
Чем больше элементов входит в систему, тем больше возможная в ней степень беспорядка, больше энтропия системы. Например, при произвольном распределении атомов между половинками сосуда энтропия системы будет пропорциональна числу атомов
S=logN=log 2n =n log2 (5)
В случае, если система упорядочена таким образом, что установленному порядку соответствует единственное состояние элементов системы (например, книги установлены в строгом алфавитном порядке), то энтропия в этом случае будет равна нулю
S=log 1 =0, (6)
что соответствует полному порядку, установленному в системе.
Таким образом, порядка в системе тем больше, чем меньшее число возможных равновероятных состояний системы удовлетворяет этому порядку. Чем больше порядка в системе, тем дальше она находится от состояния термодинамического равновесия. В соответствии с вышеизложенным, система самопроизвольно стремиться перейти из менее вероятного состояние в более вероятное, то-есть из состояния большего порядка к состоянию меньшего порядка. Это отражается в ещё одной эквивалентной формулировке 2-го начала термодинамики – энтропия в изолированной системе не может уменьшаться с течением времени.
Подчеркнем, что этот закон относится ко всей системе в целом. Следовательно, он не исключает возможность уменьшения энтропии, увеличения порядка в некоторой части изолированной системы, однако при этом будет увеличиваться энтропия, уменьшаться порядок, в окружающих эту подсистему частях общей системы. Иногда говорят, что для того чтобы установить или поддерживать порядок в некоторой системе необходимо из неё непрерывно откачивать самопроизвольно возрастающую энтропию.
Отметим, что в курсе физики при изложении 2-го начала термодинамики вводится понятие энтропии как функции состояние системы, изменение которой равно количеству подводимого к системе тепла, деленному на абсолютную температуру. Можно показать, что это определение эквивалентно рассмотренному выше, так называемому статистическому определению энтропии. Отличие заключается только в используемых единицах измерения энтропии.
С понятием порядка и беспорядка связано понятие информации и правило её количественного определения. Говоря о порядке, следует указать, что в отличие от беспорядка, в системе может быть установлено много различных порядков. Например, можно установить в книги в алфавитном порядке от А до Я, а можно установить в обратном порядке от Я до А. Можно установить по возрастанию числа страниц в книгах, а можно упорядочить по цвету корешков и т. п.. Для того чтобы установить и поддерживать определенный порядок в системе необходимо иметь информацию об этом порядке. Количество информации измеряется по величине уменьшения энтропии системы при её переводе из начального состояния в состояние, определяемое заданной информацией.
7. Из вышеизложенного следует, что «порядок менее вероятен, чем беспорядок, и если легко получить беспорядок, исходя из порядка, то вообще нужно немало усилий, чтобы из беспорядка создать порядок» /2/. Рассмотрим некую систему, которая характеризуется определенным, установленным в ней порядком. В соответствии с вышеизложенным, это значит, что составляющие систему элементы находятся в определенном взаимоотношении между собой. При этом число возможных взаимоотношений между элементами, составляющими систему, при котором система сохраняет свою идентичность, свой порядок, существенно меньше общего числа возможных взаимоотношений между этими элементами. Поэтому тепловое хаотическое движение, которое всегда имеет место, будет всегда стремиться перевести взаимодействующие элементы системы в более вероятное состояние, то-есть разрушить систему.
Таким образом, из второго начала термодинамики следует, что любой порядок самопроизвольно разрушается, любая структура, предоставленная самой себе, обязательно разрушается. Этот закон является фундаментальным законом природы, применимым как к живой, так и к неживой природе. Рассмотрим, например, автомобиль. Работоспособный автомобиль представляет собой определенную систему, в которой атомы, входящие в его состав и составляющие его шестеренки, контакты и т.п., расположены в определенном порядке друг относительно друга. Среди всевозможных их взаимных расположений в пространстве, занимаемом автомобилем, число расположений, при которых автомобиль остается работоспособным существенно меньше числа расположений, при которых он неисправен. Поэтому, в соответствии со 2-м началом, при эксплуатации автомобиль будет неизбежно ломаться. Для поддержания автомобиля в рабочем состоянии необходимо его систематически ремонтировать, то-есть менять изношенные детали, восстанавливать контакты и т.д.. А для этого принципиально необходимы три вещи. Во-первых, материя, вещество, из которых можно изготавливать необходимые детали взамен вышедших из строя, во-вторых, необходима энергия для изготовления и установки этих деталей, и, в-третьих, необходима информация, чертежи, используемые при изготовлении и установке деталей. Живые организмы отличаются от неживых систем тем, что они несравненно более сложны, в них гораздо больше порядка, они находятся существенно дальше от состояния термодинамического равновесия с окружающей их средой, чем любые системы неживой природы, естественные или созданные человеком. В связи с этим разрушающее действие 2-го начала на них проявляется значительно сильней, чем на объекты неживой природы. Противостоят этому разрушительному воздействию живые организмы тем, что они выработали у себя способность к непрерывному самостоятельному «ремонту». В любой живом организме производится непрерывная замена отработанных частей (молекул, клеток и т.п.) на новые. При прекращении «ремонта» организм погибает. А для проведения такого «ремонта», как мы видели, принципиально необходимо три вещи – вещество, энергия и информация. Информацию организм получает от родителей в виде молекул ДНК, а вещество и энергию из окружающей среды. Таким образом, в соответствии со 2-м началом термодинамики любой живой организм с необходимостью является открытой системой производящей обмен веществ с окружающей средой и получающей из этой среды энергию.
При обмене веществ с окружающей средой в любом живом организме непрерывно проходят процессы синтеза и разложения органического вещества, процессы анаболизма и катаболизма.
Анаболизмом или ассимиляцией называется совокупность химических процессов в живом организме, направленных на образование и обновление структурных частей клеток и тканей, на синтез сложных молекул из более простых. Процессы анаболизма идут с поглощением энергии и с накоплением энергии в виде химических связей сложных соединений.
Катаболизмом или диссимиляцией называется совокупность протекающих в живом организме химических процессов расщепления органических веществ на более простые. Эти процессы идут с выделением энергии.
Совокупность процессов анаболизма и катаболизма называют метаболизмом. В соответствии со 2-м началом при проведении процессов синтеза и разложения, связанных с преобразованием энергии, часть энергии обязательно переходит в тепловую энергии, следовательно, для поддержания метаболизма необходимо получение живым организмом энергии из окружающей среды. Интенсивность метаболизма определяется количеством энергии в единицу времени, мощностью, необходимой для поддержания метаболизма живого организма, то-есть для поддержания его жизни.
Какую, например, мощность должен получать человек для поддержания своей жизни? Эта цифра хорошо известна – около 3000 ккал в сутки, или, если перевести калории в джоули (1 кал=4.2 Дж), а сутки в секунды, получим около 150 Вт. Это среднее энергопотребления человека, необходимое для поддержания его жизни. Отметим, что если мы будем бежать вверх по лестнице или колоть дрова и т.п., то в этом случае мы работаем как некоторый механизм, производящий определенную работу за счет преобразования химической энергии, выделяемой при разложении органических молекул, в механическую энергию. При этом естественно наше энергопотребление должно возрастать. Однако важно, что даже в том случае, если мы ляжем на диван, полностью расслабимся и не будем производить никакой внешней работы, то и в этом случае потребуется затраты энергии для поддержания жизни. Действительно, даже в этом случае, непрерывно в клетках будут происходить химические реакции под управлением белковых молекул, эти молекулы будут разрушаться, их необходимо заменять на новые, огромное количество клеток будет разрушаться, их необходимо заменять на новые и т.п.. Для поддержания этих процессов необходима непрерывная работа транспортных систем организма (легких, сердечнососудистой системы и др.), обеспечивающих поставку ко всем клеткам организма необходимых для поддержания метаболизма веществ и отвод продуктов распада. Таким образом, даже в случае полного покоя живой организм вынужден тратить энергию для поддержания жизни. Эти затраты носят название основного метаболизма и по величине составляют для человека около 2/3 общего метаболизма.
8. Интенсивность метаболизма является важнейшей характеристикой живого организма. Как связана эта интенсивность со свойствами организма? Очевидно, что тем больше размеры, биомасса организма, тем выше интенсивность метаболизма. Слону нужно значительно больше пищи, чем бабочке. Однако, эта зависимость не прямо пропорциональная. Принято считать, что интенсивность метаболизма A связана с биомассой организма B следующим соотношением /3/:
A=aB3/4 (7)
Эта зависимость приведена на рис. 5 (сплошная синяя кривая).
 Объяснить отклонение от линейной зависимости можно следующим образом. Слон состоит из n живых клеток. Если бы эти клетки разбежались и стали жить самостоятельно, очевидно, что их совокупный метаболизм в n раз превышал бы метаболизм одной клетки. Живя в составе слона, клетки взаимодействуют друг с другом, что облегчает их существование и уменьшает количество необходимой энергии для поддержания жизни. Клетки получают пользу от совместного проживания в теле слона, если бы это было бы не так, многоклеточные организмы не возникли бы в ходе эволюции.
Объяснить отклонение от линейной зависимости можно следующим образом. Слон состоит из n живых клеток. Если бы эти клетки разбежались и стали жить самостоятельно, очевидно, что их совокупный метаболизм в n раз превышал бы метаболизм одной клетки. Живя в составе слона, клетки взаимодействуют друг с другом, что облегчает их существование и уменьшает количество необходимой энергии для поддержания жизни. Клетки получают пользу от совместного проживания в теле слона, если бы это было бы не так, многоклеточные организмы не возникли бы в ходе эволюции.
В экологии часто используют понятие удельного метаболизма Е,
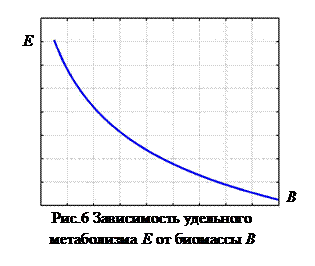 E=A/B=aB-1/4 , (8) определяющего количество энергии, необходимой для поддержания жизни единицы массы данного организма. Зависимость удельного метаболизма от биомассы организма приведена на рис.6. Таким образом, чем мельче организм, тем меньшую биомассу этих организмов может поддержать заданный поток энергии.
E=A/B=aB-1/4 , (8) определяющего количество энергии, необходимой для поддержания жизни единицы массы данного организма. Зависимость удельного метаболизма от биомассы организма приведена на рис.6. Таким образом, чем мельче организм, тем меньшую биомассу этих организмов может поддержать заданный поток энергии.
| Тип организма | Коэффи-циент а |
| Одноклеточные | 0.07 |
| Грибы | 0.09 |
| Высшие растения | 0.1 |
| Черви | 0.12 |
| Насекомые | 0.22 |
| Рыбы | 0.28 |
| Пресмыкающиеся | 0.63 |
| Млекопитающие | 3.5 |
| Птицы | 3.8 |
Интенсивность метаболизма зависит не только от размеров организма. Чем выше организация организма, чем больше в нём упорядоченности, тем дальше он от состояния термодинамического равновесия с окружающей средой и, следовательно, тем больше энергии необходимо затрачивать для поддержания его упорядоченности. Это обстоятельство отражается значением коэффициента а в формулах (7) и (8). Значения коэффициента а для разных типов организмов приведены в таблице (данные взяты из /3/). Обращает на себя внимание резкое увеличение интенсивности метаболизма при переходе от пресмыкающихся к млекопитающим и птицам.
Такой скачек связан с переходом от холоднокровных организмов к теплокровным. Для поддержания постоянной температуры тела необходимы большие затраты энергии. Например, динозавру требовалось для прокорма примерно в шесть раз меньше пищи, чем млекопитающему тех же размеров. Это колоссальное конкурентное преимущество. Поэтому, хотя млекопитающие появились примерно 200 млн. лет тому назад, они долго не могли потеснить динозавров. Только около 60 млн. лет назад, при резком похолодании, способность поддерживать постоянной температуру тела стало решающим преимуществом, и млекопитающие и птицы потеснили пресмыкающихся.
Таким образом, высокая степень порядка и соответственно высокая степень удаленности от состояния термодинамического равновесия с окружающей средой, свойственная любой живой системе (организму или экосистеме), приводит к тому, что для поддержания жизни любой организм должен обмениваться с внешней средой веществом, получать из внешних источников энергию и обладать определенным количеством информации о своей структуре. Из этих трех составляющих энергия и информация являются абсолютно необходимыми для любой живой системы. Экосистема отличается от отдельного живого организма тем, что за счет круговорота элементов внутри экосистемы, она может в принципе обходиться без обмена веществом с окружающей средой.
Литература
1. Р. Фейнман, Р. Лейтон, М.Сэндс. Феймановские лекции по физике. т.4 Из-во «Мир», М., 1967 стр.105.
2. Эмиль Борель. Вероятность и достоверность. Из-во «Наука» М. 1964 стр.56.
3. Т.А. Акимова. Экология. Учебн. для вузов, ЮНИТИ, 1999 г