Первый закон термодинамики
Начнём с обсуждения работы газа.
Газ, находящийся в сосуде под поршнем, действует на поршень с силой 
, где 
— давление газа, 
— площадь поршня. Если при этом поршень перемещается, то газ совершает работу.
При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).
Работа газа в изобарном процессе
Предположим, что газ расширяется при постоянном давлении . Тогда сила 
, с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние 
(рис. 1).
Рис. 1. 
Работа газа равна:
Но 
— изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:
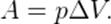(1)
Если 
и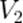 
— начальный и конечный объём газа, то для работы газа имеем: 
. Изобразив данный процесс на 
-диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2).
Рис. 2. Работа газа как площадь
Пусть теперь газ изобарно сжимается от объёма до объёма 
. С помощью аналогичных рассуждений приходим к формуле:
Но 
, и снова получается формула (1).
Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.
Итак, формула 
выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.
Работа газа в произвольном процессе
Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.
Действительно, рассмотрим малое изменение 
объёма газа — настолько малое, что давление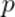 
будет оставаться приблизительно постоянным. Газ совершит малую работу 
. Тогда работа 
газа во всём процессе найдётся суммированием этих малых работ:
|
|
Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3):
Рис. 3. Работа газа как площадь
Работа, совершаемая над газом
Наряду с работой 
, которую совершает газ по передвижению поршня, рассматривают также работу 
, которую поршень совершает над газом.
Если газ действует на поршень с силой 
, то по третьему закону Ньютона поршень действует на газ с силой 
, равной силе по модулю и противоположной по направлению: 
(рис. 4).
Рис. 4. Внешняя сила 
, действующая на газ
Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:
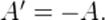
Так, в процессе расширения газ совершает положительную работу 
; при этом работа, совершаемая над газом, отрицательна 
<="" 0="" \right="")'="" class="tex" alt="\left ({A}" style="max-width: 100%; height: auto; vertical-align: middle; border: 0px;">. Наоборот, при сжатии работа газа отрицательна 
, а работа, совершаемая поршнем над газом, положительна 
0 \right)' class='tex' alt='\left ({A}' > 0 \right)' />.
Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа .
Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.
Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты 
, и если в то же время над телом совершена работа , то изменение внутренней энергии тела будет равно:
|
|
(2)
Нас больше всего интересует случай, когда тело является газом. Тогда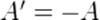 
(где , как всегда, есть работа самого газа). Формула (2) принимает вид: 
, или
(3)
Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.
Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.