И контекстно-свободные языки

Введение

 

Изложенный здесь материал на протяжении ряда лет читался профес­сором Вернером Куихом в курсе «Теоретическая информатика» для сту­дентов Венского технического университета. Данное пособие может рас­сматриваться лишь как краткий конспект лекций, читаемых авторами для студентов математического факультета Калининградского госуниверси­тета, и не является заменой последних.

В пособии изложены основы теории формальных языков и грамматик, включая регулярные, контекстно-свободные грамматики и грамматики Ван Вайнгаардена, а также теория автоматов применительно к анализу фор­мальных языков, включая конечные автоматы, магазинные автоматы и машины Тьюринга. Далее даны основы теории алгоритмов и рекур­сивных функций, где особое внимание уделено вопросам вычислимости. В последней главе рассмотрены проблемы весьма актуальной сейчас тео­рии сложности.

В конце пособия приведены упражнения по изложенным темам вме­сте с их краткими решениями, что необходимо для практического закреп­ления материала.

 

ГРАММАТИКИ, АВТОМАТЫ

И КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ

Алфавит есть непустое конечное множество. Элементы алфавита назы­ваются символами. Пусть S – алфавит. Множество всех слов над S, а именно

S^* = { x ₁ x ₂ …x_n | x_i ÎS, 1£ i £ n, n ³0}

вместе с операцией конкатенации образуют свободный моноид, порожден­ный S, с единичным элементом e (для n = 0). Через | w | обозначим длину слова w ÎS^*: | x ₁… x_n | = n, n ³1, |e| = 0. Очевидно, выполняется | w₁w₂ | = | w ₁| + | w ₂|. Отображение | |: S^* ® ¥, где ¥ – неотрицательные целые числа {0, 1, 2,...} есть гомоморфизм моноида <S^*, ×, e> на моноид <¥, +, 0>.

Каждое подмножество L множества S^*, т.е. L Í S^*, называется формаль­ным языком над S. Пусть L ₁ и L ₂ формальные языки над S, т.е. L ₁, L ₂ Í S^*. То­гда определим произведение L ₁ и L ₂ как L ₁× L ₂= { w ₁ w ₂ | w ₁Î L ₁, w ₂Î L ₂} Í S^*.

Естественно <P(S^*), ×, {e}> снова моноид. (Через P обозначим степень множества.) Он называется моноидом формальных языков.

Для L Í S^* мы можем с помощью произведения определить степени:

L ⁰ = {e}, L^{n +1} = LLⁿ = LⁿL, n ³0.

L ^* определяется как L ^* = ⁿ. Нам потребуется также L ⁺ = ⁿ. Оче­видно, выполняется L ^* = {e} È L ⁺ и L ⁺ = LL ^* = L ^* L.

В случае, если множество М содержит в точности один элемент, М = { а }, то мы также будем писать, если не возникнет путаницы, просто а. Справедливо: aⁿ = a … a (n раз) и a ^* = { aⁿ | n ³0}.

Пусть S – множество. Каждое подмножество R множества S ´ S, т.е. R Í S´S, называется (двухместным) отношением над S. Если (s ₁ ,s ₂)Î R, то мы пишем s ₁ Rs ₂.

Пусть R – отношение над S. Транзитивное замыкание R⁺ определяется следующим образом: t ₁ R⁺t ₂в точности тогда, если существуют s ₁, s ₂, …, s_n Î S, n >1, такие что t ₁ = s ₁, t ₂ = s_n и s_jRs_j+1, 1£ j £ n -1. Рефлексивное и тран­зитивное замыкание R ^*определяется следующим образом: t ₁ R ^* t ₂ в точно­сти тогда, если t ₁ = t ₂ или t ₁ R⁺t ₂.

Грамматики есть математические системы, служащие для порождения формальных языков. Для определения синтаксиса языка программирова­ния они чрезвычайно важны. Множество синтаксически правильных про­грамм (причем содержание программ не принимается во внимание) может пониматься как формальный язык. Этот формальный язык определяется в общем случае через контекстно-свободную грамматику в нормальной форме Бэкуса.

Контекстно-свободная грамматика есть четверка G = (Ф, S, P, S). Причем

(i) Ф – алфавит, называемый алфавитом переменных, или нетерми­нальных символов;

(ii) S – алфавит, называемый алфавитом базовых,или терминаль­ных, символов, где Ф Ç S = Æ, V = Ф È S;

(iii) P Ì Ф´(Ф È S)^* – конечное множество, называемое множест­вом продукций;

(iv) S ÎФ – начальная переменная.

Пусть G = (Ф, S, P, S) – контекстно-свободная грамматика. Тогда Þ _G (или просто Þ) – отношение на V ^*, которое определено следующим обра­зом: j Þ y тогда и только тогда, когда j = g A d, y = gad и (A,a)Î P.

Говорят, что j прямо выводит y, или y может быть непосредственно выведено из j.

Пусть отношение Þ (или просто Þ^*) рефлексивное и транзитивное за­мыкание отношения Þ _G. Говорят, что j выводит y, или y может быть выведено из j.

Пусть G = (Ф, S, Р, S) – контекстно-свободная грамматика. Тогда обо­значим L (G) – язык, порожденный G, причем выполняется:

L (G) = { w | w ÎS^* и S Þ w }.

Если (А,a)Î Р, то пишем также А ® _G a, или А ®aÎ P.

Пример 1.1. Пусть G = ({ S }, {(,)}, P, S) с P = { S ®(S) S, S ®e}. Тогда L (G) – есть множество всех корректных скобочных выражений над скоб­ками (и). Например: (())() Î L (G), так как это выражение может быть вы­ведено из S:

S Þ (S) S Þ ((S) S) S Þ (() S) S Þ (()) S Þ (())(S) S Þ (())() S Þ (())().

Таким образом, выполняется S Þ^* (())(), и тем самым (())() лежит в L (G).

Грамматика G ’ = ({ S }, {(,)}, P ’, S) с P ’ = { S ® SS, S ®(S), S ®e} порож­дает тот же самый язык. Однако правила вывода имеют другую структуру:

S Þ SS Þ (S) S Þ ((S)) S Þ (()) S Þ (())(S) Þ (())().

Тем самым показано, что (())()Î L (G ’). □

 

Если синтаксис языка программирования определяют через контек­стно-свободную грамматику, то продукции часто представляют в нормаль­ной форме Бэкуса. При этом переменные пишутся в форме < w >, где w – непустое слово над алфавитом V_Z. Если < w > ® a₁, …, < w > ® a _n – все про­дукции с левой частью < w >, то пишут

< w >::= a₁|a₂|…|a _n.

Алфавиты Ф, V_{Z ,} S не всегда указаны. Кроме того, разрешена следую­щая конструкция: a_j может иметь вид g₁{g₂}g₃. Это означает, что возможны прямые выводы:

< w > Þ g₁g₂ ⁿ g₃, n ³0.

Пример 1.2. В языке PASCAL константы определяются в разделе опи­сания констант. Синтаксис раздела описания констант задается следую­щими правилами (в нормальной форме Бэкуса):

 

<раздел описания констант>::= <пустой>| const <определение константы> {;<определение константы>};

<определение константы>::=<идентификатор константы> = <константа>

<идентификатор константы>::= <идентификатор>

<идентификатор>::= <буква>{<буква или цифра>}

<буква или цифра>::= <буква>|<цифра>

<буква>::= A|B|C|D|E|F|G|H|I|J|K|L|M|N|O|P|Q|R|S|T|U|V|W|X|Y|Z

<цифра>::= 0|1|2|3|4|5|6|7|8|9

<константа>::= <число без знака>|<знак><число без знака>|

<идентификатор константы>|<знак><идентификаторкон­станты>

<число без знака>::= <целое без знака>|<вещественное без знака>

<целое без знака>::= <цифра>{<цифра>}

<вещественное без знака>::= <целое без знака>.<цифра>{<цифра>}|

<целое без знака>.<цифра>{<цифра>}Е

<характеристика>|<целое без знака>Е

<характеристика>

<характеристика>::= <целое без знака>|<знак><целое без знака>

<знак>::= +|-

<пустой>::= e

Определение константы

const PI = 3.14; E = 2.73;

синтаксически правильно, так как существует вывод:

<раздел описания констант>

Þ const <определение константы>;<определение константы>;

Þ const <идентификатор константы>=<константа>;<определение кон­станты>;

Þ const <идентификатор>=<константа>;<определение константы>;

Þ const <буква><буква или цифра>=<константа>;<определение кон­станты>;

Þ const <буква><буква>=<константа>;<определение константы>;

Þ const Р <буква> = <константа>;<определение константы>;

Þ const РI = <константа>;<определение константы>;

Þ const РI = <число без знака>;<определение константы>;

Þ const РI = <вещественное без знака>;<определение константы>;

Þ const РI = <целое без знака><цифра><цифра>;<определение кон­станты>;

Þ const РI = <цифра><цифра><цифра>;<определение константы>;

Þ^* const РI = 3.14;<определение константы>;

Þ^* const PI = 3.14; E = 2.73; □

Формальный язык L Í S^* называется контекстно-свободным тогда и только тогда, когда имеется контекстно-свободная грамматика G, такая что L (G) = L. Множество всех выражений, правильно заключенных в скобки, и множество всех синтаксически правильных определений констант есть, таким образом, контекстно-свободные языки.

Каждому выводу в контекстно-свободной грамматике G = (Ф, S, Р, S) можно поставить в соответствие направленное дерево, так называемое де­рево вывода, узлы которого обозначаются символами из V:

(1) Выводу S Þ A ₁ A ₂… A_n, A_j Î V, 1£ j £ n, соот­ветствует дерево вывода:

 

 

(2) Пусть выводу S Þ^* a₁ A a₂, a₁,a₂ Î V ^*, A ÎФ, соответствует дерево вывода:

 

 

 

Тогда выводу S Þ^* a₁ A a₂ Þ a₁ A ₁… A_n a₂, A_j Î V соответствует дерево вы­вода:

 

 

Метки конечных узлов, если они при про­хож­дении по дереву вывода в положительном нап­равлении связываются воедино, дают в результа­те слово a₁ A ₁… A_n a₂. Это слово называется результатом дерева вывода.

Пример 1.3. Выводам слова (())() в G и G ’ соответствуют деревья вывода:

 

 

Пунктирные линии не принадлежат дереву вывода, которое соответст­вует правилу вывода в примере. Тем не менее дерево, состоящее из сплошных и пунктирных линий, также является деревом вывода с резуль­татом (())(). Таким образом, имеется два различных дерева вывода с ре­зультатом (())(). Это приводит к определению однозначной контекстно-свободной грамматики. Контекстно-свободная грамматика G называется однозначной тогда и только тогда, когда для каждого w Î L (G) найдется единственное дерево вывода. В противном случае она называется много­значной.

Пример 1.4. Пусть G = (Ф, S, P, S),

где Ф = { оператор if , оператор };

S = { if, then, else, выражение, другой_оператор };

P = { оператор if ::= if выражение then оператор |

if выражение then оператор else оператор ;

оператор ::= оператор if | другой_оператор };

S = оператор if .

L (G) описывает оператор if в PASCAL. Грамматика G – неоднозначна, так как «программа»:

if выражение then if выражение then
другой_оператор else другой_оператор

имеет два различных дерева вывода. Необходимая для языка программи­рования однозначность грамматики достигается тем, что вышеуказанная программа ставится в соответствие всегда только одному из двух возмож­ных деревьев вывода. □

Контекстно-свободные грамматики, продукции которых имеют про­стую структуру, называются регулярными грамматиками. Контекстно-сво­бодная грамматика G = (Ф, S, P, S) называется регулярной, если все про­дукции имеют вид: А ® аВ ‚ А ® а ‚ или S ® ε‚ А ‚ В ÎΦ‚ а ÎS. Однако про­дукция S ® ε может встречаться только тогда, когда S не встречается нигде в правой части продукции. Таким образом, продукции вида А ® aS запре­щены.

Формальный язык L Í S^* называется регулярным, если существует ре­гулярная грамматика G, такая что L (G) = L. Отсюда сразу следует, что ка­ждый регулярный язык также контекстно-свободный. Однако обратное не­верно: именно { aⁿbⁿ | n 1} контекстно-свободный, но не регулярный язык. Позже мы увидим, что множество всех констант в PASCAL – регулярный язык (см. пример 1.11).

Пример 1.5. Контекстно-свободная грамматика.

G = ({ E, T }, {+,*, a }, P, E), где P = { E Ε + T, E T, T T * a, T ® a }

порождает язык L (G) = a (* a)^*(+ a (* a)^*)^*. Поэтому возможны следующие продукции:

Е Þ^* T + T +...+ T, T Þ^* a * a * ... * a.

Слова из L (G) могут рассматриваться как арифметические выражения без скобок. Однако возможно указать некоторую регулярную грамматику G ’, которая порождает L (G), именно: G ^’= ({ S, A }, {+,*, a }, P ’, S), где P ’ = { S аА ‚ S а ‚ А + S, A * S }. Тогда L (G) регулярный язык. □

Разберем теперь проблему анализа некоторого заданного слова w отно­сительно грамматики G. Под этим понимается следующее.

Пусть G = (Ф, S, P, S) и w ÎS^*. Тогда требуется проверить, является ли w словом из L (G). Эта проблема встречается при трансляции программ. В случае, если L (G) – множество всех синтаксически правильных программ и w – программа, то требуется проверить, является ли w синтаксически пра­вильной программой, то есть лежит ли w в L (G). Мы увидим, что конечные автоматы (соответственно, магазинные автоматы) могут применяться для разрешения проблемы анализа в отношении регулярных (соответственно, контекстно-свободных грамматик).

Конечный автомат обладает конечным числом состояний и входной лентой со считывающей головкой. Если конечный автомат находится в не­котором состоянии и считывающая головка читает символ на входной ленте, то функция перехода недетерминировано в зависимости от преды­дущего состояния и прочитанного символа определяет новое состояние и считывающая головка смещается на один символ вправо. Конечный авто­мат имеет, кроме того, одно начальное состояние и сколь угодно много ко­нечных состояний. Некоторое слово воспринимается конечным автоматом тогда и только тогда, когда это слово как содержимое входной ленты пере­водит конечный автомат из начального состояния в некоторое конечное состояние. В общем случае конечный автомат работает недетерминиро­вано. Существует несколько возможных определений конечных автоматов.

Конечный автомат A над алфавитом есть система A =(Q, S, d, q₀, F),

(i)

где:

Q – конечное непустое множество состояний;

(ii) S – входной алфавит;

(iii) d: Q ´S ® P(Q) (степень множества Q) – функция перехода;

(iv) q₀ Î Q – начальное состояние;

(v) F Í Q – множество конечных состояний.

Продолжим отображение dдо отображения : Q ´S^* ®P(Q) путем

(q, e) = { q }, (q, aw) = для каждого q Q, w ÎS^*, a ÎS.

Слово w принимается конечным автоматом A тогда и только тогда, ко­гда F Ç (q ₀, w) ¹ Æ. Формальный язык ||A||, принимаемый автоматом A, есть ||A|| = { w | F Ç (q ₀, w) ¹ Æ}.

В случае, если не возникает путаницы, вместо пишут просто d.

Функцию перехода d можно также представить так называемой табли­цей переходов.

Пусть A = (Q, S, d, q₀, F), где Q = { q ₀, q ₁, …, q_n } и S = { a ₁, a ₂, …, a_m }, тогда d изображается следующей таблицей:

 

d	a 1	a 2	…	am
q 0	d(q 0, a 1)	d(q 0, a 2)	…	d(q 0, am)
q 1	d(q 1, a 1)	d(q 1, a 2)	…	d(q 1, am)
.	.	.		.
.	.	.		.
.	.	.		.
qn	d(qn, a 1)	d(qn, a 2)	…	d(qn, am)

 

Другая возможность – представление функции перехода ориентирован­ным помеченным графом. Граф имеет n +1 узлов, которые соответствуют состояниям q ₀,…, q_n. Если выполняется q d(p, a), то ребро, обозначенное символом а, ведет от узла p к узлу q. Узел, соответствующий начальному состоянию, обозначается зачерненным, а узлы, соответствующие конеч­ным состояниям, заключаются в кольцо.

Слово a ₁… a_m ÎS^* описывает путь от p к q в графе, в случае если сущест­вуют узлы p ₁ = p, p ₂,…, p_m, p_{m +1} = q, так, что для каждого j, 1 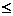j 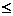m, имеется ребро от p _j к p_{j +1}, которое обозначается как a_j. Пустое слово e описывает для любого q путь от q к q. Поэтому справедливо, что слово w ÎS^* в точно­сти тогда описывает путь в графе от p к q, когда q Î (p, w). Отсюда ||A|| – множество всех слов, которые описывают путь от начального состояния к одному из конечных состояний.

Пусть G = (Ф, S, P, S) – регулярная грамматика. Построим граф конеч­ного автомата, который воспринимает L (G).

Множество узлов графа задается как Ф È { F }. Узел F – конечный узел.

Если S ® eÎ R, то S также конечный узел. Начальный узел задается че­рез S.

Если A ® a Î R, то ребро, обозначенное через а, ведет от узла А к ко­неч­ному узлу F.

Если A ® aB Î R, то ребро а ведет от узла А к узлу В.

Пример 1.5. (продолжение). Построим граф конечного автомата, вос­принимающего L (G):

Конечный автомат A = (Q, S, d, q₀, F) – детерминированный, если |d(q, x)|£1 для всех q Q, x ÎS. Вместо d(q, x) = { p } пишем тогда d(q, x) = p, что оз­начает, что мы рассматриваем d как частичную функцию d: Q ´S ® Q. Оп­ределение для упрощается тогда до следующего:

(q, ε) = q, (q, aw) = (d(q, a), w) и ||A|| = { w | (q₀, w)Î F }.

На графе это означает, что от каждого узла q отходит не более чем одно ребро, обозначаемое х ÎS.

Справедлива следующая теорема:

Пусть A = (Q, S, d, q₀, F) – конечный автомат, тогда имеется детер­минированный конечный автомат A’, такой что ||A|| = ||A’||.

Мы хотим теперь построить автомат A’ с множеством состояний P (Q). Продолжим d: Q ´S® P (Q) до отображения d’: P (Q) ´S ® P (Q) посред­ством

d′({ q ₁, q ₂,..., q_k }, x) = (q_j, x), q ₁,..., q_k Q, x ÎS.

Таким образом, d’({ q ₁, q ₂,..., q_k }, x) есть множество всех тех состояний, которые могут быть достигнуты из одного из состояний q ₁, q ₂,..., q_k через ребро, обозначенное x. Пусть F ’ = { G P (Q) | G F ≠ Ø}, что значит множе­ство G как состояние автомата A’ есть конечное состояние тогда и только тогда, когда оно содержит хотя бы одно конечное состояние из F. Пусть A’ = (P (Q), S, d’, { q₀ }, F ’). Тогда выполняется ||A’|| = ||A|| и A’ по по­строению – детерминированный автомат.

Пример 1.5. (продолжение). Построим граф детерминированного ко­нечного автомата, который принимает L (G):

С помощью детерминированных конечных автома­тов можно конечно «быстро» анализировать регуляр­ные языки. Обратно: можно показать, что для каждого конечного автомата A найдется регулярная грамма­тика G, та­кая что L (G) = ||A||.

Предложение 1.1. Пусть L Í S^* – формальный язык. Тогда следующие высказывания эквивалентны:

(i) существует регулярная грамматика G, такая что L = L (G);

(ii) существует конечный автомат A, такой что L = ||A||;

(iii) существует детерминированный конечный автомат, такой что L = ||A||. □

Пример 1.6. Слово v ÎS^* называется подсловом слова w ÎS^* тогда и только тогда, когда найдутся слова u ₁, u ₂ÎS^*, такие, что w = u ₁ v u ₂. Требу­ется проверить, встречаются ли в слове w ÎS^* подслова с определенными свойствами. Для этого строят детерминированный конечный автомат A, который принимает все слова w ÎS^*, содержащие подслова с определен­ными свойствами. Это есть простейшая проблема распознавания образов («сопоставление с образцом»).

Пусть S = { a, b }. Требуется проверить, обладает ли слово w ÎS^* сле­дующими свойствами:

(i) ааа должно быть подсловом слова w;

(ii) аa должно встречаться как подслово на правом конце слова w.

Таким образом, можно построить детерминированный конечный авто­мат, который принимает формальный язык L ={ a,b }^* ааа { a, b }^*Ç{ a,b }^* аа. Укажем две возможных конструкции.

Первый способ построения: конечный автомат вида

 

принимает L. Чтобы его «детерминировать» представим функцию пере­хода в виде таблицы (без фигурных скобок) и определим функцию пере­хода детерминированного автомата.

 

	a	b
q0	q0, q1	q0
q1	q2	–
q2	q3	–
q3	–	q4
q4	q4, q5,	q4
q5	q6	–
q6	–	–
q0, q1	q0, q1, q2	q0
q0, q1, q2	q0, q1, q2, q3	q0
q0, q1, q2, q3	q0, q1, q2, q3	q0, q4
q0, q4	q0, q1, q4, q5	q0, q4
q0, q1, q4, q5	q0, q1, q2, q4,q5, q6	q0, q4
q0, q1, q2, q4, q5, q6	q0, q1, q2, q3,q4,q5,q6	q0, q4
q0, q1, q2, q3, q4, q5, q6	q0, q1, q2, q3, q4, q5, q6	q0, q4

 

Это дает следующий детерминированный конечный автомат:

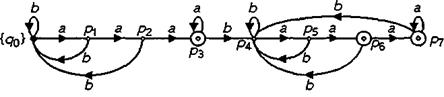
Относительно состояний p₃, p₆, p₇ видно следующее: три состояния явля­ются конечными состояниями. Символ a переводит автомат из одного из этих трех состояний снова в одно из трех состояний; символ b переводит из всех трех состояний в состояние p₄. Поэтому можно три состояния p₃, p₆, p₇ объединить в одно состояние p, при этом получают следующий де­терминированный автомат:

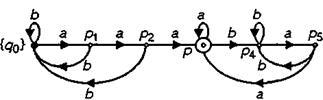
Второй способ построения. Видно, что слово лежит в L тогда и только то­гда, когда оно заканчивается на aaa или содержит aaa и заканчивается на aa:

Затем дополняют этот «скелет автомата» до вышеописанного автомата. 

 

Обратимся к магазинным автоматам.

Магазин – это накопитель, в котором может читаться или изменяться только самый верхний символ.

Магазинный автомат имеет конечное число состояний, входную ленту со считывающей головкой и магазинную ленту (стек) с головкой чтения-записи, которая находится над самым верхним магазинным символом. Если магазинный автомат находится в некотором состоянии, читающая головка читает символ с входной ленты и головка чтения-записи читает самый верхний символ на магазинной ленте, то функция перехода опреде­ляет недетерминированным образом, в зависимости от старого состояния и двух прочитанных символов, следующие действия:

1) читающая головка остается над прочитанным символом или пе­редвигается на один символ вправо;

2) самый верхний символ в магазине стирается;

3) слово над алфавитом магазина записывается на магазинной ленте, и головка чтения-записи устанавливается на новый самый верхний символ магазинной ленты;

4) магазинный автомат переходит в новое состояние.

Итак, пусть дан магазинный автомат, работающий с входным алфави­том S. На входной ленте пусть записано слово w ÎS^*. Магазинный автомат стар­тует в заданном начальном состоянии, имеет читающую головку над пер­вым символом входного слова и головку чтения-записи над стартовым сим­волом в остальной части пустой магазинной ленты. Далее, автомат действу­ет согласно пунктам 1) – 4). Если магазинному автомату удается попасть в так называемое конечное состояние, причем читающая головка должна сто­ять справа от последнего символа входной ленты, то тогда го­ворят, что ма­газинный автомат принимает w через конечное состояние. Если магазинно­му автомату удается достичь того, что магазинная лента пуста и читающая головка находится справа от последнего символа вход­ной ленты, то говорят, что магазинный автомат принимает w через пустой магазин.

Формализуем теперь магазинные автоматы.

Магазинный автомат P есть семерка P = (Q, S, G, d, q_0, p_0, F), где

(i) Q – непустое конечное множество состояний;

(ii) S – алфавит, называемый входным алфавитом;

(iii) G – алфавит, называемый алфавитом магазина;

(iv) q₀ Î Q – начальное состояние;

(v) p₀ ÎG – начальный символ на магазинной ленте;

(vi) F 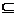Q – множество конечных состояний;

(vii) d: Q (SÈ{ e }) G® P _f (Q Г^*) – функция перехода.
(Через P _f мы обозначаем множество всех конечных подмножеств.)

Содержимое магазинной ленты есть слово, причем самый верхний символ магазина стоит крайним слева.

Интерпретация d следующая:

Пусть d(q,a,p)={ (q₁, g₁),…,(q_m, g_m) }, q,q₁,…,q_m Î Q, a Î S, p Î G, g₁, …, g_m ÎГ^*.

Если магазинный автомат находится в состоянии q, головка чтения чи­тает символ a, а головка чтения-записи читает самый верхний символ в ма­газине p, то магазинный автомат выбирает недетерминированным образом некоторую пару (q_i, g_i). Это означает, что магазинный автомат переходит в состояние q_i, на магазинной ленте p замещается на g_i, головка чтения пере­двигается на один символ вправо и головка чтения-записи устанавливается над самым верхним (первым) символом слова g_i.

Если выполняется d(q,e, p)={ (q₁, g₁),…,(q_m, g_m) }, то это означает, что головка чтения ничего не читает, а поэтому также и не перемещается вправо. Состояние и содержимое магазина изменяются, как описано выше.

Пусть P = (Q, S, G, d, q₀, p₀, F) – магазинный автомат. Конфигурация (си­туация) магазинного автомата P есть тройка (q, w, g), q Î Q, w ÎS^*, gÎГ^*. Ин­туитивно это означает, что автомат находится в состоянии q, что слово w – еще не прочитанная часть входного слова и что g стоит на магазинной ленте.

Определим далее отношение _P, называемое прямым отношением пе­рехода над конфигурациями P:

(q₁, aw, pg) _P (q₂, w, g₁g) Û (q₂, g₁)Îd(q₁, a, p)
для q₁, q₂ Î Q, a ÎSÈ{ e }, w ÎS^*, p ÎG, g, g₁ ÎG^*

Отношение _P^* есть рефлексивное и транзитивное замыкание _P. Если выполняется (q₁, w₁, g₁) _P^* (q₂, w₂, g₂), то говорят, что конфигурация (q₁, w₁, g₁) ведет к (q₂, w₂, g₂). В случае, если ясно, какой магазинный автомат имеется в виду, вместо _P и _P^*можно писать  и ^*.

Пусть P = (Q, S, G, d, q₀, p₀, F) – магазинный автомат. Язык T(P), кото­рый принимается автоматом P через конечное состояние, есть

T(P)={ w ½(q₀, w, p₀) ^* (q,e, g), qÎF, gÎG^*}.

Язык N(P), который принимается автоматом P через пустой магазин, есть

N(P)={ w ½(q₀, w, p₀) ^* (q, e,e), qÎQ }.

Язык , который принимается автоматом P через пустой магазин и конеч­ное состояние,есть

= { w ½(q₀, w, p₀) ^* (q, e,e), qÎF }.

Конечный автомат P – детерминированный тогда и только тогда, когда для всех qÎQ, a ÎSÈ{ e }, p ÎG выполнено:

1) ½d(q, a, p)½£ 1;

2) если d(q, e, p) ¹ Æ, то d(q, x, p) =Æ для всех x ÎS.

Магазинный автомат P = (Q, S, G, d, q_0, p₀, F) может быть представлен бес­конечным ориентированным помеченным графом: множество узлов графа задается как {(g, q)½ gÎG^*, q ÎQ}. От узла (g_1, q₁) к узлу (g_2, q₂) ведет в точ­ности одно ребро, обозначенное a ÎSÈ e, если

(q_1,a, g₁)  (q₂, e, g₂), т. е., если g₁ = pg, g₂ = g₃g и (q₂, g₃) Î d(q_1,a, p).

Тогда справедливо, что w ÎS^* в точности тогда описывает путь от (g_1, q₁) к (g_2, q₂), когда (q_1,w, g₁) ^* (q₂, e, g₂).

Отсюда следует непосредственно, что T (P) есть множество всех тех слов, которые описывают путь от (p₀,q₀) к (g, q), q Î F, gÎG^*; что N (P) есть множе­ство всех слов, описывающих путь от (p₀,q₀) к (e, q), qÎQ и что есть мно­жество всех тех слов, которые описывают путь от (p₀,q₀) к (e, q), q Î F.

Пусть G =(F,S, R, S) – контекстно-свободная грамматика, тогда магазин­ный автомат P = ({q},S, V,d, q,S,{ q }) принимает язык L(G) через пустой ма­газин (и конечное состояние), причем d определена следующим образом:

 

(q, Ba) Î d(q, e, A) A ® Ba Î P, B Î F,

(q, a) Î d(q, a, A) A ® aa Î P, a Î S,

(q, e) Î d(q, e, A) A ® e Î P,

d(q, x, x) = {(q, e)} для всех x ÎS.

 

Пример 1.7. Для контекстно-свободной грамматики G = ({ S },{ a, b },{ S ® aSS, S ® b }, S) получают P = ({ q },S, V,d, q, S,{ q }), где d(q, e, S)={(q, aSS),(q, b)}, d(q, a, a)=d(q, b, b)={(q, e)}. Имеем: