Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задач трехмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трех изобразить графически вообще невозможно.
Пусть задача линейного программирования задана в двумерном пространстве, т. е. ограничения содержат две переменные.
Если в ЗЛП ограничения заданы в виде неравенств с двумя переменными, она может быть решена графически. Графический метод решения ЗЛП состоит из следующих этапов.
Этап 1.
Сначала на координатной плоскости x1Ox2 строится допустимая многоугольная область (область допустимых решений, область определения), соответствующая ограничениям:
1.6)
Не приводя строгих доказательств, укажем те случаи, которые тут могут получится.
1. Основной случай - получающаяся область имеет вид ограниченного выпуклого многоугольника (рис. 1а).
2. Неосновной случай получается неограниченный выпуклый многоугольник, имеющий вид, подобный изображенному на рис. 1б. Подобная ситуация, например, получится, если в рассмотренном выше примере убрать ограничение х1 + х 2 ≤ 3. Оставшаяся часть будет неограниченным выпуклым многоугольником.
|
|
|
Наконец, возможен случай, когда неравенства (1.6) противоречат друг другу, и допустимая область вообще пуста.
Рассмотрим теорию на конкретном примере:
Найти допустимую область задачи линейного программирования, определяемую ограничениями
1.32)
Решение:
1. Рассмотрим прямую –x1+x2 = 1. При x1 = 0, x2 = 0, а при x2= 0, x1= -1. Таким образом, эта прямая проходит через точки (0,1) и (-1,0). Беря x1 = x2 = 0, получим, что -0+0<1 и поэтому интересующая нас полуплоскость лежит ниже прямой, изображенной на рис. 4.а.
2. Рассмотрим прямую 
. При 
, а при. Таким образом, эта прямая проходит через точки (0, -1/2) и (1,0). так как 
(4.б).
3. Наконец, рассмотри 
м прямую 
. Она проходит через точки (0,3) и (3,0) и так как 0+0<3, то интересующая нас полуплоскость лежит ниже прямой, изображенной на рис. 4.в.
Сводя все вместе и добавляя условия х1 ≥ 0,х2 ≥ 0 получим рисунок 5, где выделена область, в которой выполняются одновременно все ограничения (1.32). Обратим внимание на то, что получившаяся область имеет вид выпуклого многоугольника.
Этап 2.
Вернёмся теперь к исходной задаче линейного программирования. В ней, кроме системы неравенств, есть еще целевая функция с1х1+с2х2 =>max.
|
Рассмотрим прямую с1х1+с2х2 = L. Будем увеличивать L. Что будет происходить с нашей прямой?
Легко догадаться, что прямая будет двигаться параллельно самой себе в том направлении, которое дается вектором (с1,с2), так как это вектор нормали к нашей прямой и одновременно вектор градиента функции
f(х1,х2) = с1х1+с2х2 .
А теперь сведем всё вместе. Итак, надо решить задачу
Ограничения задачи вырезают на плоскости некоторый многоугольник. Пусть при некотором L прямая с1х1+с2х2 = L пересекает допустимую область. Это пересечение дает какие-то значения переменных (х1,х2), которые являются планами.
Этап 3
Увеличивая L мы начнем двигать нашу прямую и её пересечение с допустимой областью будет изменяться (см. рис. 7). В конце концов эта прямая выйдет на границу допустимой области как правило, это будет одна из вершин многоугольника. Дальнейшее увеличение L приведёт к тому, что пересечение прямой с1х1+с2х2 = L с допустимой областью будет пустым. Поэтому то положение прямой с1х1+с2х2 = L, при котором она вышла на граничную точку допустимой области, и даст решение задачи, а соответствующее значение L и будет оптимальным значением целевой функции.
Рис. 7 II. ПРАКТИЧЕСКИЙ РАЗДЕЛ
Задача №1
Для производства двух видов изделий А и В предприятие использует три вида сырья. Другие условия задачи приведены в таблице 1.1..
Таблица 1.1.
| Вид сырья |  Нормы расхода сырья на одно изделие, кг
 A B
| Общее количество сырья, кг |
| I | 12 4 | |
| II | 4 4 | |
| III | 3 12 | |
| Прибыль от реализации одного изделия, ден. ед. | 30 40 | ? |
Составить такой план выпуска продукции, при котором прибыль предприятия от реализации продукции будет максимальной при условии, что изделие В надо выпустить не менее, чем изделия А.
Решение.
Обозначим через х1 и х2 количество единиц продукции соответственно А и В, запланированных к производству. Для их изготовления потребуется (12 х1 +4 х2) единиц ресурса I, (4х1 +4х2) единиц ресурса II, (3х1 +12х2) единиц ресурса III. Так как, потребление ресурсов I, II, III не должно превышать их запасов, то связь между потреблением ресурсов и их запасами выразится системой неравенств:
12х1 +4х2 ≤ 300; 
3х1 + х2 ≤ 75;
4х1 +4х2 ≤ 120; х1 + х2 ≤ 30;
3х1 +12х2 ≤ 252. х1 +4х2 ≤ 84.
По смыслу задачи переменные х1 ≥ 0, х2 ≥0. (1,1)
Конечную цель решаемой задачи – получение максимальной прибыли при реализации продукции – выразим как функцию двух переменных х1 и х2.
Суммарная прибыль А составит 30х1 от реализации продукции А и 40х 2 от реализации продукции В, то есть: F = 30х1 +40х 2. (1,2)
Изобразим многоугольник решений данной задачи.
В ограничениях задачи поменяем знаки неравенства на знаки равенства.
Проведем оси: на горизонтальной будут указываться значения переменной х1, а на вертикальной — х2.Далее рассмотрим условие неотрицательности переменных: x1 ≥ 0 и х2 ≥ 0. Эти два ограничения показывают, что пространство допустимых решений будет лежать в первом квадранте (т.е выше оси x1 и правее оси х2).
Чтобы учесть оставшиеся ограничения, проще всего заменить неравенства на равенства, в результате чего получится система уравнений прямых:
3х1 + х2 = 75;
х1 + х2 = 30;
х1 +4х2 = 84.
а затем на плоскости провести эти прямые.
Например, неравенство 3х1 + х2 ≤ 75 заменяется уравнением прямой 3х1 + х2 = 75. Чтобы провести эту линию, надо найти две различные точки, лежащие на этой прямой Можно положить х1 = 0, тогда х2 = 75/1 = 75.. Аналогично для х2 = 0 находим x1 = 75/3 = 25. Итак, наша прямая проходит через две точки (0, 75) и (25;0). Аналогично найдём остальные точки и запишем их в таблицу 1.2..
Таблица 1.2.
| 3х1 +х2 ≤ 75; | х1 +х2 ≤ 30; | х1 +4х2 ≤ 84. | |||
| х1 | х2 | х1 | х2 | х1 | х2 |
Согласно данной таблицы, построим график в программе Excel.
Заштрихованная область, изображённая на рисунке, является областью допустимых значений функции F. Т.к. целевая функция F стремиться к max, то идя по направлению вектора n, получим точку B с оптимальным решением. Для определения ее координаты возьмем две прямые, на пересечении которых она образуется:
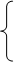
3х1 + х2 ≤ 75, х1 = 19,64,
х1 + 4х2 ≤ 84, х2 = 16,09., т. е. B(16,09; 19,64)
максимальное значение линейной функции равно:
Fmax = 30*16,09 + 40*19,64 = 1232,80.
Итак, Fmax = 1232,80 при оптимальном решении х1 = 16,09, х2 = 19,64, т. е. максимальная прибыль в 1232,80 ден. ед. может быть достигнута при производстве 16,09 единиц продукции А и 19,64 единиц продукции В.
Ответ: Fmax = 1232,80.
Задача № 2
Для изготовления двух видов продукции Р1 и Р2 используют три вида сырья: S1, S2, S3. Запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также величина прибыли, получаемая от реализации единицы продукции, приведены в таблице 2.1.
Таблица 2.1.
| Вид сырья | Запас сырья | Количество единиц сырья, идущих на изготовление единицы продукции | |
| Р1 | Р2 | ||
| S1 | |||
| S2 | |||
| S3 | |||
| Прибыль от единицы продукции, руб. |
Необходимо составить такой план выпуска продукции, чтобы при ее реализации получить максимальную прибыль.
Решение.
Обозначим через х1 количество единиц продукции Р1, а через х2 – количество единиц продукции Р2. Тогда, учитывая количество единиц сырья, расходуемое на изготовление продукции, а так же запасы сырья, получим систему ограничений:
2х1 + 5х2 ≤ 20
8х1 + 5х2 ≤ 40
5х1 + 6х2 ≤ 30
которая показывает, что количество сырья, расходуемое на изготовление продукции, не может превысит имеющихся запасов. Если продукция Р1 не выпускается, то х1=0; в противном случае x1 = 0. То же самое получаем и для продукции Р2. Таким образом, на неизвестные х1 и х2 должно быть наложено ограничение неотрицательности: х1 ≥ 0, х2 ≥ 0.
Конечную цель решаемой задачи – получение максимальной прибыли при реализации продукции – выразим как функцию двух переменных х1 и х2. Реализация х1 единиц продукции Р1 и х2 единиц продукции Р2 дает соответственно 50х1 и 40х2 руб. прибыли, суммарная прибыль Z = 50х1 + 40х2 (руб.)
Условиями не оговорена неделимость единица продукции, поэтому х1 и х2 (план выпуска продукции) могут быть и дробными числами.
Требуется найти такие х1 и х2, при которых функция Z достинает максимум, т.е. найти максимальное значение линейной функции Z = 50х1 + 40х2 при ограничениях
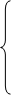2х1 + 5х2 ≤ 20
8х1 + 5х2 ≤ 40
5х1 + 6х2 ≤ 30
х1 ≥ 0, х2 ≥ 0.
Изобразим многоугольник решений данной задачи.
В ограничениях задачи поменяем знаки неравенства на знаки равенства.
Построим в программе Excel таблицы нахождения точек пересечения линий с осями координат (Рисунок 1) и график (Рисунок 2).
Рисунок 1.
Рисунок 2.
Заштрихованная область, изображённая на рисунке, является областью допустимых значений функции Z. Т.к. целевая функция Z стремиться к max, то идя по направлению вектора n, получим точку C с оптимальным решением. Для определения ее координаты возьмем две прямые, на пересечении которых она образуется:
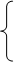
8х1 + 5х2 ≤ 40 х1 = 3,91,
5х1 + 6х2 ≤ 30, х2 = 1,74., т. е. C(3,91; 1,74)
максимальное значение линейной функции равно:
Zmax = 50*3,91 + 40*1,74 = 265,10.
Итак, Zmax = 265,10 при оптимальном решении х1 = 3,91, х2 = 1,74, т. е. максимальная прибыль в 1232,80 ден. ед. может быть достигнута при производстве 3,91единиц продукции P1 и 1,74 единиц продукции P2.
Ответ: Zmax = 265,10.
Задача № 3
| Питательные вещества | Число единиц питательных веществ в 1 кг корма | Необходимый минимум питательных веществ | |
| A | B | ||
| S1 | |||
| S2 | |||
| S3 | |||
| Минимальная стоимость за 1 кг корма, в руб.. | ? |
Имеется два вида корма. A и B, содержащие вещества(витамины) S1, S2, S3. Содержание числа единиц питательных веществ в одном кг каждого вида корма и необходимый минимум самих питательных веществ даны в таблице:
Решение:
Пусть х1 и х2 – количество кормов вида А и В соответственно. В одном килограмме каждого вида корма содержится (3х1 + х2) единиц питательного вещества S1, (x1 + 2x2) - S2 и (x1 + 6x2) - S3. Так количество питательных веществ не должно быть меньше необходимого минимума, то запишем следующую систему неравенств:
3х1 + х2 ≥ 8,
x1 + 2x2 ≥ 9,
x1 + 6x2 ≥ 12,
x1, x2 ≥ 0.
Минимальную стоимость витаминов за 1 кг корма, выразим следующей функцией: F = 4x1 + 6x2 => min.
Изобразим многоугольник решений данной задачи.
В ограничениях задачи поменяем знаки неравенства на знаки равенства.
Построим в программе Excel таблицы нахождения точек пересечения линий с осями координат (Рисунок 1) и график (Рисунок 2).
Рисунок 1.
Рисунок 2.
Выделенная область, изображённая на рисунке, является областью допустимых значений функции F. Точка В - оптимальное решение. Для определения ее координаты возьмем две прямые, на пересечении которых она образуется:
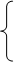
x1 + 2x2 = 9, x1 = 7,50,
x1 + 6x2 = 12, x2 = 0,75.
Минимальное значение линейной функции равно:
Fmin = 4*7.5 + 6*0.75 = 34.50.
Итак, Fmin = 34.50 при оптимальном решении х1 = 7.50, х2 = 0.75.
Ответ: Fmin = 34,50.
Задача № 4
Трикотажная фабрика использует для производства свитеров и кофточек шерсть, силикон и нитрон, запасы которых составляют 820, 430 и 310 кг. Количество пряжи каждого вида (в кг), необходимой для изготовления одного изделия, а также прибыль, получаемая от их реализации, приведены в таблице.
| Вид сырья. | Нормы расхода пряжи. | Запас | |
| Свитера. | Кофточки. | ||
| Шерсть | 0,4 | 0,2 | |
| Силон | 0,2 | 0,1 | |
| Нитрон | 0,1 | 0,1 | |
| Прибыль | 7,8 | 5,6 | ? |
Определить план выпуска изделий, максимизирующий прибыль.
Решение.
Пусть х1 и х2 – норма расхода пряжи для свитеров и кофточек соответственно. Количество пряжи каждого вида (в кг), необходимой для изготовления одного изделия запишем в следующую систему неравенств:
0,4х1 + 0,2х2 ≤ 820,
0,2x1 + 0,1x2 ≤ 430,
0,1x1 + 0,1x2 ≤ 310,
x1, x2 ≥ 0.
Максимальная прибыль от реализации свитеров и кофточек выразим следующей функцией: F = 7,8x1 + 5,6x2 => max.
Изобразим многоугольник решений данной задачи.
В ограничениях задачи поменяем знаки неравенства на знаки равенства.
Построим в программе Excel таблицы нахождения точек пересечения линий с осями координат (Рисунок 1) и график (Рисунок 2).
Рисунок 1.
Рисунок 2.
Выделенная область, изображённая на рисунке, является областью допустимых значений функции F. Точка В - оптимальное решение. Для определения ее координаты возьмем две прямые, на пересечении которых она образуется:
0,4x1 + 0,2x2 = 820, x1 = 1000,
0,1x1 + 0,1x2 = 310, x2 = 2100.
Максимальное значение линейной функции равно:
Fmax = 7.8*1000 + 5.6*2100 = 19560.
Итак, Fmax = 19560 при оптимальном решении х1 = 1000, х2 = 2100.
Ответ: Fmax = 19560.
Задача № 5
На звероферме могут выращиваться чёрно-бурые лисицы и песцы. Для обеспечения нормальных условий их выращивания используются три вида кормов. Определить, сколько лисиц и песцов следует выращивать на звероферме, чтобы прибыль от реализации их шкурок была максимальной.
| Вид корма. | Кол-во единиц корма, которое должны получать. | Общее кол-во корма | |
| Лисица | Песец. | ||
| I | |||
| II | |||
| III | |||
| Прибыль | ? |
Решение:
Пусть х1 и х2 – количество единиц корма, которые должны получать лисиа и песец, соответственно. Количество единиц каждого вида корма, необходимого для выращивания одного животного запишем в следующую систему неравенств:
2х1 + 3х2 ≤ 180,
4x1 + 1x2 ≤ 240,
6x1 + 7x2 ≤ 426,
x1, x2 ≥ 0.
Максимальная прибыль от реализации шкурок выразим следующей функцией: F = 16x1 + 12x2 => max.
Изобразим многоугольник решений данной задачи.
В ограничениях задачи поменяем знаки неравенства на знаки равенства.
Построим в программе Excel таблицы нахождения точек пересечения линий с осями координат (Рисунок 1) и график (Рисунок 2).
Рисунок 1.
Рисунок 2.
Выделенная область, изображённая на рисунке, является областью допустимых значений функции F. Точка С - оптимальное решение. Для определения ее координаты возьмем две прямые, на пересечении которых она образуется:
x2 = 0, x1 = 60,
4x1 + x2 = 240, x2 = 0.
Максимальное значение линейной функции равно:
Fmax = 16*60 + 12*0 = 960.
Итак, Fmax = 960 при оптимальном решении х1 = 60, х2 = 0.
Ответ: Fmax = 960.
Заключение
В данной курсовой работе мною были освоены навыки решения задач линейного программирования геометрическим методом. Для этого я изучила теоретические сведения, необходимые для решения задач линейного программирования указанным методом. Я узнала, что данный метод применяется в основном при решении задач двумерного пространства и только некоторых задач трехмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трех изобразить графически вообще невозможно. Также я узнала, как строятся прямые на плоскости, для чего разобрала основные понятия линейной алгебры и выпуклого анализа. После чего, рассмотрела все этапы геометрического решения задач линейного программирования, благодаря чему я узнала, что бывают разные случаи при решении задач, а именно:
1) Основной случай, когда полученная область образует ограниченный выпуклый многоугольник;
2) Неосновной случай, когда полученная область образует неограниченный выпуклый многоугольник;
3) И также, возможен случай, когда неравенства противоречат друг другу, и допустимая область пуста, то есть данная задача не будет иметь решений.
В первых двух случаях задача может иметь единственное решение в конкретной точке, а также в любой точке отрезка или луча.
Таким образом, освоив все необходимые навыки использования геометрического метода для решения задач линейного программирования, я решила поставленные задачи.
Список литературы
1. Коротков М., Гаврилов М. «Основы линейного программирования», 2003 г..
2. Филькин Г.В., «Линейное программирование» (лекции), Шахты, 2007 г..
3. Воротницкий Ю.И. «Исследование операций».
4. Теха Х. «Введение в исследование операций», Издательский дом «Вильямс», 2001 г..
5. Давыдов Э.Г. «Исследование операций», 1990 г..
6. Дегтярев Ю.И. «Исследование операций», 1986 г..
7. Алабин Б.К. «Методы исследования операций» (курс лекций).
8. Лищенко «Линейное и нелинейное программирование», М. 2003 г..
9. А.Н. Карасев, Н.Ш. Кремер, Т.Н. Савельева «Математические методы в экономике», М. 2000 г..
10. Мину М. Математическое программирование. Теория и алгоритмы. М. 2004 г..