Практическое занятие 2.
Определение характеристик случайных величин.
1. Расчет плотности вероятности.
2. Расчет среднего значения величины.
3. Расчет дисперсии.
4. Расчет среднего квадратичного отклонения.
Задача 1.1.
Случайная величина X задана плотностью распределения вероятности

Найти интегральную функцию F(x).
Решение.
1. f(x) - плотность распределения (плотность распределения вероятностей, плотность, дифференциальная функция распределения) случайной величины X:
 .
.
2. F (x) - функция распределения (функция распределения вероятностей, интегральная функция распределения) случайной величины X:
 .
.
3. Используем формулу:  .
.
Если  , то
, то  .
.
Если  , то
, то  .
.
Если  , то
, то 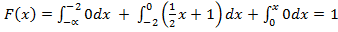
4. Итак,

Задача 2.1.
Случайная величина X задана функцией распределения F (x)
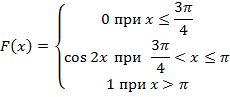
Требуется:
а) найти плотность распределения f (x),
б) найти математическое ожидание и дисперсию X.
Решение.
1. Учитывая, что 
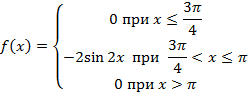
2. 
3. 
Задача 3.1. Дискретная случайная величина Х, имеющая смысл числа курьеров, задействованных для доставки корреспонденции в коммерческой организации, задана законом распределения:
| Х | ||||
| Р | 0,4 | 0,1 | 0,3 | 0,2 |
Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.
Решение.
1. Так как случайная величина является дискретной, то для вычисления М(Х) воспользуемся формулой. Имеем:

2. Найдем дисперсию D(x). Предварительно найдем математическое ожидание от х 2:

3. Далее получаем

4. Найдем среднее квадратическое отклонение. Имеем
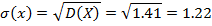
5. Таким образом, среднее число курьеров равно 1,3 со средним разбросом 1,22.
Практическое занятие 2.
Определение характеристик случайных величин.
Вариант №1
1. Расчет плотности вероятности.
2. Расчет среднего значения величины.
3. Расчет дисперсии.
4. Расчет среднего квадратичного отклонения.
Задача 1.
Случайная величина X задана плотностью распределения вероятности

Найти интегральную функцию F(x).
Задача 2.
Случайная величина X задана функцией распределения F (x)

Требуется:
а) найти плотность распределения f (x),
б) найти математическое ожидание и дисперсию X.
Задача 3. Дискретная случайная величина Х, имеющая смысл числа курьеров, задействованных для доставки корреспонденции в коммерческой организации, задана законом распределения:
| Х | ||||
| Р | 0,7 | 0,1 | 0,1 | 0,1 |
Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.
Практическое занятие 2.
Определение характеристик случайных величин.
Вариант №2
1. Расчет плотности вероятности.
2. Расчет среднего значения величины.
3. Расчет дисперсии.
4. Расчет среднего квадратичного отклонения.
Задача 1.
Случайная величина X задана плотностью распределения вероятности

Найти интегральную функцию F(x).
Задача 2.
Случайная величина X задана функцией распределения F (x)

Требуется:
а) найти плотность распределения f (x),
б) найти математическое ожидание и дисперсию X.
Задача 3. Дискретная случайная величина Х, имеющая смысл числа курьеров, задействованных для доставки корреспонденции в коммерческой организации, задана законом распределения:
| Х | ||||
| Р | 0,2 | 0,6 | 0,1 | 0,1 |
Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.
Практическое занятие 2.
Определение характеристик случайных величин.
Вариант №3
1. Расчет плотности вероятности.
2. Расчет среднего значения величины.
3. Расчет дисперсии.
4. Расчет среднего квадратичного отклонения.
Задача 1.
Случайная величина X задана плотностью распределения вероятности
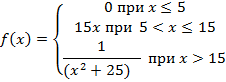
Найти интегральную функцию F(x).
Задача 2.
Случайная величина X задана функцией распределения F (x)

Требуется:
а) найти плотность распределения f (x),
б) найти математическое ожидание и дисперсию X.
Задача 3. Дискретная случайная величина Х, имеющая смысл числа курьеров, задействованных для доставки корреспонденции в коммерческой организации, задана законом распределения:
| Х | ||||
| Р | 0,3 | 0,2 | 0,4 | 0,1 |
Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.
Практическое занятие 2.