Законы Кирхгофа.
Для расчета любой электрической цепи необходимо задаться положительным направлением токов в ветвях. Рекомендуется в активных ветвях (содержащих источники) токи направлять по стрелке этого источника, а в пассивных ветвях – произвольно.
Различают 2 закона Кирхгофа:
1-й из них формулируется для узла,
2-й для замкнутого контура.
1-й закон Кирхгофа: в узле алгебраическая сумма токов равна нулю,
Или 2-я формулировка: сумма втекающих в узел токов равна сумме вытекающих.
 p – число ветвей, подходящих к узлу.
p – число ветвей, подходящих к узлу.
Для того, чтобы написать уравнение по I закону Кирхгофа, необходимо задаться положительным направлением токов в ветвях, и тогда, например, токи, входящие в узел, будем записывать с «+», а исходящие с «–» (или наоборот).
2-й закон Кирхгофа: в замкнутом контуре алгебраическая сумма ЭДС равна алгебраической сумме падений напряжения на пассивных элементах R, L, C.
 (R, L, C)
(R, L, C)
Для того, чтобы написать уравнение по IIзакону Кирхгофа, необходимо:
А) задаться положительным направлением токов в ветвях;
Б) выбрать направление обхода контура; при этом считается, что если стрелка ЭДС или направление тока через пассивный элемент совпадает с выбранным направлением обхода контура, то соответствующая ЭДС и падение напряжения (напряжение) на соответствующем пассивном элементе записываются со знаком «+» (каждый в своей части уравнения). В противном случае (если стрелка ЭДС и ток не совпадают с выбранным направлением обхода контура) – со знаком «–».
Расчет сложной цепи с помощью законов Кирхгофа.
Обозначим:
q – число узлов, p – число ветвей,
и тогда для каждой рассматриваемой цепи число уравнений, которое должно быть записано по законам Кирхгофа = р.
При этом число уравнений, которые нужно написать по IЗК = q-1, а соответственно по IIЗК = p-q+1.
q-1=2-1=1;
p-q+1=3-2+1=2.
Для записи уравнений по законам Кирхгофа необходимо задаться положительным направлением токов в ветвях и выбрать направление обхода каждого независимого контура.
Независимый контур – это контур, который отличается от других хотя бы одной ветвью.

Решив данную систему, получим искомые токи  ,
,  ,
,  .
.
К достоинству метода относится возможность определять непосредственно токи в ветвях.
К недостаткам – громоздкий математический аппарат (решение системы из большого числа уравнений).
8) Эквивалентные преобразования пассивных участков цепи.

9. Принцип и метод эквивалентного источника.
Метод основан на теореме об эквивалентном источнике.
Теорема: ток в любой ветви не изменится, если активный двухполюсник по отношению к рассматриваемой ветви заменить эквивалентным источником напряжения, ЭДС которого равна напряжению холостого хода на зажимах этой ветви, а внутренне сопротивление равно входному сопротивлению двухполюсника относительно этих же зажимов.
Двухполюсником называется цепь, рассмотренная по отношению к одной паре зажимов, называемой входом двухполюсника.
Метод эквивалентного источника особенно удобен, если нужно найти ток только в одной ветви.
Сущность метода заключается в том, что по отношению к ветви с искомым током, вся остальная часть цепи рассматривается как активный двухполюсник, и в расчетах может быть заменена одним эквивалентным реальным источником ЭДС, т.е. ветвью с последовательным соединением ЭДС и R. Дополняя эту ветвь ветвью с искомым током, получаем одноконтурную простую схему. Ток в этой схеме, следовательно, и искомый ток в ветви определяется по II закону Кирхгофа.
Возможны два случая:
1) Ветвь с искомым током – пассивная.


2) Ветвь с искомым током – активная.


В полученных выражениях неизвестны  и
и  .
.
Для определения  нужно рассматривать активную схему, которая получается из заданной путем удаления из нее ветви с искомым током. Определив в этой новой активной схеме напряжение
нужно рассматривать активную схему, которая получается из заданной путем удаления из нее ветви с искомым током. Определив в этой новой активной схеме напряжение  (холостого хода) относительно разомкнутых зажимов, к которым в исходной схеме подключена ветвь с искомым током, т.е. найдя напряжение
(холостого хода) относительно разомкнутых зажимов, к которым в исходной схеме подключена ветвь с искомым током, т.е. найдя напряжение  , мы тем самым найдем
, мы тем самым найдем  (на основании теоремы об эквивалентном источнике). Стрелку
(на основании теоремы об эквивалентном источнике). Стрелку  на разомкнутой ветви следует направить также, как направлена стрелка тока в исследуемой ветви.
на разомкнутой ветви следует направить также, как направлена стрелка тока в исследуемой ветви.
Для определения  рассматривают пассивную схему, которую получают из предыдущей, активной, устраняя из нее источники (закорачивание ветвей, содержащих идеальный источник ЭДС и разрывом ветвей с идеальным источником тока).
рассматривают пассивную схему, которую получают из предыдущей, активной, устраняя из нее источники (закорачивание ветвей, содержащих идеальный источник ЭДС и разрывом ветвей с идеальным источником тока).
Определив в этой пассивной цепи сопротивление относительно разомкнутых зажимов, к которым подключена ветвь с искомым током в исходной схеме, т.е найдя  , найдем
, найдем  (на основании теоремы об эквивалентном источнике).
(на основании теоремы об эквивалентном источнике).
Найденные выражения для  и
и  подставляем в формулы для токов.
подставляем в формулы для токов.
Переменный ток
 – мгновенное значение тока,
– мгновенное значение тока,
 – действующее значение тока,
– действующее значение тока,
 – амплитудное значение тока,
– амплитудное значение тока,
 – комплекс действующего значения тока,
– комплекс действующего значения тока,
 – комплекс амплитудного значения тока.
– комплекс амплитудного значения тока.
 ;
;
 ;
;  ;
;
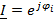 ;
; 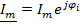 .
.
Комплексная форма расчета цепей переменного тока (см. конспект)
Закон Ома в комплексной форме

