Закон изменения и сохранения полной механической энергии.

Полной механической энергией системы тел называется сумма кинетической и потенциальной энергий:

E = Eк + Eп.

Изменение кинетической энергии системы равно суммарной работе всех сил, действующих на тела этой системы:

∆Eк = Aпот + Aнепот + Aвнеш (1)

Изменение потенциальной энергии системы равно работе потенциальных сил с обратным знаком:

∆Eп = - Aпот (2)

Очевидно, что изменение полной механической энергии равно:

∆E = ∆Eп + ∆Eк (3)

Из уравнений (1-3) получим, что изменение полной механической энергии равно суммарной работе всех внешних сил и внутренних не потенциальных сил.

∆Eк = Aвнеш + Aнепот (4)

Формула (4) представляет из себя закон изменения полной механической энергии системы тел.

В чем состоит закон сохранения механической энергии? Закон сохранения механической энергии состоит в том, что полная механическая энергия замкнутой системы остается неизменной.

 

 

4) Вращательное движение. Момент импульса. Тензор инерции. Кинетическая энергия и момент импульса твёрдого тела. Теоремы Кёнига и Штейнера-Гюйгенса.

Вращательное движение.

Вращательное движение — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной.

При равномерном вращении (T оборотов в секунду),

§ Частота вращения — число оборотов тела в единицу времени.

,

§ Период вращения — время одного полного оборота. Период вращения T и его частота связаны соотношением .

§ Линейная скорость точки, находящейся на расстоянии R от оси вращения

,

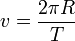§ Угловая скорость вращения тела

.

§ Кинетическая энергия вращательного движения

где I_z — момент инерции тела относительно оси вращения. — угловая скорость

Момент импульса.

Момент импульса характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения.

Момент импульса замкнутой системы сохраняется.

Момент импульса частицы относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:

где — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, — импульс частицы.

Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса):

Производная момента импульса твердого тела по времени равна сумме моментов всех сил, действующих на тело:

.

Тензор инерции.

Тензор инерции — в механике абсолютно твёрдого тела — тензорная величина, связывающая момент импульса тела и кинетическую энергию его вращения с его угловой скоростью:

где — тензор инерции, — угловая скорость, — момент импульса

Кинетическая энергия.

Кинетическая энергия — энергия механической системы, зависящая от скоростей движения её точек. Единица измерения в системе СИ — Джоуль. Кинетическая энергия есть разность между полной энергией системы и её энергией покоя. Часто выделяют кинетическую энергию поступательного и вращательного движения.

Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:

где: 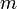— масса тела, — скорость центра масс тела, — момент инерции тела, — угловая скорость тела.

Теорема Кёнига.

Теорема Кёнига позволяет выразить полную кинетическую энергию системы через энергию движения центра масс и энергию движения относительно центра масс.

Кинетическая энергия системы есть энергия движения центра масс плюс энергия движения относительно центра масс:

,

где — полная кинетическая энергия, — энергия движения центра масс, — относительная кинетическая энергия.

Иными словами, полная кинетическая энергия тела или системы тел в сложном движении равна сумме энергии системы в поступательном движении и энергии системы во вращательном движении относительно центра масс.

Теорема Штейнера-Гюйгенса.

Теорема Гюйгенса-Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции этого тела относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями:

Где — известный момент инерции относительно оси, проходящей через центр масс тела, — искомый момент инерции относительно параллельной оси, — масса тела, — расстояние между указанными осями.

 

5) Система двух частиц. Приведённая масса. Центральное поле. Законы Кеплера.

Приведённая масса.

Приведённая масса — условная характеристика распределения масс в движущейся механической системе, зависящая от физических параметров системы (масс, моментов инерции, и др.) и от её закона движения.

Обычно приведенная масса определяется из равенства , где - кинетическая энергия системы, а — скорость той точки системы, к которой приводится масса. В более общем виде приведённая масса является коэффициентом инерции в выражении кинетической энергии системы со стационарными связями, положение которой определяется обобщёнными координатами

где точка означает дифференцирование по времени, а есть функции обобщённых координат.

Система двух частиц.

Задача двух тел состоит в том, чтобы определить движение двух точечных частиц, которые взаимодействуют только друг с другом. Распространённые примеры включают спутник, обращающийся вокруг планеты, планета, обращающаяся вокруг звезды.

Задачу двух тел можно представить как две независимых задачи одного тела, которые привлекают решение для движения одной частицы во внешнем потенциале. Так как многие задачи с одним телом могут быть решены точно, соответствующая задача с двумя телами также может быть решена. В отличие от этого, задача с тремя телами (и, более широко, задача n тел) не может быть решена, кроме специальных случаев.

В задаче двух тел, возникающей, например, в небесной механике или теории рассеяния, приведённая масса появляется как некая эффективная масса, когда задачу двух тел сводят к двум задачам об одном теле. Рассмотрим два тела: одно с массой 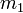и другое с массой . В эквивалентной проблеме одного тела рассматривают движение тела с приведённой массой, равной

где сила, действующая на эту массу, дается силой, действующей между этими двумя телами. Видно, что приведённая масса равна половине среднего гармонического двух масс.

Центральное поле.

Сведя задачу о движении двух тел к задаче о движении одного тела, мы пришли к вопросу об определении движения частицы во внешнем поле, в котором ее потенциальная энергия зависит только от расстояния до определенной неподвижной точки; такое поле называют центральным. Сила

действующая на частицу, по абсолютной величине зависит при этом тоже только от и направлена в каждой точке вдоль радиус-вектора.

При движении в центральном поле сохраняется момент системы относительно центра поля. Для одной частицы это есть

Законы Кеплера.

Законы Кеплера — три эмпирических соотношения. Описывают идеализированную гелиоцентрическую орбиту планеты. В рамках классической механики выводятся из решения задачи двух тел предельным переходом / → 0, где , — массы планеты и Солнца.

1. Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце.

2. Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади.

3. Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет. Справедливо не только для планет, но и для их спутников.

 

6) Функция Лагранжа. Уравнения Лагранжа. Обобщённые импульсы, энергия. Циклические координаты. Фукнция Гамильтона и уравнения Гамильтона.

Функция Лагранжа.

7) Гармонические колебания. Амплитуда. Частота. Пружинный маятник, математический маятник, физический маятник.

Гармонические колебания.

Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:

или

,

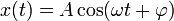где х — значение изменяющейся величины, t — время, остальные параметры — постоянные: А — амплитуда колебаний, ω — циклическая частота колебаний, — полная фаза колебаний, — начальная фаза колебаний.

Обобщенное гармоническое колебание в дифференциальном виде

(Любое нетривиальное решение этого дифференциального уравнения — есть гармоническое колебание с циклической частотой )

§ Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Чтобы свободные колебания были гармоническими, необходимо, чтобы колебательная система была линейной (описывалась линейными уравнениями движения), и в ней отсутствовала диссипация энергии (последняя вызвала бы затухание).

§ Вынужденные колебания совершаются под воздействием внешней периодической силы. Чтобы они были гармоническими, достаточно чтобы колебательная система была линейной (описывалась линейными уравнениями движения), а внешняя сила сама менялась со временем как гармоническое колебание (то есть чтобы зависимость от времени этой силы была синусоидальной).

 

Амплитуда.

Амплитуда — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении. Неотрицательная скалярная величина, размерность которой совпадает с размерностью определяемой физической величины.

Иначе: Амплитуда — модуль максимального отклонения тела от положения равновесия. Например:

§ амплитуда для механического колебания тела (вибрация), для волн на струне или пружине — это расстояние и записывается в единицах длины.

Частота.

Частота — физическая величина, характеристика периодического процесса, равная числу полных циклов процесса, совершённых за единицу времени. Стандартные обозначения в формулах — , , или . Единицей частоты в СИ в общем случае является Гц. Величина, обратная частоте, называется периодом.

В природе известны периодические процессы с частотами от ~10⁻¹⁶ Гц (частота обращения Солнца вокруг центра Галактики) до ~10³⁵ Гц (частота колебаний поля, характерная для наиболее высокоэнергичных космических лучей).

Пружинный маятник.

Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.

Когда на массивное тело действует упругая сила, возвращающая его в положение равновесия, оно совершает колебания около этого положения. Такое тело называют пружинным маятником. Колебания возникают под действием внешней силы. Колебания, которые продолжаются после того, как внешняя сила перестала действовать, называют свободными. Колебания, обусловленные действием внешней силы, называют вынужденными. При этом сама сила называется вынуждающей.

В простейшем случае пружинный маятник представляет собой движущееся по горизонтальной плоскости твердое тело, прикрепленное пружиной к стене.

Математический маятник.

Математический маятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен

и не зависит от амплитуды и массы маятника.

Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.

При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной.

Физический маятник.

Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.

8) Колебания с трением. Диссипативная функция.

В реальных системах всегда происходит диссипация энергии. Если потери энергии не будут компенсироваться за счет внешних устройств, то колебания с течением времени будут затухать и через какое-то время прекратятся вообще. Рассмотрим колебания пружинного маятника в вязкой среде.

Для тела, движущегося в однородной вязкой среде, сила трения зависит только от скорости. При малых скоростях можно считать, что сила трения

, где бета – положительный постоянный коэффициент.

С учётом силы трения уравнение свободных колебаний пружинного маятника принимает вид:

, где б – коэффициент затухания.

На рис. 1 приведена зависимость амплитуды колебаний от времени при различных соотношениях между параметрами и .

Рис. 1. Зависимостьпри различных соотношениях между собственной частотой и коэффициентом затухания .

Очень часто "качество" колебательной системы характеризуют безразмерным параметром , называемым добротностью. Добротность пропорциональна отношению запасенной энергии к энергии теряемой за период [3]:

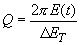
(6)

В случае слабого затухания () зависимость полной энергии от времени выражается в виде

(7)

где – начальное значение полной энергии осциллятора. Тогда в соответствие с формулами (6) и (7)

(8)

Таким образом, добротность характеризует скорости превращения энергии в колебательной системе. С другой стороны по порядку величины это есть не что иное, как число колебаний, совершаемых системой за характерное время их затухания . Следует отметить, что добротность не только характеризует затухание колебаний, но и является важной величиной, определяющей параметры вынужденных колебаний, осуществляемых под действием внешней периодической силы (см. пункт 2.3.3).

Выводы.

· Характер собственных колебаний при наличии силы трения определяется соотношением между и . При – апериодический режим (3); – колебания описываются периодическим законом c экспоненциально убывающей от времени амплитудой (4); – режим критического затухания (5).

· Добротность колебательной системы является очень важным параметром, характеризующим диссипационные процессы в системе.

Диссипативная функция (функция рассеяния) — функция, вводимая для учёта перехода энергии упорядоченного движения в энергию неупорядоченного движения, в конечном счёте — в тепловую, например, для учёта влияния сил вязкого трения на движение механической системы. Диссипативная функция характеризует степень убывания механической энергии этой системы. Диссипативная функция, делённая на абсолютную[1] температуру, определяет скорость, с которой возрастает энтропия в системе (т. н. производство энтропии). Диссипативная функция имеет размерность мощности.

 

9) Вынужденные колебания без трения. Биения. Резонанс.