Несобственные интегралы от неограниченных функций

Несобственные интегралы

 

Вводя определенный интеграл как предел интеграль­ных сумм, мы предполагали, что отрезок интегрирова­ния конечный, а подынтегральная функция ограничена на этом отрезке. Если хотя бы одно из этих условий не выполнено, то данное выше определение определенного интеграла теряет смысл. Так, в случае бесконечного от­резка интегрирования нельзя разбить отрезок на п ча­стей конечной длины, а в случае неограниченной функ­ции интегральная сумма не имеет конечного предела. Однако и в этих случаях удается обобщить понятие оп­ределенного интеграла. В результате такого обобщения и появилось понятие несобственного интеграла.

Несобственные интегралы с бесконечными преде­лами интегрирования

Определение. Пусть функция 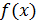определена в промежутке 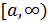и интегрируема в любой его ча­сти 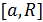, т. е. существует определенный интеграл при любом 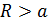. Тогда, если существует конечный предел

то его называют несобственным интегралом первого ро­да и обозначают символом

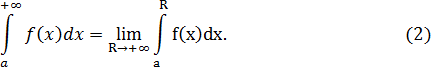
В этом случае говорят, что интеграл (2) существует или сходится. Если же предел (1) не существует или бесконечен, то говорят, что несобственный интеграл не существует или расходится.

Аналогично интегралу (2) вводится несобственный интеграл вида

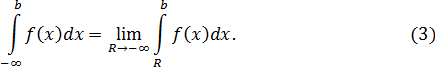
Наконец, как сумму подобных интегралов можно оп­ределить несобственный интеграл с обоими бесконеч­ными пределами, т. е. определить его равенством

где 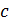— любое число; при условии существования обо­их интегралов справа,

Легко установить геометрический смысл несобствен­ного интеграла первого рода. Пусть 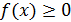. Тогда, если определенный интеграл

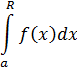
выражает площадь области, ограниченной сверху графиком функции 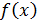, снизу осью 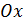, слева прямой 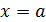, справа прямой 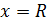, то естественно считать, что несобственный интеграл

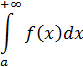
выражает конечную площадь бесконечной области, ограниченной снизу осью 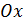, сверху графиком функции 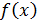, слева прямой 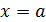(см. рис.).

Аналогич­ные рассуждения имеют место для интегралов (3) и (4).

Рассмотрим несколько примеров несобственных ин­тегралов первого рода.

Пример 1.

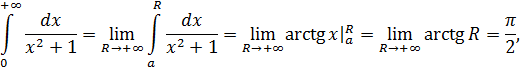
т. е. данный интеграл сходится.

Пример 2.

а предел функции при не существует, следовательно, интеграл расходится.

Заметим, что в рассмотренных примерах само вы­числение несобственного интеграла основано на его определении.

Несобственные интегралы от неограниченных функций

Определение. Пусть функция 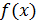определена в промежутке 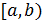. Точку 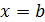будем называть осо­бой, если функция 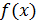не ограничена в окрестности этой точки, но ограничена на любом 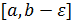, заклю­ченном в 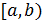(см. рис.).

Предполагается, что на лю­бом 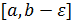, функция 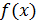интегрируема. Тогда, как бы ни было мало 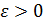, если существует конечный пре­дел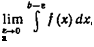

то его называют несобственным интегралом второго ро­да и обозначают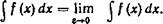

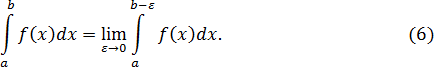
В этом случае говорят, что интеграл (6) существует или сходится. Если же предел (5) не существует или бесконечен, то говорят, что интеграл (6) не существует или расходится.

Аналогично, если точка 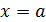— особая точка, то несобственный интеграл в этом случае определяется так:

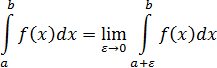
Если 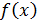не ограничена в окрестности какой-нибудь внутренней точки 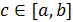, то по определению по­лагают

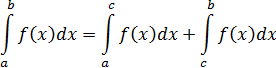
при условии существования обоих интегралов справа.

Наконец, если и — особые точки, то в этом слу­чае несобственный интеграл определяется как сумма

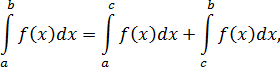
где 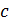— любая точка из 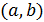, если оба интеграла справа существуют.

Пример.

а при

таким образом, данный интеграл сходится при 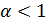и расходится при .

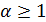Признаки сходимости несобственных интегралов. Рассмотрим вопрос сходимости интегралов с бесконечными пределами интегрирования вида

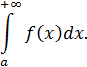
Аналогичные рассуждения можно провести и для интегралов других видов.

Следующая теорема познакомит нас с одним из признаков сходимости несобственных интегралов.

Теорема 11 (признак сравнения несобственных интегралов). Если функции и 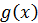непрерывны на полуинтервале 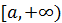и удовлетворяют на нем усло­вию , то из сходимости интеграла

следует сходимость интеграла

а из расходимости интеграла (8) следует расходимость интеграла (7).

Доказательство. Так как интеграл (7) по ус­ловию сходится, то согласно теореме об ограниченности сходящейся последовательности (сходящаяся последовательность ограничена) это означает, что существует число 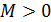такое, что для любого 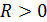выполняется неравенство

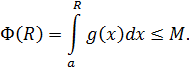
Тогда, в силу данного условия и оценки 2°

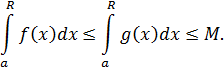
А это означает, что функция

Монотонно возрастает и ограничена, т. е. имеет конечный предел при , и, следовательно, интеграл (8) сходится.

Если же (8) расходится, то, допустив сходимость интеграла (7), получим по только что доказанному схо­димость интеграла (8), что противоречит условию. Окончательно получаем, что интеграл (7) также расхо­дится.

Замечание. Что касается сходимости несобствен­ных интегралов второго рода, то теория этих интегралов аналогична теории несобственных интегралов первого рода. В частности, признак сравнения для таких инте­гралов можно сформулировать следующим образом: ес­ли функци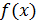и и 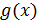непрерывны на полуинтервале 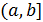и для всех точек 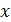в некоторой окрестности точки а выполняются условия 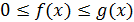, то из сходимости интеграла 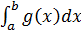следует сходимость интеграла 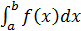, а из расходимости 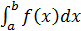следует расходимость .

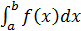Пример. Исследовать сходимость

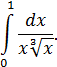
Специальный признак сходимости. Если 1) функция 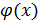монотонно стремится к 0 при 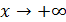и 2) функция 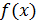имеет ограниченную первообразную

то интеграл

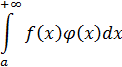
сходится, вообще говоря. не абсолютно.

В частности, интегралы

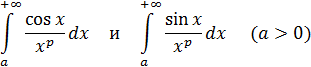
сходятся, если 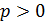.