Сервисами робота называется величина линейных, угловых, пространственных и объёмных перемещений, в пределах которых схват выполняет манипуляции с изделиями. Различают линейный L, угловой a, плоскостной Н и объёмный V сервис.
Различают линейный сервис по осям координат x, y, z – lx, ly, lz. Угловой сервис характеризует перемещения схвата в манипуляторах, работающих в цилиндрической, сферической и комбинированной системах координат. Плоскостной сервис соответствует рабочей зоне, а объёмный – рабочему объёму.
Сервис является качественной характеристикой манипулятора. Для сравнительной оценки манипуляторов пользуются коэффициентами линейного, углового, пространственного и объёмного сервиса, значения которых определяются соответственно из соотношений:
 , (13)
, (13)
где  - величины линейного, углового, пространственного и объёмного сервиса;
- величины линейного, углового, пространственного и объёмного сервиса;
L – величина линейного перемещения относительно начала базовой системы координат или полный линейный сервис;
S, V – площадь зоны и объём, описываемые схватом относительно начала базовой системы координат или полный плоскостной и объёмный сервисы.
Значения коэффициентов сервиса могут изменяться от нуля (в начальных точках и на границе рабочей зоны и объёма) до единицы при полном сервисе. Максимальные значения коэффициентов сервиса находятся с учётом средних значений Сaср; Сlср; СSср; СVср из выражений:
 (14)
(14)
где dl, da, ds, dυ – элементарные значения величин L, a, S, V.
При проектировании манипуляторов следует стремиться к оптимальным значениям коэффициентов сервиса, добиваясь соразмерных и гармонизирующих перемещений звеньев и схвата.
Определение зоны обслуживания, величины и коэффициента сервиса
|
|
Манипуляторов
Структура и число степеней свободы кинематических пар манипулятора обуславливает его зону обслуживания, вид, величину и коэффициент сервиса. Для манипулятора со структурой Р(3,2), когда его последнее звено образует с кистью кинематические пары различной подвижности определим перечисленные характеристики.
1. Вращательная пара, образованная последним звеном кинематической цепи манипулятора с кистью, обеспечивает движение схвата двух основных видов, когда ось совпадает (или коллинеарна) с осью кинематической пары или расположена в плоскости, перпендикулярной (или направленной под любым углом больше 0) к оси пары. Соответственно движение схвата характеризуется или углом поворота  относительно собственной оси или углом поворота j в плоскости, наклонённой или перпендикулярной к оси пары.
относительно собственной оси или углом поворота j в плоскости, наклонённой или перпендикулярной к оси пары.
Углом сервиса является максимальный угол поворота схвата, отсчитываемый от начальной точки или оси, в пределах которого он может поворачиваться при данной структуре, составе кинематических пар, их расположении и размерах звеньев манипулятора. Максимальные значения углов поворота a и j являются соответственно осевым и плоскостным углами сервиса. При определении a и j считают, что схват не покидает исходной точки Д рабочей зоны при различных движениях кисти.
Первый случай.

 Структура манипулятора (рис. 9) описывается выражением Р(3,2).
Структура манипулятора (рис. 9) описывается выражением Р(3,2).
В системе координат манипулятор располагается таким образом, что ось кисти совпадает (или коллинеарна) с осью Ox, а стойка находится в начале координат.
|
|
Схват может поворачиваться на угол a вокруг своей оси.
Этот угол является осевым углом сервиса. Отношение
 (15)
(15)
называется коэффициентом осевого сервиса схвата. 0£Сa£1. Сa= 0 при неподвижном схвате или в точке начала вращения, Сa= 1 при его полном обороте или при вращении.
При соосном последовательном расположении вращательных пар суммарный сервис схвата
 ,
,
где a и j - углы поворота кисти и последнего звена. Знак (+) соответствует однонаправленному, а (-) разнонаправленному повороту.
 (16)
(16)
Соосное расположение вращательных пар позволяет увеличить или уменьшить осевой сервис схвата.
Второй случай.

 |
Ось схвата перпендикулярна оси вращения пары, которая направлена вдоль оси Oy (рис. 10). Это ограничение обуславливает движение схвата и звеньев в плоскости F, параллельной XOZ. Манипулятор имеет ту же структуру, что и в первом случае. Движение схвата характеризуется углом сервиса j в плоскости, перпендикулярной оси OY.
Поместим в точку Д (центр схвата) вращательную пару (рис. 11), ось которой параллельна оси OY, такую же пару поместим в точку С. Соединим точку Д и А и обозначим переменное расстояние АД через R. Фигура АВСД представляет шарнирный четырёхзвенник, длина звеньев l1,l2,l3 которого соответствует длине плеча, предплечья и кисти манипулятора.
Зоной обслуживания (или рабочей зоной) F является геометрическое место точек совпадающих с положением центра схвата Д, в пределах которого можно выполнять данную, характеризуемую положением схвата, по отношению к объекту манипулирования, операцию. Зона обслуживания представляет отрезок вдоль прямой АД. Уголом сервиса j является угол движения звеньев манипулятора в плоскости F, равный максимальному углу, отсчитываемому от линии АД, в диапазоне которого может поворачиваться схват при данном значении R.
|
|
Для нахождения j проведём линию АС. Из треугольников АВС и АДС следует:
 (17)
(17)
Решив систему уравнений относительно cosj, получим
 (18)
(18)
где g - угол между плечом l1 и предплечьем l2 манипулятора.
Коэффициент сервиса Сj в плоскости движения схвата:
 (19)
(19)
Манипулятор может занимать положение АВ1С1Д1, симметричное относительно оси ОY. Симметричное отображение имеют угол сервиса j1 и зона обслуживания R1.
Схват может совершать относительно точки Д полный оборот и качаться. В первом случае имеет место кривошипно-коромысловый механизм с кривошипом СД и коромыслом АВ, угол сервиса jmax =2 p, а Сj= 1, во втором – двухкоромысловый механизм с коромыслами АВ и СД, угол сервиса amax <2 p, а  . Установим, каким соотношениям должны удовлетворять размеры звеньев и кисти манипулятора l1, l2, l3 для получения заданного значения Сj.
. Установим, каким соотношениям должны удовлетворять размеры звеньев и кисти манипулятора l1, l2, l3 для получения заданного значения Сj.
В основе манипулятора лежит шарнирный четырехзвенник АВСД. Задача определения зоны обслуживания, в которой коэффициент сервиса Сj равен единице, сводится к определению длины стойки R кривошипно-коромыслового механизма, исходя из условия существования кривошипа (условия Грасгофа). Обычно в манипуляторах звено АВ совершает качательное движение, то есть в шарнирном четырёхзвеннике оно является коромыслом. Поэтому для того чтобы Сj =1, манипулятор должен представлять кривошипно-коромысловый механизм, причём минимальным звеном является кривошип l3. наибольшим звеном может быть одно из трёх звеньев: стойка R, коромысло l1, шатун l2. согласно условию существования кривошипа сумма длин наибольшего и наименьшего звеньев должна быть меньше или равна сумме длин двух других звеньев. Исходя из этого, возможны следующие три варианта существования кривошипа в кривошипно-коромысловом механизме манипулятора:
R+l3 £ l1+l2; (20)
l1+l3 £ R+l2; (21)
l2+l3 £ l1+R. (22)
Из выражения (20) получим наибольшую длину стойки Rmax, удовлетворяющую условию существования кривошипа:
Rmax=l1+l2-l3 (23)
Из выражений (21) и (22) находим минимальную длину стойки:
Rmin=|l1-l2|+l3 (24)
Зона обслуживания манипулятора при Сj= 1 и l1³l2 представляет прямую линию и равна разности между наибольшим Rmax и наименьшим Rmin значениями стойки:
Lоб=Rmax-Rmin=2(l2-l3) (25)
Зона обслуживания на рис.10 обозначена I. Из выражения (25) следует: для увеличения зоны обслуживания манипулятора, содержащего вращательные пары, следует увеличить длину шатуна l2 и уменьшить длину l3 кисти.
Рассмотрим случай, когда схват совершает качательные движения, то есть Сj< 1. для этого увеличим Rmax. В результате получаем двухкоромысловый механизм, в котором звено СД совершает лишь часть оборота вокруг точки Д. предельное увеличение R соответствует случаю, когда коромысло l1, шатун l2 и коромысло l3 вытянуты в одну линию:
Rпр=l1+l2+l3 (26)
Этому предельному значению соответствует коэффициент сервиса Сj =0. зона обслуживания манипулятора, выполненного на базе двухкоромыслового механизма:
Lоб=Rпр-Rmax =(l1+l2+l3)- (l1+l2-l3)=2l3 (27)
Таким образом, зона обслуживания равна удельной длину кисти l3 и обозначена II.
Другое предельное положение манипулятора соответствует расположению коромысла l1, шатуна l2 и коромысла l3 в линию, но в противоположном направлении. Длина стойки R при этом уменьшается до величины:
R0= l3-|l1-l2| (28)
Зона обслуживания представляет линию III
Lо=Rmin-Ro =2(l1-l2) (29)
Коэффициент сервиса в этом случае равен нулю. Максимальный угол сервиса jmax, в пределах которого может повернуться звено СД при данном R, определяется из выражения (18) при значениях g =180° и g =360°, что соответствует крайним положениям механизма:
 (30)
(30)
Верхние знаки соответствуют зоне II, а нижние – III. Для зоны I угол сервиса jmax=p (определяется путём подстановки в выражение (18) выражения (23) и g =180°).
2. Сферическая пара с пальцем. Кисть манипулятора с его последним звеном образует двухподвижную пару. l1, l2, l3, R остаются теми же, что и в предыдущем случае. Ось пальца параллельна оси OY, а ось прорези направлена по оси OZ.
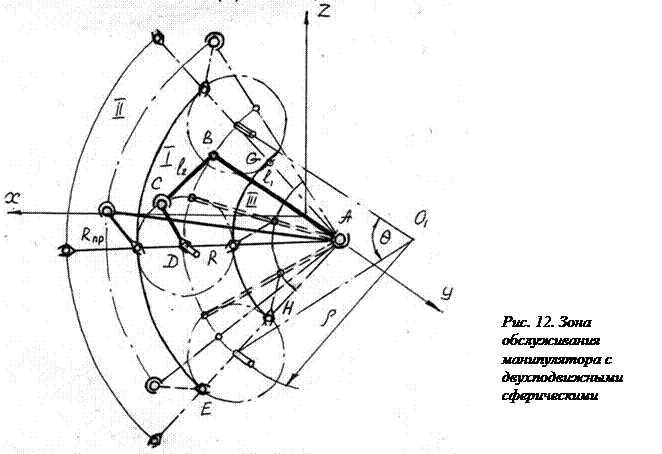
Зона обслуживания манипулятора с двухподвижными сферическими парами характеризуется двумя сервисами: углом сервиса j движения схвата в плоскости F (как для вращательной пары) и углом сервиса q, обусловленного размерами прорези в паре. Отношение
 (31)
(31)
является коэффициентом сервиса в плоскости прорези пары. Зона обслуживания представляет собой фигуру в форме кольца:
а) для манипулятора, выполненного на базе кривошипно-коромыслового механизма с jmax=p
 (32)
(32)
б) для манипулятора, выполненного на базе двухкоромыслового механизма (рис. 12), имеется две предельных зоны:
 (33)
(33)
Произведение угловых коэффициентов Сj и Сq является коэффициентом сервиса двухподвижной сферической пары
 (34)
(34)
величина которого изменяется в пределах 0£ С £1.
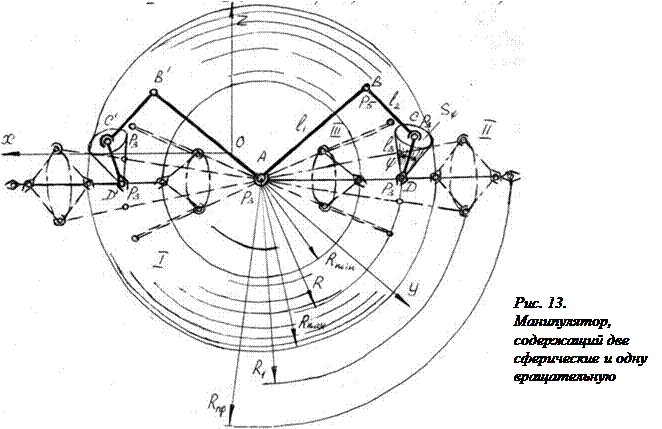
3. Трёхподвижная сферическая пара. Манипулятор содержит сферические пары А, С и вращательную В (рис. 13). Схват вращается вокруг точки Д (центра схвата), в которой помещена трёхподвижная сферическая пара. Манипулятор представляет собой пространственный механизм АВСД. Для получения зоны обслуживания манипулятора следует вращать плоский четырёхзвенный механизм относительно стойки АД. В результате вращения трём зонам плоского манипулятора соответствуют три зоны обслуживания пространственного манипулятора. Зона I имеет форму шара, а зона II и III – шарового сектора, сферическая поверхность которого
 . (35)
. (35)
Угол сервиса y определяется как телесный угол, заключенный между всеми возможными положениями кисти СД. За меру y телесного угла с вершиной в центре схвата Д принимается отношение площади, вырезаемой телесным углом на поверхности шара, описанного радиусом СД, равным длине кисти l3, из центра Д, к квадрату радиуса этого шара:
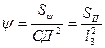
Максимальная величина угла сервиса равна отношению площади всего шара, который описывает кисть манипулятора, к квадрату её длины:
 (36)
(36)
Отношение фактического угла сервиса к максимально возможному его значению называется коэффициентом сервиса в данной точке:
 (37)
(37)
Подставляя значения, получим коэффициент сервиса Сy пространственного манипулятора при данном значении R
 где верхние знаки для зоны II, а нижние – для зоны III. Для зоны I коэффициент сервиса Сy= 1.
где верхние знаки для зоны II, а нижние – для зоны III. Для зоны I коэффициент сервиса Сy= 1.