Преобразования координат
Некоторые сведения о системах координат
 |
Декартовыми прямоугольными координатами точки Р называются взятые с определённым знаком расстояния этой точки до трёх взаимно перпендикулярных плоскостей или, что то же самое, проекции радиус-вектора точки Р на три взаимно перпендикулярные координатные оси. В зависимости от взаимного расположения положительных направлений координатных осей возможна правая (рис. 17, а) и левая (рис. 17, б) координатные системы.
В геометрических и кинематических исследованиях манипуляторов применяются правые прямоугольные, цилиндрические и сферические системы координат.
Более общую систему координат получают, задавая какие-либо семейства координатных поверхностей, таких, что через каждую точку пространства проходит по одной такой поверхности каждого семейства. Положения точки в такой системе определяется значениями параметров координатных поверхностей, проходящих через эту точку. Наиболее употребительные системы криволинейных координат – цилиндрическая и сферическая.
Цилиндрические координаты (рис. 18): r и j - полярные координаты проекции точки Р на основную плоскость (обычно XOY); z – аппликата - расстояние от точки Р доя основной плоскости. Для цилиндрических координат координатными поверхностями являются плоскости, перпендикулярные к оси Z (z=const); полуплоскости, ограниченные осью Z (j=const), и цилиндрические поверхности, осью которых является ось Z (r=const). Координатные линии – линии пересечения этих поверхностей.
Сферические координаты (R – длина радиус-вектора, j - долгота, q - полярное расстояние) представлены на рис. 19. Если давать сферическим координатам значения в следующих пределах: 
, 
, 
, то получаются однозначно все точки пространства. Координатные поверхности – это сферы с центром в начале (R=const), полуплоскости, ограниченные осью Z (j=const), конусы (с вершиной в начале), для которых ось Z является осью (q=const). Координатные линии это линии пересечения этих поверхностей.
Связь между прямоугольными, цилиндрическими и сферическими координатами представлена в таблице формулами перехода, которые справедливы при следующих допущениях:
а) начала координат прямоугольной, цилиндрической и сферической систем совпадают: основная плоскость (Z=0) прямоугольной и цилиндрической систем совпадает с основной плоскостью (q=0) сферической системы; линии отсчёта (j=0)сферической и цилиндрической систем совпадают с осью х=0 прямоугольной системы. Оси OZ прямоугольной и цилиндрической систем совпадают;
б) отсчёт положительных значений j производится против часовой стрелки, если смотреть с положительного направления оси OY. Знак соответствует знаку координаты по оси OY.
Таблица 5
Связь между прямоугольными, цилиндрическими и сферическими
Координатами
| Система координат | Система координат | ||
| Прямоугольная (x,y,z) | Цилиндрическая (r,j,z) | Сферическая (R,j,q) | |
| Прямоугольная (x,y,z) | x=x y=y z=z | 
| 
|
| Цилиндрическая (r,j,z) | 
| r=r j=j z=z |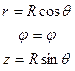 
|
| Сферическая (R,j,q) | 
| 
| R=R j=j q=q |
Направление в пространстве характеризуется единичным вектором 
или его координатами – косинусами углов (рис. 20), образованных заданными направлениями с положительными направлениями осей координат (направляющие косинусы); при этом
l=cosa; m=cosb; n=cosg; l2+m2+n2=1
Угол j между двумя заданными направлениями с направляющими косинусами l1; m1; n1 и l2; m2; n2 определяется из выражения cosj= l1l2+ m1m2+ n1n2
Если два направления перпендикулярны, то l1l2+ m1m2+ n1n2=0.
Переход от одной прямоугольной системы координат к другой прямоугольной системе координат можно осуществить при помощи параллельного переноса (до совмещения начала координат) и поворота системы относительно начала (до совмещения осей). Поворот прямоугольной системы координат можно описать с помощью направляющих косинусов, углов Эйлера, вектора конечного поворота, параметров Родрига-Гемильтона, параметров Кэли-Клейна и др.